10.6二维振动的合成 10.6二维振动的合成 频率比1:21:31:42:3 20 ·●●川:‖全同 振幅调节 频率调节 初相调节 显示控制动画控制 前页后页目录 1
前页 后页 目录 1 10.6 二维振动的合成 10.6 二维振动的合成

10.6二维振动的合成 一.两个同频率、相互垂直的简谐振动合成 x=A cos(@t+o) y=A2 cos(@t+0) 消去t,得 -2xy 4承8A4 c0s(20-4o)=sin2(20-4o) 合运动一般不是简谐振动 前页后页且录2
前页 后页 目录 2 10.6 二维振动的合成 一 . 两个同频率、相互垂直的谐振动合成 消去t,得 2 2 2 2 2 20 10 20 10 1 2 1 2 2 cos( ) sin ( ) x y x y A A A A + − − = − A1 A2 y x 合运动一般不是简谐振动 1 10 x A t = + cos( ) 2 20 y A t = + cos( ) 一. 两个同频率、相互垂直的简谐振动合成
10.6二维振动的合成 几种特例 (1)40-410=0时 △中=0 y= A △中= △中= (2)40一410=元时 4=3 y--4x 一般 合运动是简谐振动。 s=x2+y2=A2+A cos(@t+) 前页后页目录3
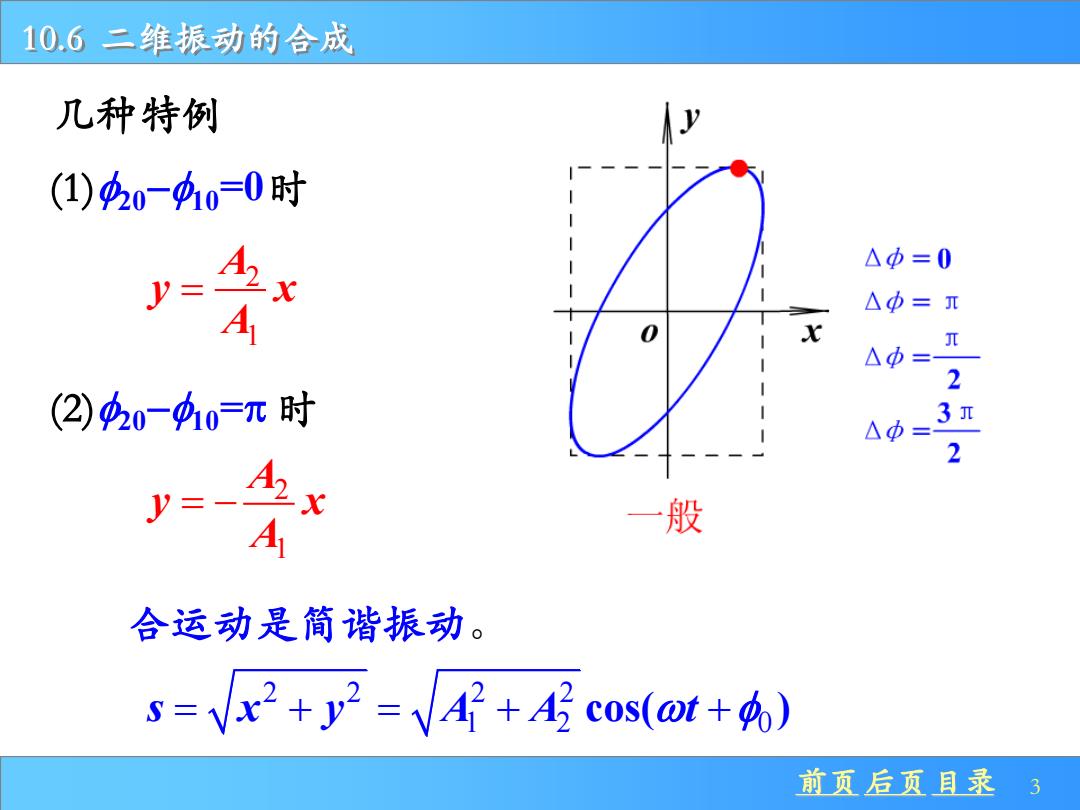
前页 后页 目录 3 10.6 二维振动的合成 几种特例 (1)20−10=0时 2 1 A y x A = (2)20−10=p 时 2 1 A y x A = − 合运动是简谐振动。 2 2 2 2 1 2 0 s x y A A t = + = + + cos( )

10.6二维振动的合成 (3)中0-410=元/2时 4R4 △中=0 △中= (4)20一410=3π/2时 △= x2,y2 4功=3n 1 一般 合运动轨道是正椭圆或圆。非简谐振动 前页后页目录 4
前页 后页 目录 4 10.6 二维振动的合成 (3)20−10=p/2时 2 2 2 2 1 2 1 x y A A + = (4)20−10=3p/2时 2 2 2 2 1 2 1 x y A A + = 合运动轨道是正椭圆或圆。非简谐振动
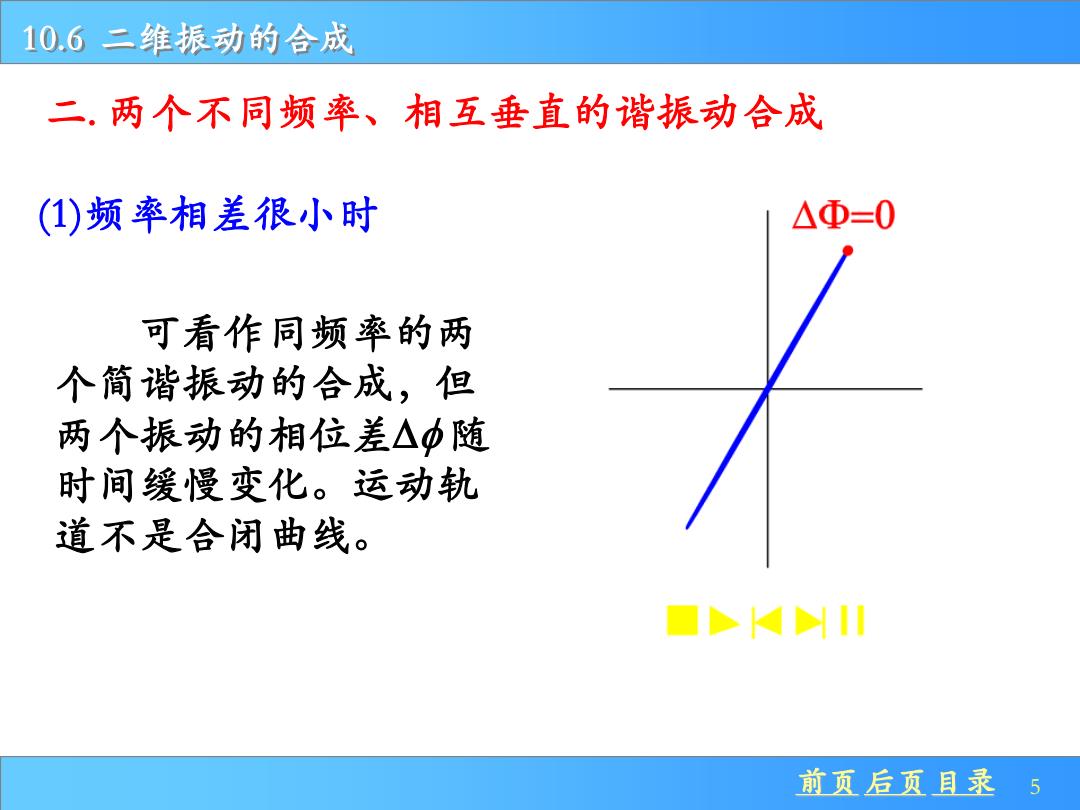
10.6二维振动的合成 二.两个不同频率、相互垂直的谐振动合成 (1)频率相差很小时 △Φ=0 可看作同频率的两 个简谐振动的合成,但 两个振动的相位差△中随 时间缓慢变化。运动轨 道不是合闭曲线。 □b4HII 前页后页目录 5
前页 后页 目录 5 10.6 二维振动的合成 二. 两个不同频率、相互垂直的谐振动合成 (1)频率相差很小时 可看作同频率的两 个简谐振动的合成,但 两个振动的相位差D 随 时间缓慢变化。运动轨 道不是合闭曲线

10.6三维振动的合成 (②)频率成简单的整数比 合成运动通常有 稳定的闭合轨迹,称 2:1y中-0中02 为李萨如图形。 应用: 测定频率或相位差。 3:1 3:2 典型的李萨如图形 本节完 前页后页目录 6
前页 后页 目录 6 10.6 二维振动的合成 典型的李萨如图形 (2)频率成简单的整数比 合成运动通常有 稳定的闭合轨迹,称 为李萨如图形。 应用: 测定频率或相位差。 本节完