
10.1谐振动 10.1谐振动 振动:物体在某一位置附近来回往复的运动。 以质点平衡位置为坐标原点, 沿质点运动方向为x轴。 0 当合力F=-i,质点作简谐振动 运动方程 x=Acos(at+) A,0,中均为常数 前页后页目录 1
前页 后页 目录 1 10.1 谐振动 10.1 谐振动 当合力 以质点平衡位置为坐标原点, F kxi ˆ = − 沿质点运动方向为x轴。 o x ,质点作简谐振动 运动方程 0 x A t = + cos( ) A, , 0 均为常数 振动:物体在某一位置附近来回往复的运动

10.1谐振动 一.谐振动的特征及其表达式 弹簧振子 HWo 一端固定的轻弹簧,另一端 与质点相连的系统。 水平放置的弹簧振子沿水平 方向的自由振动是简谐振动。 竖直放置的弹簧振子沿竖直 FM 方向的自由振动也是简谐振动。 前页后页目录 2
前页 后页 目录 2 10.1 谐振动 弹簧振子 一. 谐振动的特征及其表达式 水平放置的弹簧振子沿水平 方向的自由振动是简谐振动。 竖直放置的弹簧振子沿竖直 方向的自由振动也是简谐振动。 一端固定的轻弹簧,另一端 与质点相连的系统

10.1谐振动 弹簧振子简谐振动的运动方程 沿质点运动方向为x轴, 平衡位置为坐标原,点0。 .0 由胡克定律,弹力f=x 合力 F=-koxi Fx=-kx 由牛顿第二定律4x= d2x -kx dt2 m 前页后页目录 3
前页 后页 目录 3 10.1 谐振动 沿质点运动方向为x轴, x o 合力 由牛顿第二定律 弹簧振子简谐振动的运动方程 F kxi ˆ = − F kx x = − x x F a m = 2 2 d d x t x x F F m = 由胡克定律,弹力 f kx = −kx 平衡位置为坐标原点o

10.1谐振动 d2x -kx dr2 m d2x 令0= ,则 =-02x m dr2 d2x dr2+@'x=0 方程的解x=Ac0s(ot+中) 或x=Asin(ot+) 0称为固有角频率 A和,由其它已知条件确定 前页后页目录4
前页 后页 目录 4 10.1 谐振动 或 方程的解 或 称为固有角频率 令 ,则 k m = 2 2 2 d d x x t = − 2 2 0 2 d d x x t + = 0 x A t = + cos( ) 0 x A t = + sin( ) 2 2 d d x kx t m − = A和0由其它已知条件 确定

10.1谐振动 由初始条件确定振幅、初相位 x=Acos(@t+) v=dr dt =-A@sin(ot+φo) 初始条件:t=0时,x=X0及0=V0 xo=Acoso vo=-@Asingo arctan 由条件决定第几象限 其它条件定振幅、初相位 x1=Acos(@+) 如t=t1时,x=X1及0=01 v=-@Asin(@t+o) 前页后页目录5
前页 后页 目录 5 10.1 谐振动 初始条件:t =0时,x=x0及v=v0 由条件决定第几象限 0 0 x A = cos 0 0 v = − Asin 2 2 0 0 A x ( ) = + v 0 0 0 arctan x − = v 如t =t1时,x=x1及v=v1 0 x A t = + cos( ) d d x t v = 由初始条件确定振幅、初相位 其它条件定振幅、初相位 1 1 0 x A t = + cos( ) 1 1 0 v = − + A t sin( ) 0 = − + A t sin( )

10.1谐振动 谐振动的特征: (1)合外力为线性回复力F=-k (2)加速度与位移成正比且反向 dt2 =-02x (3)位移是时间的余弦函数x=Ac0s(ot+) 简谐振动的速度 速度最大值 v=dr =-@Asin(@t+o) Um =@A dt 简谐振动的加速度 加速度最大值 d2x Q= dr2 =-02Ac0s(ot+4) 0m=02A 前页后页目录 6
前页 后页 目录 6 10.1 谐振动 谐振动的特征: (1)合外力为线性回复力 (2)加速度与位移成正比且反向 F kx x = − 2 2 2 d d x x t = − (3)位移是时间的余弦函数 0 x A t = + cos( ) 简谐振动的速度 d d x t v = 0 = − + A t sin( ) 简谐振动的加速度 2 2 d d x a t = 2 0 = − + A t cos( ) vm =A 2 a A m = 加速度最大值 速度最大值

10.1谐振动 二.描述谐振动的特征量 x=Acos(at+) 1)振幅4 SI制:m(米) 质点离开平衡位置的最大位移的绝对值。 2)周期T SI制:s(秒) 完成一次完整振动所经历的时间。 x=Acos(@t+)=Acos[@(T+t)+] oT=2元 T=2n 0 前页后页目录7
前页 后页 目录 7 10.1 谐振动 1)振幅A 2)周期T 0 x A t = + cos( ) 0 = + + A T t cos[ ( ) ] T = 2π 2π T = A A o x 二. 描述谐振动的特征量 0 x A t = + cos( ) 质点离开平衡位置的最大位移的绝对值。 SI制:m(米) 完成一次完整振动所经历的时间。 SI制:s(秒)

10.1谐振动 3)频率y SI制:Hz(赫兹) 单位时间内完成的完整振动的次数。 10 T2π 4圆频率0 SI制:rad/s(孤度/秒) 2π单位时间内完成的完整振动的次数。 2π 0=2πy= 前页后页目录 8
前页 后页 目录 8 10.1 谐振动 3)频率n 1 T n = 2π = 4)圆频率 n = 2π 单位时间内完成的完整振动的次数。 SI制:Hz(赫兹) 2单位时间内完成的完整振动的次数。 SI制:rad/s(弧度/秒) 2π T =

10.1谐振动 简谐振动表达式 x=Acos(@t+) 2 x=Acos t+% x=Ac0s(2πvt+4) 5)相位中 0t+央-2开1+质=2m1t负 决定简谐振动质点的运动状态。 初相 t=0时刻的相位。 前页后页目录 9
前页 后页 目录 9 10.1 谐振动 简谐振动表达式 5)相位 0 = +t 初相0 0 x A t = + cos( ) 0 2π x A t cos T = + x A t = + cos(2πn 0 ) 0 2π t T = + 0 = + 2πn t 决定简谐振动质点的运动状态。 t =0时刻的相位
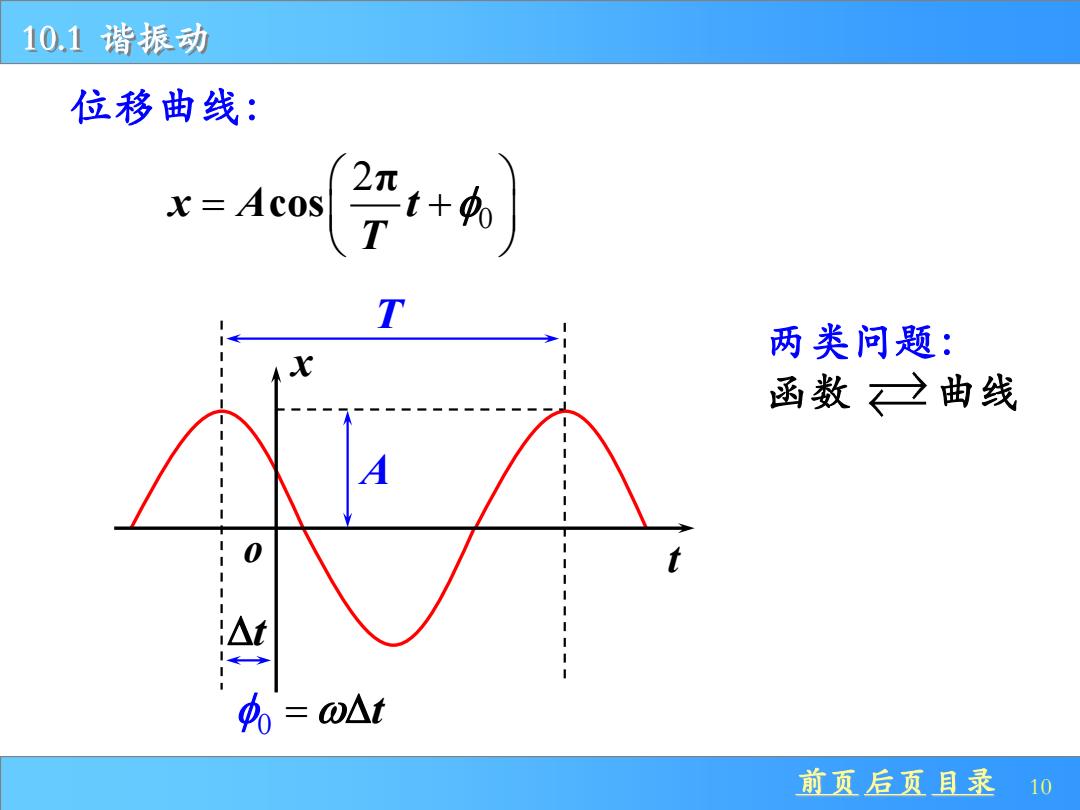
10.1谐振动 位移曲线: x=Acos 2 -t+o 两类问题: 函数之曲线 %=0△t 前页后页目录10
前页 后页 目录 10 10.1 谐振动 位移曲线: A o x t T 0 =t t 两类问题: 函数 曲线 0 2π x A t cos T = +