8.3毕奥一萨伐尔定律 8.3毕奥一萨伐尔定律 一.毕奥一萨伐尔定律 电流元在P,点激发的磁感应强度 dB dB=凸Idixe, e 4πr2 dB 大小: dB=o Idlsina 4π r2 方向: Idl xe, 真空中的磁导率:4=4π×107NA-2 前页后页目录 1
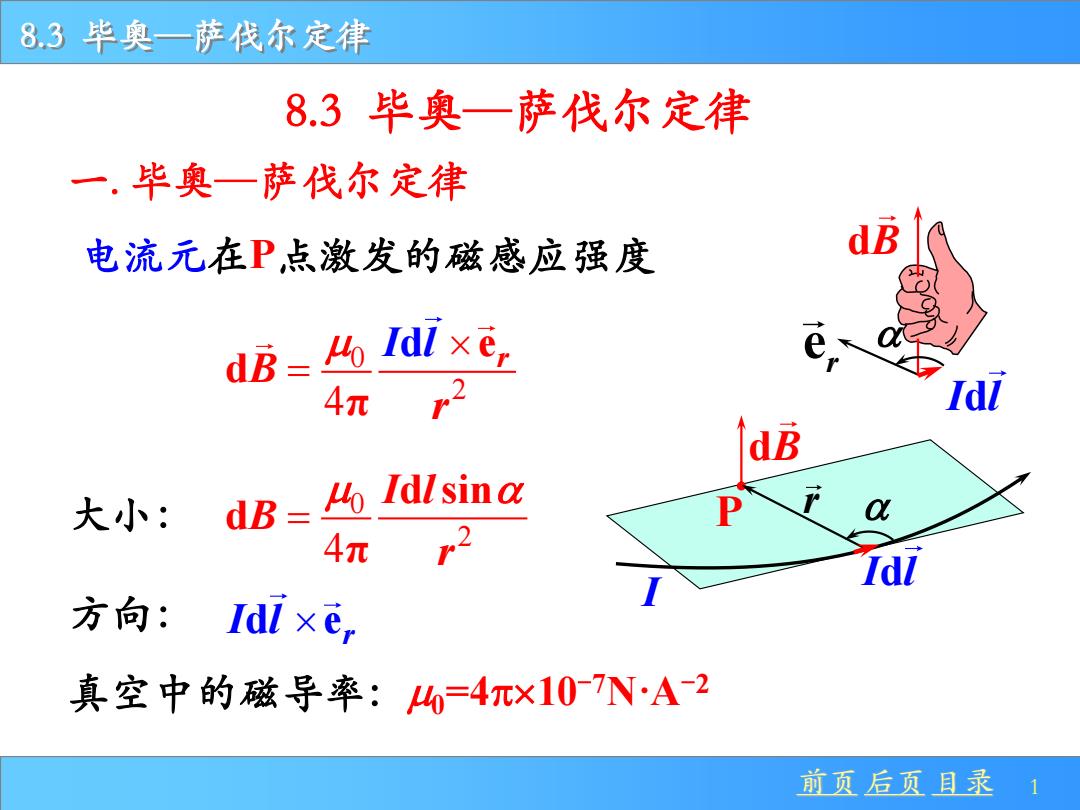
8.3 毕奥—萨伐尔定律 前页 后页 目录 1 一. 毕奥—萨伐尔定律 电流元在P点激发的磁感应强度 dB P r I l d I 大小: 0 2 4 d sin d π I l B r = 方向: d er I l 0 2 4 d e d π r I l Β r = 真空中的磁导率:0=410-7N·A-2 8.3 毕奥—萨伐尔定律 e r I l d dB
83毕奥一萨伐尔定律 B=[dB 线电流在P点激发的磁感应强度 e B=rIdi×e 4π d 前页后页且录2
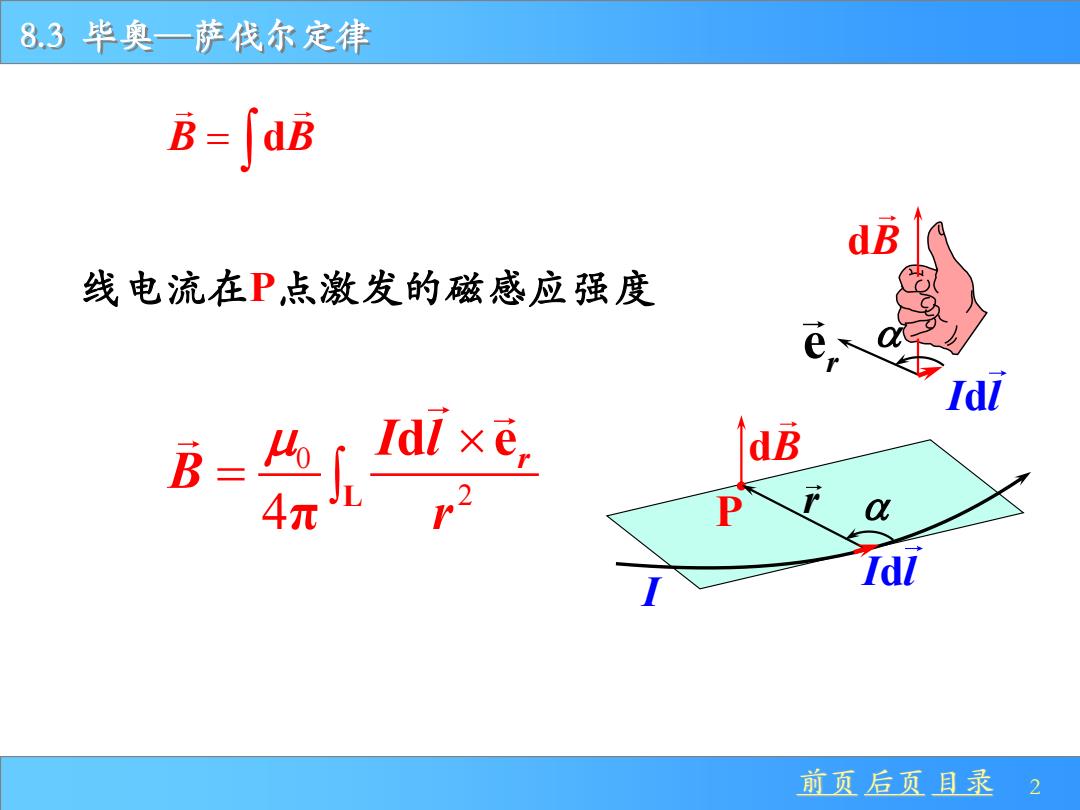
8.3 毕奥—萨伐尔定律 前页 后页 目录 2 0 2 4 L d e π r I l B r = 线电流在P点激发的磁感应强度 Β = dΒ e r I l d dB dB P r I l d I
83毕奥一萨伐尔定律 二.运动电荷的磁场 形成 激发 电流 电荷运动 磁场 激发 电流强度 I=dg=gnSo dt -gnSv dt 电流元与运动电荷的关系 d Idl gnSidl 前页后页目录3
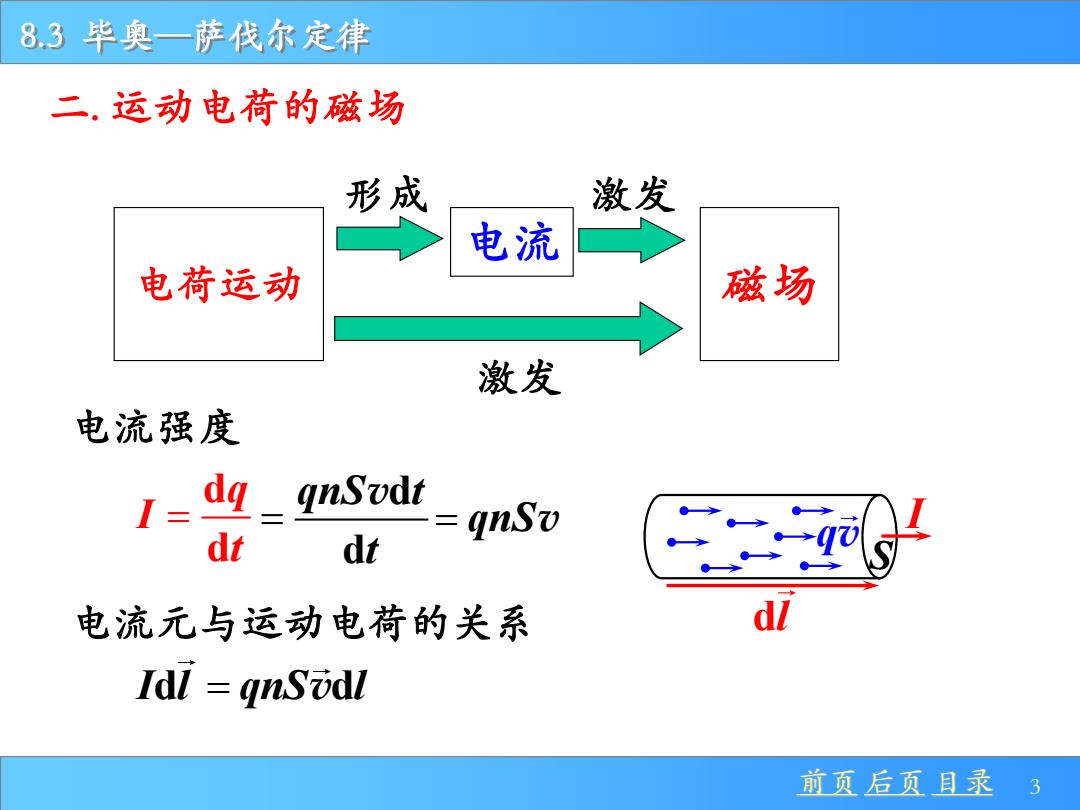
8.3 毕奥—萨伐尔定律 前页 后页 目录 3 电荷运动 形成 电流 激发 磁场 激发 I dl S qv 电流强度 d d q I t = d d qnS t t = v 电流元与运动电荷的关系 I l qnS l d d = v 二. 运动电荷的磁场 = qnSv
8.3毕奥一萨伐尔定律 由电流元的磁感应强度 dB=4oldi×e, 4元 2 电荷q产生的磁感应强度 dB uo Idlxe B,aN4πr 由于Ial=gns dN nSdl =qò 前页后页目录4
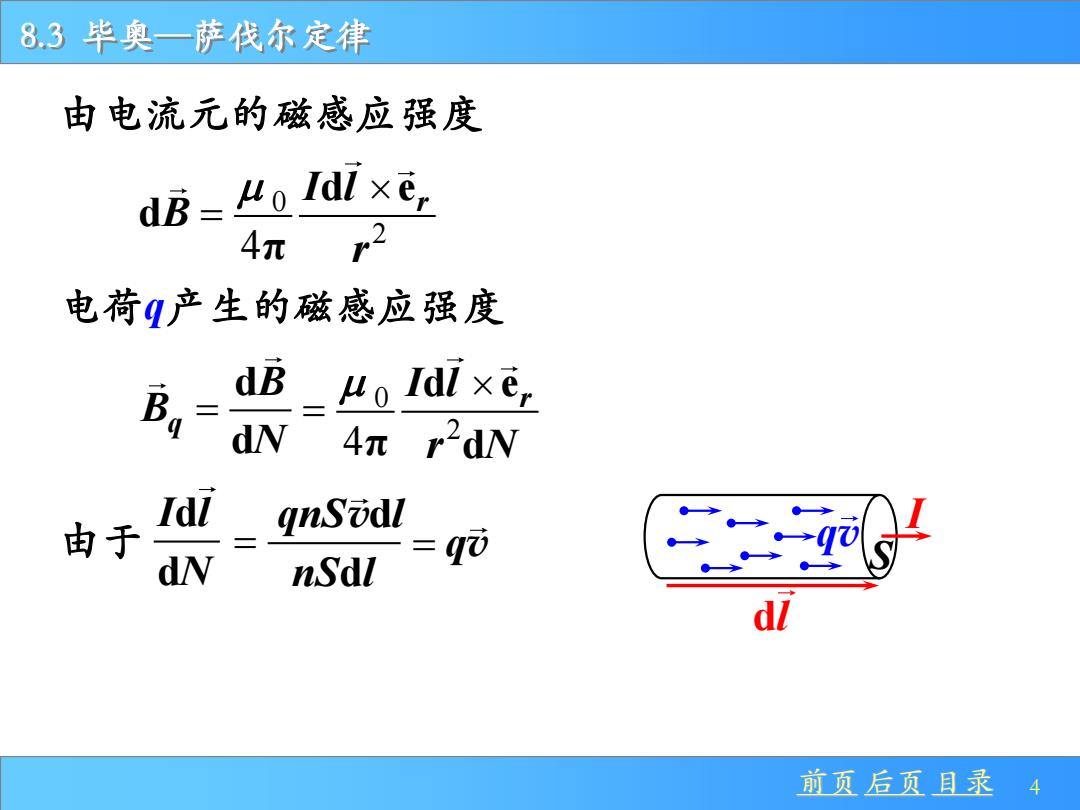
8.3 毕奥—萨伐尔定律 前页 后页 目录 4 由电流元的磁感应强度 电荷q产生的磁感应强度 0 2 4 d e π d r I l r N = 由于 d d I l N I dl S qv 0 2 4 d e d π r I l Β r = d d q Β Β N = nS l d = = qv qnS l vd
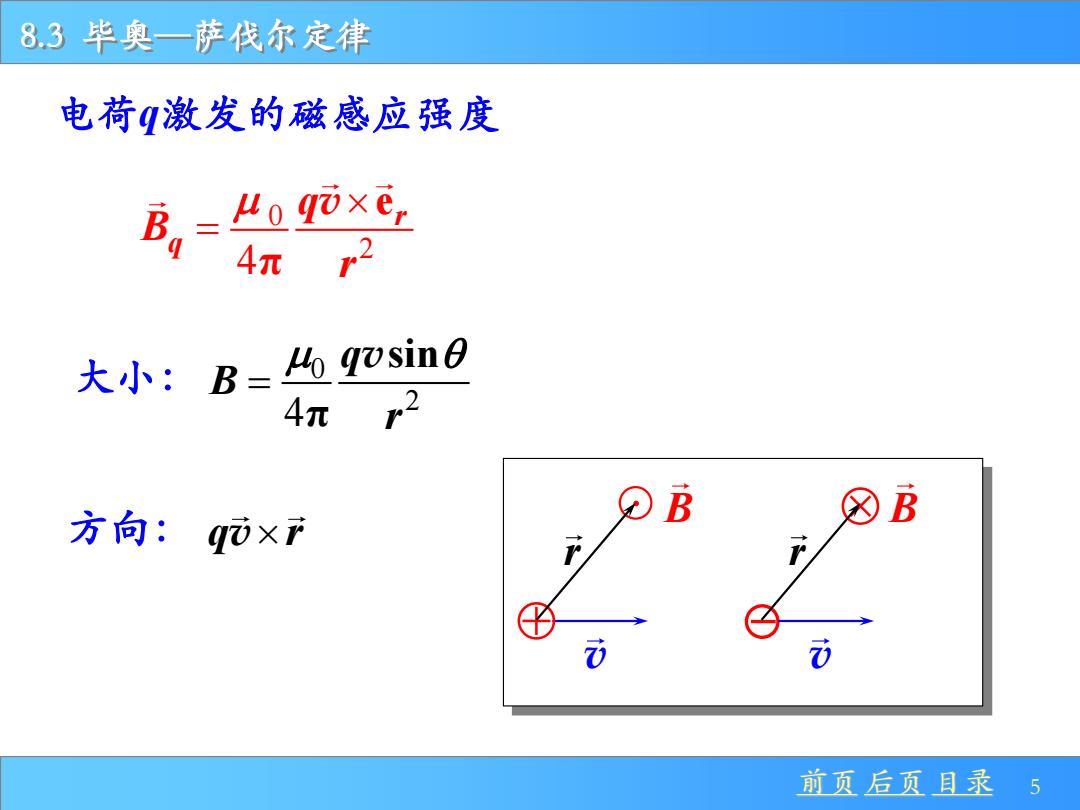
8.3毕奥一萨伐尔定律 电荷激发的磁感应强度 B =Ho qixe, 4πr2 大小:B=也wsin0 4π2 方向:q0×f 刀B ☒B 前页后页且录5
8.3 毕奥—萨伐尔定律 前页 后页 目录 5 电荷q激发的磁感应强度 0 2 4 e π r q q Β r = v 大小: 0 2 4 sin π q B r = v 方向: q r v v B r v B r
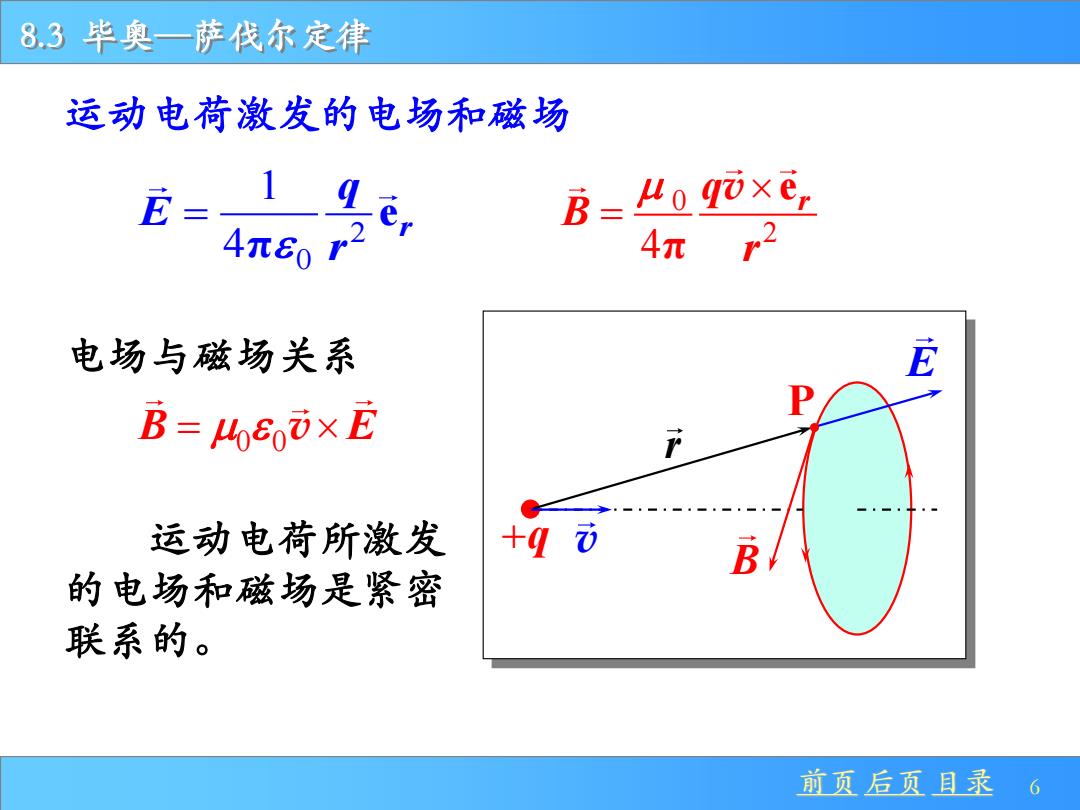
8.3毕奥一萨伐尔定律 运动电荷激发的电场和磁场 E= B=“oqi×e, 4πer2 4πr2 电场与磁场关系 B=he0×E 运动电荷所激发 +ò 的电场和磁场是紧密 联系的。 前页后页目录6
8.3 毕奥—萨伐尔定律 前页 后页 目录 6 运动电荷激发的电场和磁场 2 0 1 4 e π r q E r = 0 2 4 e π r q Β r = v +q v B P r 电场与磁场关系 E B E = 0 0v 运动电荷所激发 的电场和磁场是紧密 联系的

8.3毕奥一萨伐尔定律 三.毕奥一萨伐尔定律的应用 dB=Ho ldixe, 4π r2 B=dB 1.dB方向不变的问题 dB=Ho Idl sina 4n2 前页后页目录 7
8.3 毕奥—萨伐尔定律 前页 后页 目录 7 三. 毕奥—萨伐尔定律的应用 Β = dΒ 0 2 4 d e d π r I l Β r = 1. dΒ 方向不变的问题 0 2 4 d d sin π I l Β r = 0 2 4 d sin π I l Β r =

83毕奥一萨伐尔定律 2.dB方向变的问题 对称性分析,简化问题,再运算。 直角坐标系中 dB=dBxi+dByj+dB,k Bx=∫dBB,=∫dB, B=∫dB B=B i+Byj+B,k 前页后页且录8
8.3 毕奥—萨伐尔定律 前页 后页 目录 8 d d d d Β Βx y z = + + i Β j Β k Βx x = dΒ Βy y = dΒ Βz z = dΒ Β Βx y z = + + i Β j Β k 直角坐标系中 2. dΒ 方向变的问题 对称性分析,简化问题,再运算

8.3毕奥一萨伐尔定律 例1载流长直导线的磁场。P341例题1 解:建立图示坐标系, 电流元在P,点的磁感强度 dB=Holdi xe dy 4π r2 大小:dB=4 Isina 4n2'y 方向:⑧(垂直于板面向里) 垂直于导线。 dB P点磁感强度大小B=dB Px 前页后页目录 9
8.3 毕奥—萨伐尔定律 前页 后页 目录 9 解:建立图示坐标系, 0 2 4 d e d π r I l Β r = 大小: 0 2 4 sin d d π I Β y r = 方向:(垂直于板面向里) 垂直于导线。 o x y a I y dy r 例1 载流长直导线的磁场。 P341例题1 P dB 电流元在P点的磁感强度 P点磁感强度大小 L B B = d

8.3毕奥一萨伐尔定律 B=「Isina JL4元2 dy 由几何关系得 sina cos B dy y=atan B cos B dy = dB cos2B dB P x 积分范围月~B2 前页后页目录10
8.3 毕奥—萨伐尔定律 前页 后页 目录 10 o x y a I y dy r P dB 0 2 L 4 sin d π I B y r = 由几何关系得 sin cos = y a = tan cos a r = 2 d d cos a y = 2 1 积分范围 1 2