7.6静电场中的导体 7.6静电场中的导体 一.导体的静电平衡 静电感应 感应电荷 静电平衡 导体静电平衡必要条件: 导体内部场强处处为零。 E。+E'=0 前页后页目录 1
前页 后页 目录 1 7.6 静电场中的导体 静电感应 感应电荷 静电平衡 导体静电平衡必要条件: 导体内部场强处处为零。 0 E + E 7.6 静电场中的导体 一. 导体的静电平衡 = 0

7.6静电场中的导体 导体静电平衡时 场强: 导体内部场强处处为零。 导体表面附近的场强垂直于表面。 电势: 导体上电势处处相等。(导体是等势体,导 体表面是等势面) 电荷分布: 导体中处处没有净电荷。(电荷只能分布在导 体表面) 前页后页目录2
前页 后页 目录 2 7.6 静电场中的导体 P 导体静电平衡时 场强: 导体内部场强处处为零。 导体表面附近的场强垂直于表面。 电势: 导体上电势处处相等。(导体是等势体,导 体表面是等势面) 电荷分布: 导体中处处没有净电荷。(电荷只能分布在导 体表面) E

7.6静电场中的导体 二.静电平衡时,导体上的电荷分布 1.实心导体 导体内部处处没有净电荷,电 荷只分布在导体表面上。 用高斯定理证明 ∑9 求EaS= 60 龙=0 ∑9=0 S→0 S 前页后页目录 3
前页 后页 目录 3 7.6 静电场中的导体 1.实心导体 + + + + + + + + + + + + + 导体内部处处没有净电荷,电 荷只分布在导体表面上。 S 0 S S d q E S = 内 用高斯定理证明 E = 0 0 S q = 内 二. 静电平衡时,导体上的电荷分布 S → 0
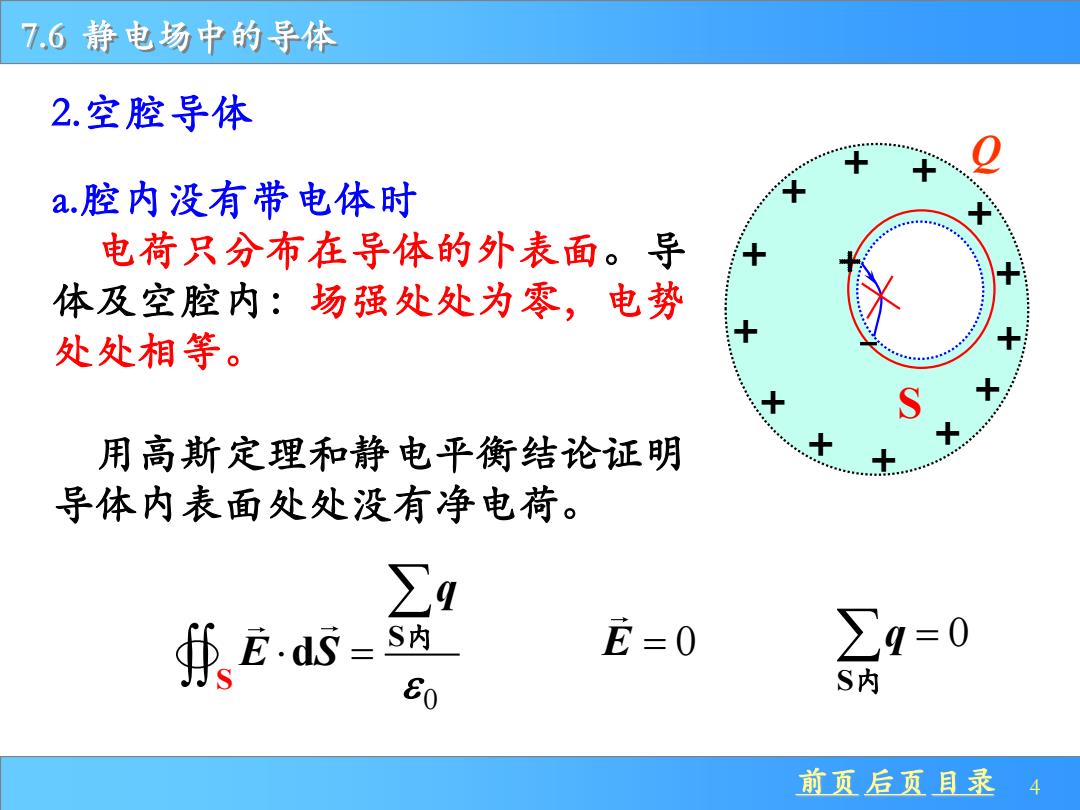
7.6静电场中的导体 2.空腔导体 a.腔内没有带电体时 电荷只分布在导体的外表面。导 体及空腔内:场强处处为零,电势 处处相等。 用高斯定理和静电平衡结论证明 导体内表面处处没有净电荷。 ∑4 承Eds S E=0 ∑9=0 E0 S内 前页后页目录 4
前页 后页 目录 4 7.6 静电场中的导体 2.空腔导体 + + + + + + + + + + + + + Q 0 S S d q E S = 内 a.腔内没有带电体时 电荷只分布在导体的外表面。导 体及空腔内:场强处处为零,电势 处处相等。 S 用高斯定理和静电平衡结论证明 导体内表面处处没有净电荷。 E = 0 0 S q = 内
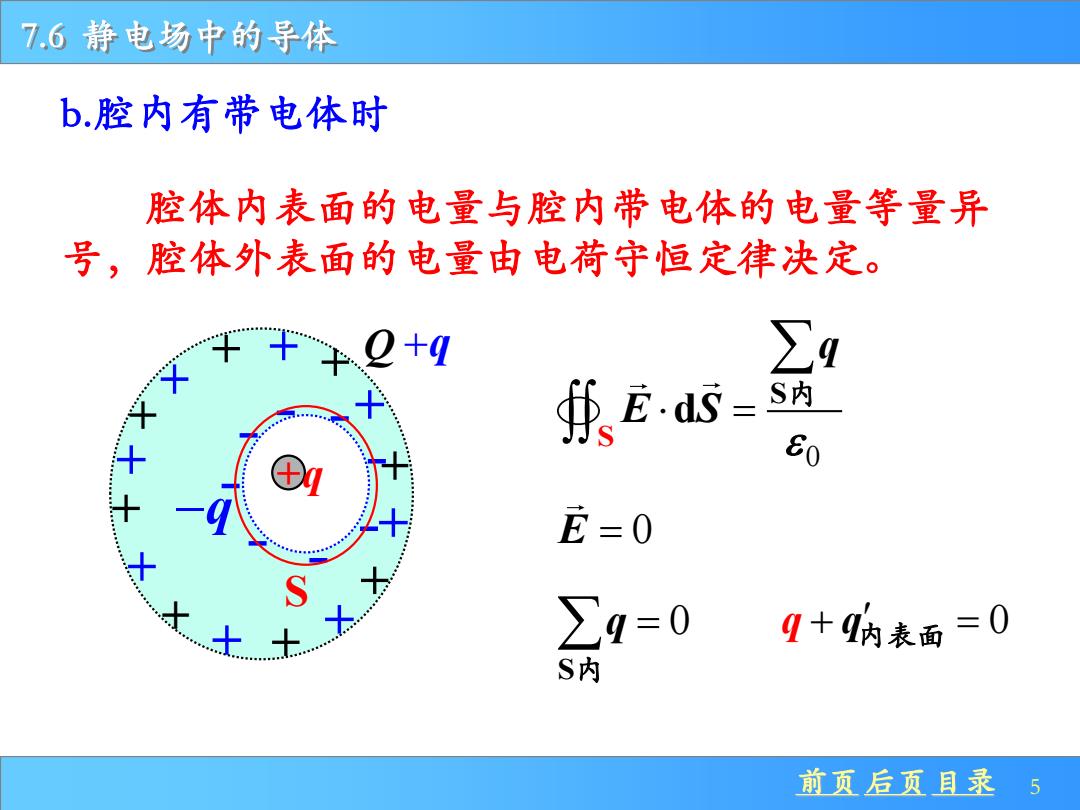
7.6静电场中的导体 b.腔内有带电体时 腔体内表面的电量与腔内带电体的电量等量异 号,腔体外表面的电量由电荷守恒定律决定。 ∑9 求Ea5= 80 龙=0 S ∑9=0 9+纳表面=0 S 前页后页目录 5
前页 后页 目录 5 7.6 静电场中的导体 b.腔内有带电体时 +q + + + + + Q + + + +q + + + + + + + + −q 0 S S d q E S = 内 S E = 0 0 S q = 内 q + = q内 表面 0 腔体内表面的电量与腔内带电体的电量等量异 号,腔体外表面的电量由电荷守恒定律决定
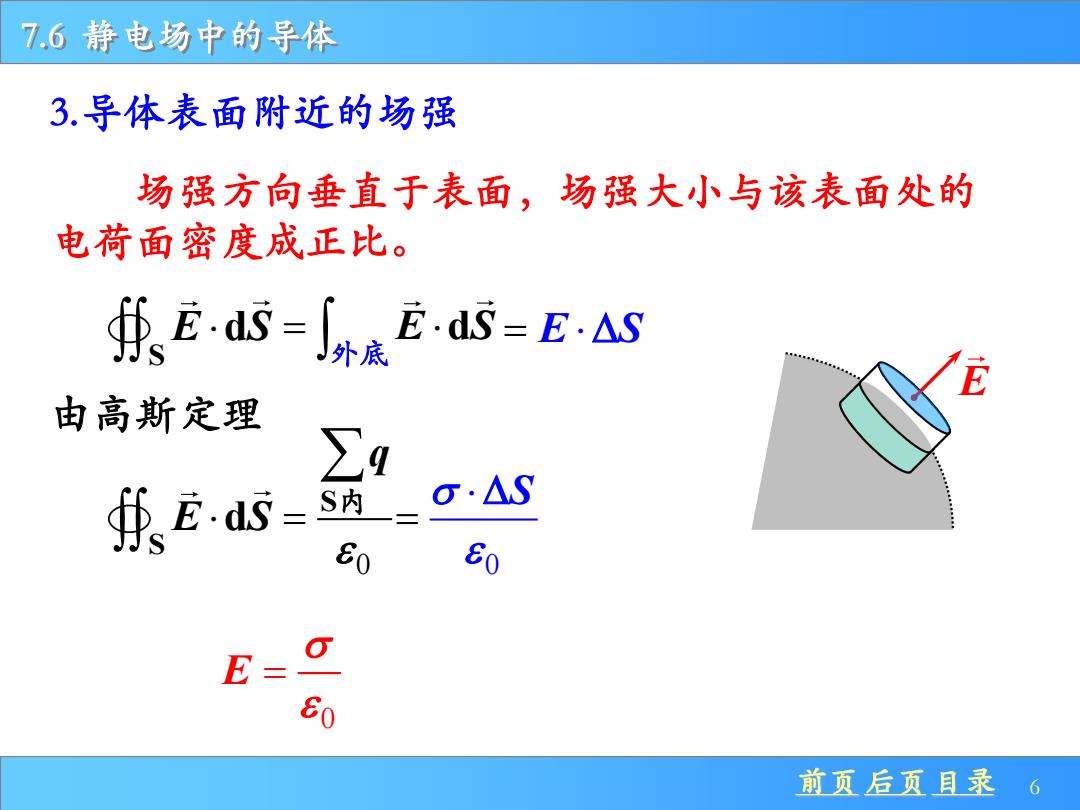
7.6静电场中的导体 3.导体表面附近的场强 场强方向垂直于表面,场强大小与该表面处的 电荷面密度成正比。 乐Ed=j外度EdS=EAS 由高斯定理 正4 求Ed5=药_g·AS 80 60 E= 0 的 前页后页目录6
前页 后页 目录 6 7.6 静电场中的导体 3.导体表面附近的场强 E S E S d = E Sd 外底 = E S 由高斯定理 0 S S d q E S = 内 0 S = 0 E = 场强方向垂直于表面,场强大小与该表面处的 电荷面密度成正比

7.6静电场中的导体 4.孤立导体表面电荷分布 表面曲率越大,面电荷密度越大。 尖端放电现象 前页后页目录 7
前页 后页 目录 7 7.6 静电场中的导体 4.孤立导体表面电荷分布 表面曲率越大,面电荷密度越大。 尖端放电现象

7.6静电场中的导体 例1半径分别为R和r的两个球形导体(R>)相距 很远,用一根很长的细导线连接起来,让导体球带电。 求:球面上电荷面密度与半径的关系。P287 解:忽略细导线电量 12_1_4 4n60R4π60r 4π 2=R OR=- gr 4nR2 0r=2.2 OR_r o,9R2 O R 本题完 前页后页目录8
前页 后页 目录 8 7.6 静电场中的导体 例1 半径分别为R和r的两个球形导体(R>r)相距 很远,用一根很长的细导线连接起来,让导体球带电。 求:球面上电荷面密度与半径的关系。P287 Q q 解:忽略细导线电量 0 0 1 1 4 4 π π Q q R r = Q R q r = 2 4π R Q R = 2 4π r q r = 2 2 R r Q r q R = R r r R = 本题完
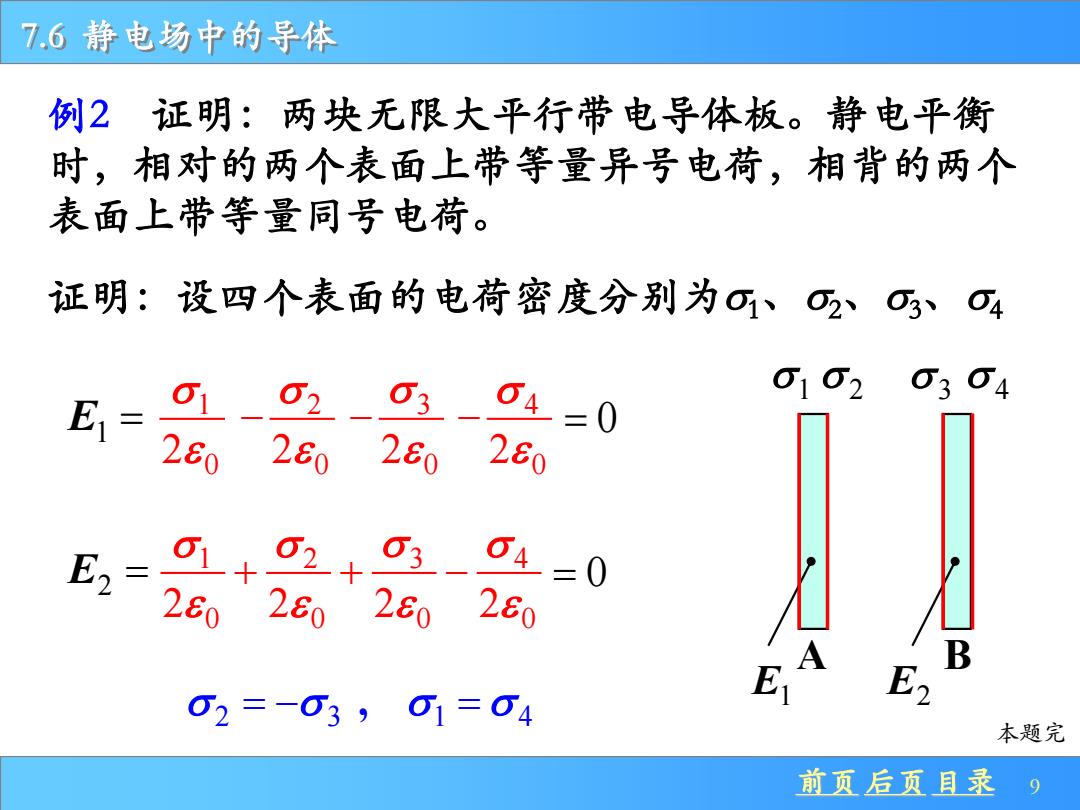
7.6静电场中的导体 例2证明:两块无限大平行带电导体板。静电平衡 时,相对的两个表面上带等量异号电荷,相背的两个 表面上带等量同号电荷。 证明:设四个表面的电荷密度分别为O、O2、O3O4 1-02-03-04=0 01020304 E= 260260260 280 E2= 1+02+03-04=0 2e26026280 E 02=-03,01=04 本题完 前页后页目录 9
前页 后页 目录 9 7.6 静电场中的导体 例2 证明:两块无限大平行带电导体板。静电平衡 时,相对的两个表面上带等量异号电荷,相背的两个 表面上带等量同号电荷。 证明:设四个表面的电荷密度分别为1、2、3、4 1 2 3 4 E1 = E2 = 2 3 1 4 = − = , 本题完 E1 E2 A B 1 0 2 2 0 2 − 3 0 2 − 4 0 2 − = 0 1 2 4 3 0 0 0 0 2 2 2 2 ++− = 0
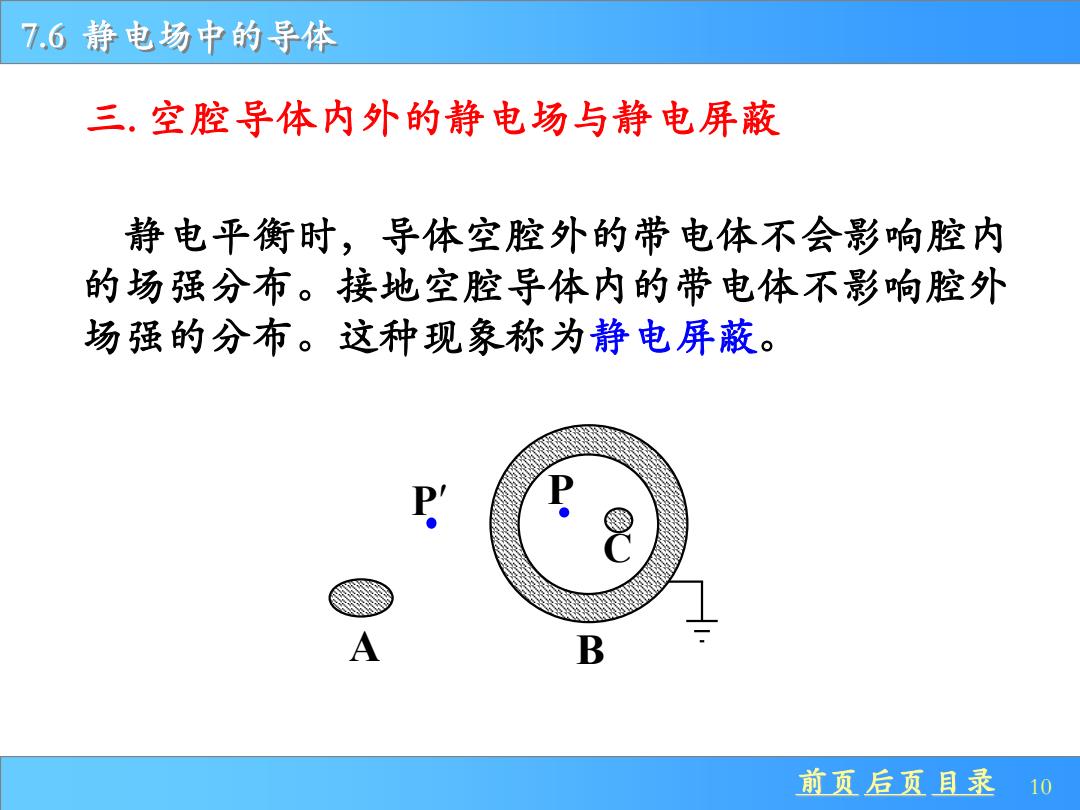
7.6静电场中的导体 三.空腔导体内外的静电场与静电屏蔽 静电平衡时,导体空腔外的带电体不会影响腔内 的场强分布。接地空腔导体内的带电体不影响腔外 场强的分布。这种现象称为静电屏蔽。 前页后页目录 10
前页 后页 目录 10 7.6 静电场中的导体 静电平衡时,导体空腔外的带电体不会影响腔内 的场强分布。接地空腔导体内的带电体不影响腔外 场强的分布。这种现象称为静电屏蔽。 三. 空腔导体内外的静电场与静电屏蔽 A B C P P