
7.10静电场的能量 7.10静电场的能量 电容为C的电容器,带电量为 q。将正点电荷dq从负极板移到正 极板外力作的功 + dA-Udg-dg 电容器充电,电量从0到 ⊕ 2,外力作的功 A= 2且dq= 2 Jo C 2C 前页后页目录 1
前页 后页 目录 1 7.10 静电场的能量 7.10 静电场的能量 dq 电容为C的电容器,带电量为 q。将正点电荷dq从负极板移到正 极板外力作的功 d d A U q = d q q C = 电容器充电,电量从0到 Q,外力作的功 0 d Q q A q C = 2 2 Q C = +q −q C

7.10静电场的能量 电容器的静电能 平行板电容器C=6 W= o. d -x 2C 280S + -0 将电源断开(Q不变)。把负极 板从x移到x+dr处,静电能的增量 dW=. -dx 280S 能量密度w。= dw 02 Sdx 280S2 前页后页且录2
前页 后页 目录 2 7.10 静电场的能量 2 2 Q W C = 电容器的静电能 +Q −Q x dx 将电源断开(Q不变)。把负极 板从x移到x+dx处,静电能的增量 2 0 2 Q x S = 2 0 2 d d Q W x S = 能量密度 e d d W w S x = 平行板电容器 2 o x 2 0 2 Q S = 0S C d =
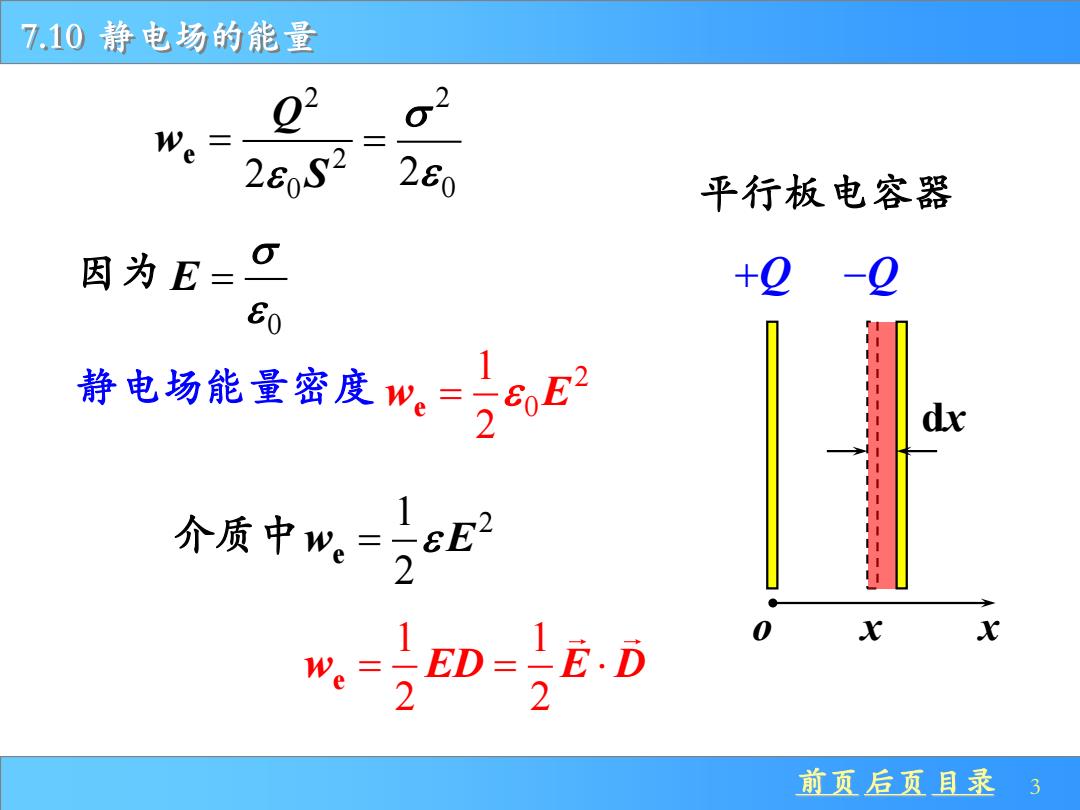
7.10静电场的能量 02 02 We= 260S2 280 平行板电容器 因为E=口 +0-0 80 静电场能量密度w。=,6E2 介质中w。=三εE2 =ED=ED 2 2 前页后页目录 3
前页 后页 目录 3 7.10 静电场的能量 +Q −Q x dx 平行板电容器 o x 2 2 0 2 e Q w S = 2 0 2 = 0 E = 2 0 1 2 w E e = 因为 静电场能量密度 介质中 1 2 2 w E e = 1 1 2 2 w ED E D e = =
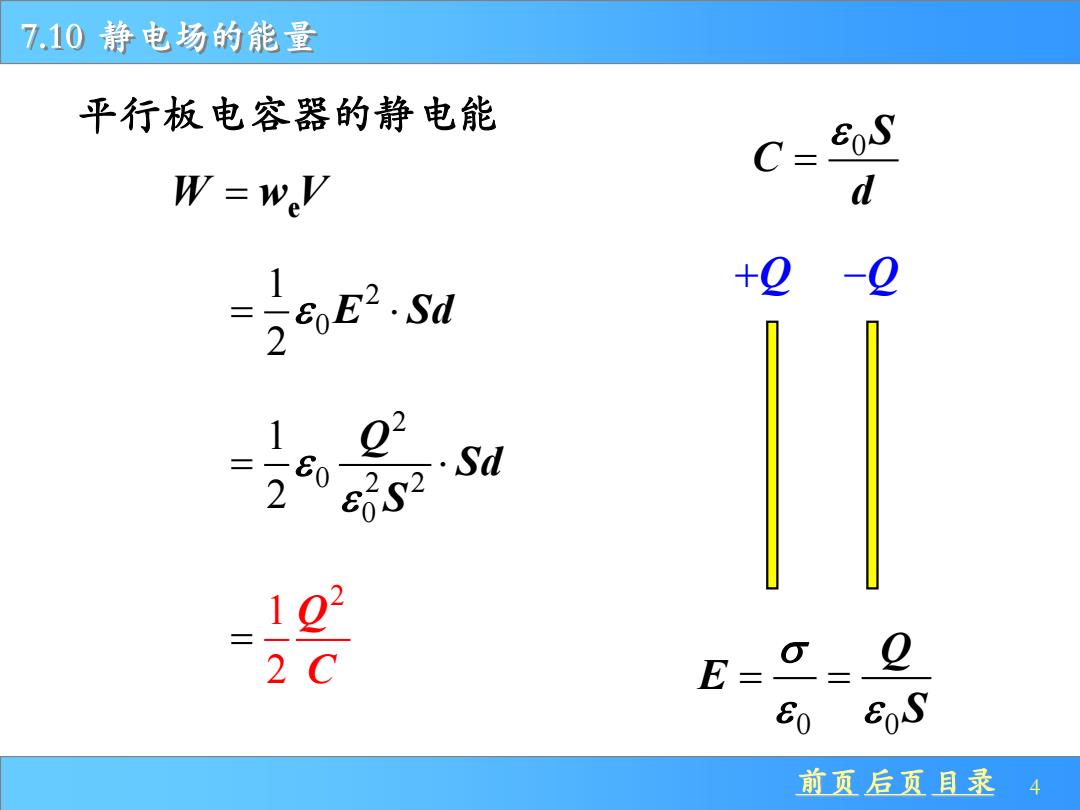
7.10静电场的能量 平行板电容器的静电能 C= W=wV d 2602.Sd 1 +Q-0 _02 580 2 Sd 102 2C E== E0 8oS 前页后页目录 4
前页 后页 目录 4 7.10 静电场的能量 +Q −Q 平行板电容器的静电能 0S C d = W w V = e 2 0 1 2 = E Sd 0 0 Q E S = = 2 0 2 2 0 1 2 Q Sd S = 2 1 2 Q C =

7.10静电场的能量 静电场能量 静电场离不开带电体。交变电磁场可以脱 离带电体独立存在,证明电磁场的能量储存在 场中。 能量是物质的固有属性之一,静电场具有 能量的结论,证明静电场是一种特殊形态的物 质。 前页后页目录 5
前页 后页 目录 5 7.10 静电场的能量 静电场能量 e V W w V = d 静电场离不开带电体。交变电磁场可以脱 离带电体独立存在,证明电磁场的能量储存在 场中。 能量是物质的固有属性之一,静电场具有 能量的结论,证明静电场是一种特殊形态的物 质
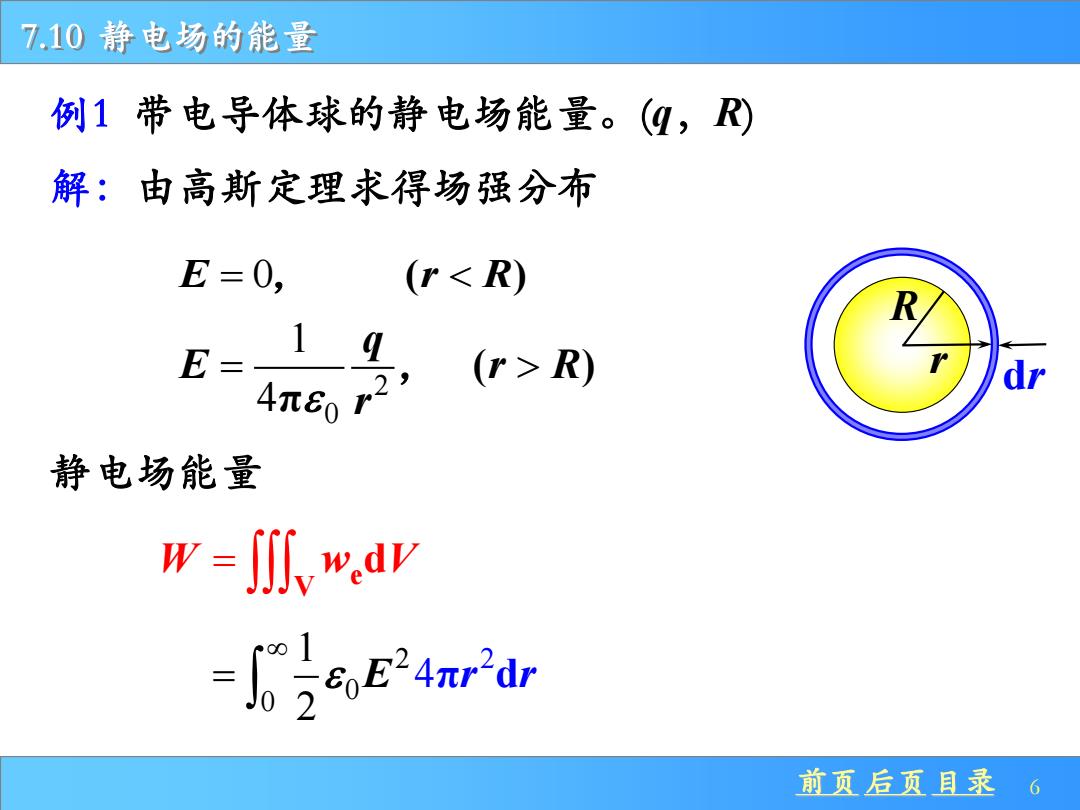
7.10静电场的能量 例1带电导体球的静电场能量。(q,) 解:由高斯定理求得场强分布 E=0, (rR) 静电场能量 W=八w,d业 ridr 前页后页目录、6
前页 后页 目录 6 7.10 静电场的能量 R 例1 带电导体球的静电场能量。(q,R) 解:由高斯定理求得场强分布 E r R = 0, ( ) 2 0 1 4 ( ) π q E r R r = , 静电场能量 e V W w V = d 0 2 2 0 4 1 2 E πr r d = r dr
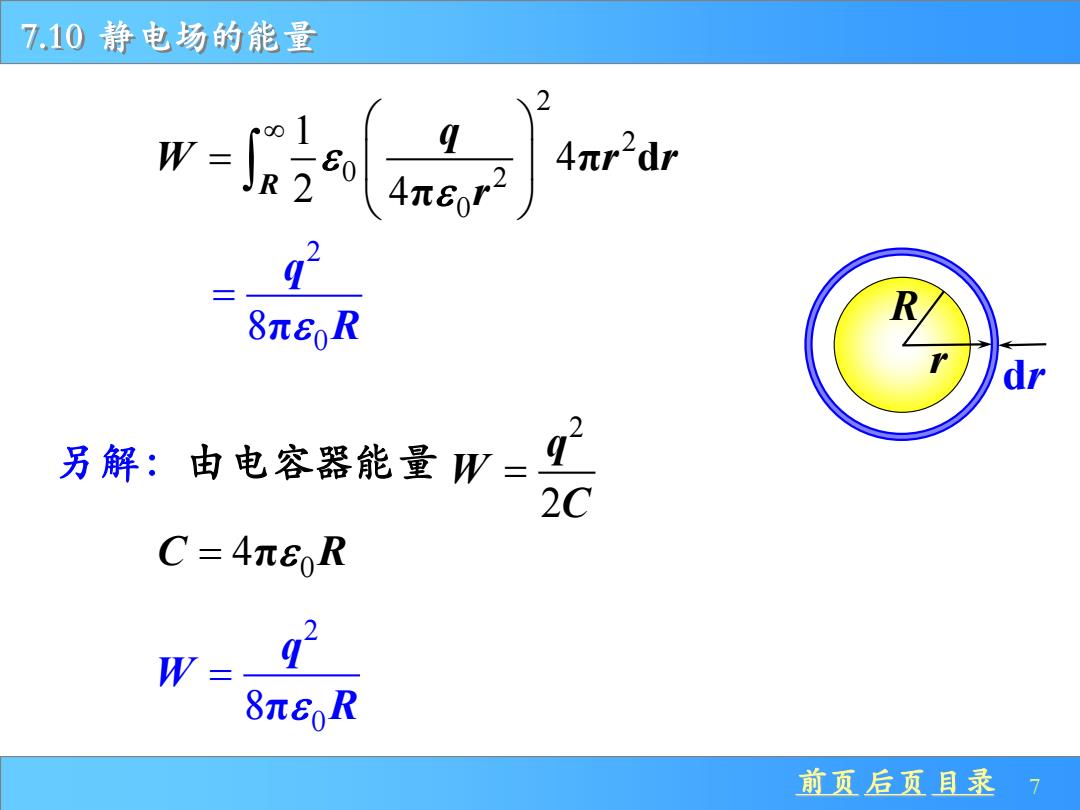
7.10静电场的能量 2 00 4πr2dr 4π80r1 92 R 8πEoR 另解:由电容器能量W= C=4π60R 8π6oR 前页后页目录 7
前页 后页 目录 7 7.10 静电场的能量 2 2 0 2 0 1 4 2 4 π d π R q W r r r = 2 0 8π q R = 另解:由电容器能量 2 2 q W C = 0 C R = 4π 2 0 8π q W R = R r dr

7.10静电场的能量 例2空气平行板电容器带电量为2,极板面积为S, 间距为山,断开电源后把极板间距拉大x。求:(I)外 力克服极板相互吸引力所作的功;(②)极板间的相互 吸引力。 +0-0 解:(1)间距改变d山x外力作的功 dx d4=dW = dx 260S 间距增加x外力作的功 +x22 A=d 02 dx= 28S 前页后页且录8
前页 后页 目录 8 7.10 静电场的能量 例2 空气平行板电容器带电量为Q,极板面积为S, 间距为d,断开电源后把极板间距拉大x。求:(1)外 力克服极板相互吸引力所作的功;(2)极板间的相互 吸引力。 解:(1) 间距改变dx外力作的功 2 0 2 d d d Q A W x S = = 间距增加x外力作的功 2 0 2 d d x d Q A x S + = 2 0 2 Q x S = x dx o x +Q −Q

7.10静电场的能量 (2)间距改变dx外力作的功 d4=Fdx 比较前式得F= 92 +0 -0 280S 极板间的相互吸引力与 外力等值反向。 另解:用电场力的叠加求解 dF Edg E=e=Eg=28上Q9 280S 本节完 前页后页目录 .9
前页 后页 目录 9 7.10 静电场的能量 (2)间距改变dx外力作的功 d d A F x = 比较前式得 2 0 2 Q F S = 极板间的相互吸引力与 外力等值反向。 +Q −Q 另解:用电场力的叠加求解 = E qd F = E qd 0 2 ( ) Q = − 2 0 2 Q S − = dq E dF = E qd 本节完