5.2分子热运动和统计规律 5.2分子热运动和统计规律 一.分子热运动图像 布 运 动 分子热运动:大量分子做永不停息的无规则运动。 前页后页目录 1
前页 后页 目录 1 5.2 分子热运动和统计规律 一. 分子热运动图像 分子热运动:大量分子做永不停息的无规则运动。 布 朗 运 动 5.2 分子热运动和统计规律

5.2分子热运动和统计规律 气体分子热运动的基本量: 1)分子数密度3×1019cm3; 2)分子间距约为分子线度的10倍; 3)碰撞以外,分子间作用力极小; 4)分子热运动的平均速度500m/s; 5)分子热运动的平均自由程10-7m; 6分子热运动的平均碰撞次数1010s1。 前页后页目录 2
前页 后页 目录 2 5.2 分子热运动和统计规律 气体分子热运动的基本量: 1)分子数密度31019/cm3 ; 2)分子间距约为分子线度的10倍; 3)碰撞以外,分子间作用力极小; 4)分子热运动的平均速度500m/s ; 5)分子热运动的平均自由程10-7m; 6)分子热运动的平均碰撞次数1010s -1

5.2分子热运动和统计规律 二.分子热运动的基本特征 分子的永恒运动与频繁的相互碰撞。 1)无序性(混乱性) 2)统计性(规律性) 3)微观量每个分子的特征量。 4)宏观量大量分子整体的特征量。 5)起伏现象 前页后页目录3
前页 后页 目录 3 5.2 分子热运动和统计规律 二. 分子热运动的基本特征 分子的永恒运动与频繁的相互碰撞。 1) 无序性(混乱性) 2) 统计性(规律性) 3) 微观量 每个分子的特征量。 4) 宏观量 大量分子整体的特征量。 5) 起伏现象

5.2分子热运动和统计规律 三.分布函数和平均值 偶然事件:不可预测的而又大量出现的事件 实例:2009江苏高考分数段成绩统计 分布数△N 分数段x~x+x的人数 归一化分布数fy)=心 N N=∑AWx 归一化】 W=∑袋1 前页后页目录 4
前页 后页 目录 4 5.2 分子热运动和统计规律 三. 分布函数和平均值 偶然事件:不可预测的而又大量出现的事件 = ΔNx N 归一化 实例:2009江苏高考分数段成绩统计 分布数 ΔNx 归一化分布数 = Δ ( ) Nx f x N N N = Δ x 分数段 x x x + Δ 的人数 f x( ) =1
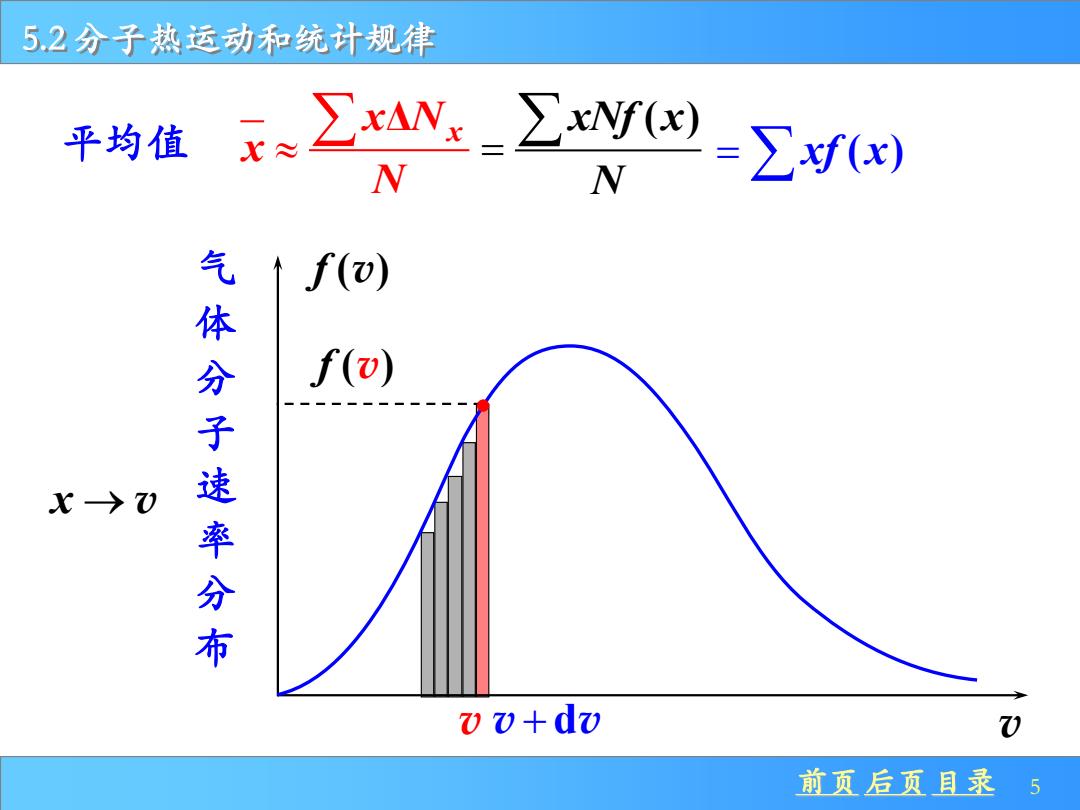
5.2分子热运动和统计规律 平均值 ∑xaNs_∑Wrw N N =∑f(x 气 ↑f(w) 体 分 f() 子 分 布 00+do 前页后页目录 5
前页 后页 目录 5 5.2 分子热运动和统计规律 平均值 Δ x x N x N = xNf x( ) N = xf x( ) f ( ) v v f ( ) v v v v + d 气 体 分 子 速 率 分 布 x → v

5.2分子热运动和统计规律 气体速率分布函数 f(o)= dN Ndo N=∫dW=∫Nf(odo 归一化条件 f(o)do=1 平均速率 odN Nf(o)do 0= N N =」of(w)dw 本节完 前页后页目录 6
前页 后页 目录 6 5.2 分子热运动和统计规律 气体速率分布函数 = d ( ) d N f N v v = N Nd 归一化条件 =1 f ( )d v v= Nf ( )d v v 平均速率 = dN N v v Nf ( )d N = v v v = v v v f ( )d 本节完