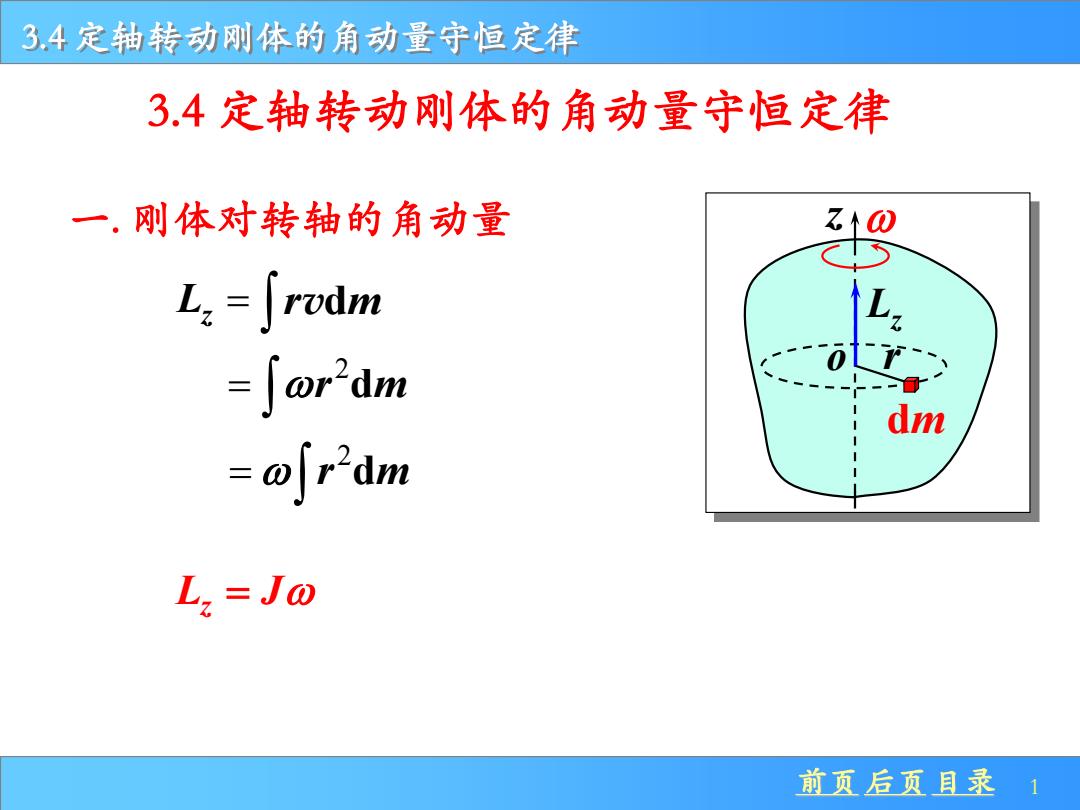
3,4定轴转动刚体的角动量守恒定律 3.4定轴转动刚体的角动量守恒定律 一.刚体对转轴的角动量 Z个0 L:=∫rzdm L. =∫or2dm dm =@fr2dm L=Jo 前页后页目录1
前页 后页 目录 1 3.4 定轴转动刚体的角动量守恒定律 一. 刚体对转轴的角动量 2 = r md o r dm z Lz 3.4 定轴转动刚体的角动量守恒定律 Lz = r m vd 2 = r md L J z =

3.4定轴转动刚体的角动量守恒定律 二.定轴转动刚体的角动量定理 由定轴转动定律 M.-Jad)d(L 分离变量,两边积分得 %M.d=4。-L0 1.力对转轴的冲量矩 [M.dt 前页后页目录2
前页 后页 目录 2 3.4 定轴转动刚体的角动量守恒定律 二. 定轴转动刚体的角动量定理 由定轴转动定律 M J z = 分离变量,两边积分得 0 0 d t z z z t M t L L = − d ( ) d J t = 1.力对转轴的冲量矩 0 d t z t M t d ( ) d Lz t =

3.4定轴转动刚体的角动量守恒定律 2.角动量定理 定轴转动中,外力对转轴的冲量矩等于刚体对 该轴的角动量增量。 M.de -1-Lo 微分形式M2= dl: dt 前页后页目录3
前页 后页 目录 3 3.4 定轴转动刚体的角动量守恒定律 2.角动量定理 d d z z L M t 微分形式 = 定轴转动中,外力对转轴的冲量矩等于刚体对 该轴的角动量增量。 0 0 d t z z z t M t L L = −

3,4定轴转动刚体的角动量守恒定律 三.定轴转动刚体的角动量守恒定律 角动量守恒定律 外力对定轴的合力矩为零时,系统对该轴的角 动量L,将保持不变。 条件合力矩为零M,=0 结论L,=恒量 或J0=恒量 角动量守恒的两种情况: (1)J保持不变时,则其角速度恒定,即匀速转动 J=恒量 ⑩=恒量 前页后页目录4
前页 后页 目录 4 3.4 定轴转动刚体的角动量守恒定律 三. 定轴转动刚体的角动量守恒定律 条件 合力矩为零 Mz=0 结论 Lz =恒量 角动量守恒定律 外力对定轴的合力矩为零时,系统对该轴的角 动量Lz将保持不变。 角动量守恒的两种情况: (1)J保持不变时,则其角速度恒定,即匀速转动 J=恒量 =恒量 或 J =恒量

3.4定轴转动刚体的角动量守恒定律 (②)对刚体组(或质点组),J变化时,其角速度也会 变化,但它们的积不变。 L,=J0=J0=恒量 角动量守恒视频演示 前页后页目录5
前页 后页 目录 5 3.4 定轴转动刚体的角动量守恒定律 (2)对刚体组(或质点组),J变化时,其角速度也会 变化,但它们的积不变。 L J J z = = = 0 0 恒量 角动量守恒视频演示

3,4定轴转动刚体的角动量守恒定律 应用 冰上运动 跳水运动 “狂风”直升机 “海王”反潜直升机 前页后页目录6
前页 后页 目录 6 3.4 定轴转动刚体的角动量守恒定律 应用 冰上运动 跳水运动 “狂风”直升机 “海王”反潜直升机

3.4定轴转动刚体的角动量守恒定律 质点直线运动(刚体平动)与定轴转动规律对照 质点直线运动 刚体定轴转动 dx do d2x de d20 0二 d= 0= dr2 dt a= dt dt dt dr2 1 E 2 1 p=mo =-2 2 L=J@ 2 F m M J d4=Fdx Fdt dA=M,d0 M.dt F=ma M,=Ja ∫Fdt=p-Po ∫Mdt=L-Lo m21 2 m00 2 jMd0-之a2-a 前页后页目录7
前页 后页 目录 7 3.4 定轴转动刚体的角动量守恒定律 质点直线运动(刚体平动)与定轴转动规律对照 质点直线运动 刚体定轴转动 d d x t v = d dt = 2 2 d d d d x a t t = = v 2 2 d d dt dt = = p m= v L J z = 1 2 2 E m k = v 1 2 2 E J k = F m M J d d A F x = d d A Mz F t d = M t zd F ma = M J z = F t p p d = − 0 M t L L z z z d = − 0 2 2 0 1 1 2 2 F x m m d = − v v 2 2 0 1 1 2 2 M J J zd = −

3,4定轴转动刚体的角动量守恒定律 例1匀质细棒长为l,质量为m,可绕通过其端点0的 水平轴自由转动,如图所示。当棒从水平位置自由释 放后,在竖直位置上与放在地面上的物体相碰撞。物 体的质量也为m,与地面的摩擦系数为4。相撞后物 体沿地面滑行距离S后停止。求相撞后棒的质心C上升 的最大高度,并说明棒在碰撞后将向左摆或向右摆 的条件。P128例题7 解:第一阶段:棒自由下摆。 以棒和地球为系统,只有重 力作功,机械能守恒。以0,点为重 力势能的零,点。用0表示棒在竖 直位置的角速度,则 前页后页且录8
前页 后页 目录 8 3.4 定轴转动刚体的角动量守恒定律 例1 匀质细棒长为l,质量为m,可绕通过其端点o的 水平轴自由转动,如图所示。当棒从水平位置自由释 放后,在竖直位置上与放在地面上的物体相碰撞。物 体的质量也为m,与地面的摩擦系数为。相撞后物 体沿地面滑行距离s后停止。求相撞后棒的质心c上升 的最大高度h,并说明棒在碰撞后将向左摆或向右摆 的条件。P128例题7 o c 解:第一阶段:棒自由下摆。 以棒和地球为系统,只有重 力作功,机械能守恒。以o点为重 力势能的零点。用表示棒在竖 直位置的角速度,则
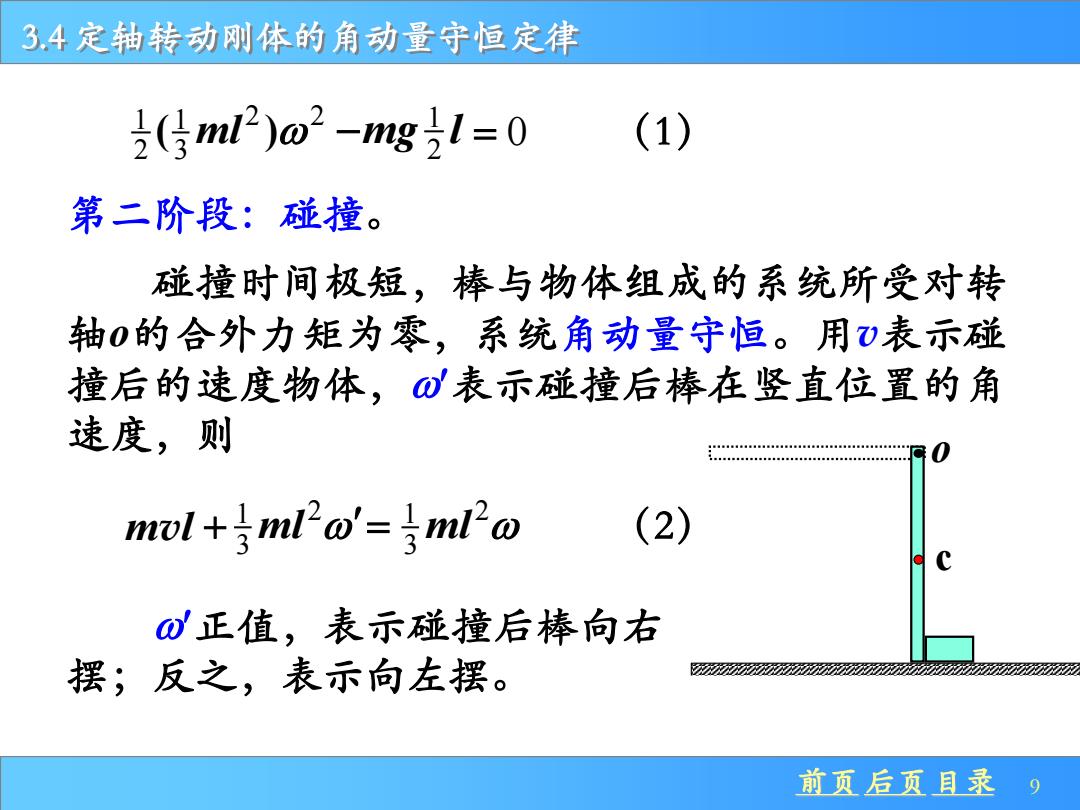
3,4定轴转动刚体的角动量守恒定律 2(gml2)o2-g号1=0 (1) 第二阶段:碰撞。 碰撞时间极短,棒与物体组成的系统所受对转 轴0的合外力矩为零,系统角动量守恒。用)表示碰 撞后的速度物体,⑩表示碰撞后棒在竖直位置的角 速度,则 444444 ml+号ml2o'=3ml2w (2) ⑩正值,表示碰撞后棒向右 摆;反之,表示向左摆。 前页后页且录9
前页 后页 目录 9 3.4 定轴转动刚体的角动量守恒定律 碰撞时间极短,棒与物体组成的系统所受对转 轴o的合外力矩为零,系统角动量守恒。用v表示碰 撞后的速度物体,表示碰撞后棒在竖直位置的角 速度,则 (1) o c 1 1 2 2 2 3( ) ml 第二阶段:碰撞。 m l v (2) 正值,表示碰撞后棒向右 摆;反之,表示向左摆。 1 mg l 2 − = 0 1 2 + 3 ml 1 2 = 3 ml

3,4定轴转动刚体的角动量守恒定律 第三阶段:物体滑行,棒上摆。由物体用动能定理 -umgs =0-mo2 (3) 由以上三式,解得 @13gl-32ugs (4) 当I>6S时,0>0,棒向右摆。 棒上摆用机械能守恒。 前页后页且录 10
前页 后页 目录 10 3.4 定轴转动刚体的角动量守恒定律 第三阶段:物体滑行,棒上摆。由物体用动能定理 (3) 由以上三式,解得 (4) 当l >6s时,'>0,棒向右摆。 −mgs3 3 2 gl gs l − = o c 棒上摆用机械能守恒。 1 2 2 = −0 mv