
25质点系的功能原理机械能守恒定律 2.5质点系的功能原理机械能守恒定律 一.质点系的动能定理 A外+A保内十A非保内=Ek2-Ek1 A保内=-(Ep2-Ep1) A外+A非保内=Ek2-Ek1+Ep2-ED 机械能E=Ek+Ep A外+A非保内=E2-E 前页后页且录1
前页 后页 目录 1 2.5 质点系的功能原理 机械能守恒定律 一. 质点系的动能定理 p p 2 1 A E E 保内 = − − ( ) A A E E E E 外 + = − + − 非保内 k k p p 2 1 2 1 机械能 E E E = + k p 2.5 质点系的功能原理 机械能守恒定律 A A A E E 外 + + = − 保内 非保内 k k 2 1 A A E E 外 + = − 非保内 2 1

2,5质点系的功能原理机械能守恒定律 二,质点系的功能原理 系统外力和非保守内力作功之总和等于机械 能的增量 A外+A非保内=E2-E1 讨论: 1)对质点系动能定理,等式左边是所有外力和 内力作功的总和,等式右边是总动能增量。 2)对质点系功能原理,等式左边是所有外力和 非保守内力作功的总和,等式右边是总机械能增量。 前页后页目录2
前页 后页 目录 2 2.5 质点系的功能原理 机械能守恒定律 A A E E 外 + = − 非保内 2 1 二. 质点系的功能原理 讨论: 1)对质点系动能定理,等式左边是所有外力和 内力作功的总和,等式右边是总动能增量。 2)对质点系功能原理,等式左边是所有外力和 非保守内力作功的总和,等式右边是总机械能增量。 系统外力和非保守内力作功之总和等于机械 能的增量

2,5质点系的功能原理机械能守恒定律 三.机械能守恒定律 如果系统内只有保守力作功,则系统的机械能 就保持不变。 E=Ek+E。=常量 条件A外十A非保内=0 结论dE=0 dEk dEp 0 dEk --dEp 四.能量守恒定律 前页后页且录3
前页 后页 目录 3 2.5 质点系的功能原理 机械能守恒定律 条件 A A 外 + = 非保内 0 结论 dE = 0 如果系统内只有保守力作功,则系统的机械能 就保持不变。 E E E = + = k p 常量 0 d d E E k p + = 四. 能量守恒定律 三. 机械能守恒定律 d d E E k p = −
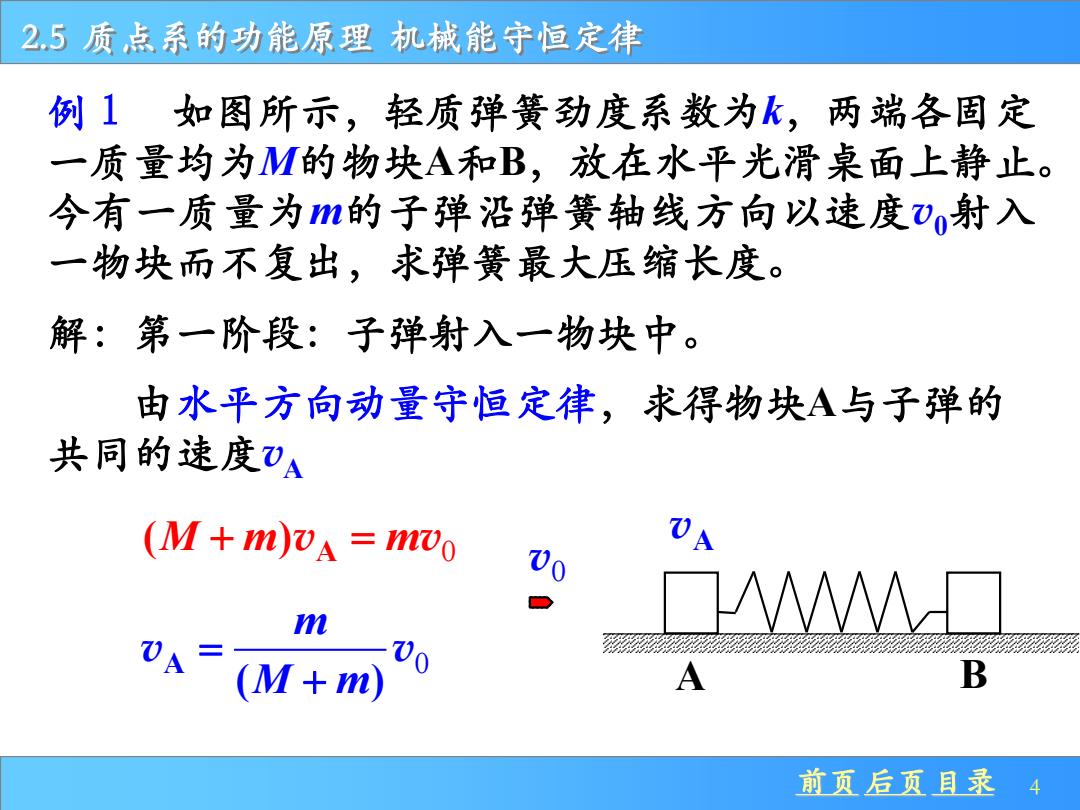
25质点系的功能原理机械能守恒定律 例1如图所示,轻质弹簧劲度系数为k,两端各固定 一质量均为M的物块A和B,放在水平光滑桌面上静止。 今有一质量为m的子弹沿弹簧轴线方向以速度v0射入 一物块而不复出,求弹簧最大压缩长度。 解:第一阶段:子弹射入一物块中。 由水平方向动量守恒定律,求得物块A与子弹的 共同的速度V4 (M+m)v=mvo 0 m % )A=(M+m) A B 前页后页且录4
前页 后页 目录 4 2.5 质点系的功能原理 机械能守恒定律 例1 如图所示,轻质弹簧劲度系数为k,两端各固定 一质量均为M的物块A和B,放在水平光滑桌面上静止。 今有一质量为m的子弹沿弹簧轴线方向以速度v0射入 一物块而不复出,求弹簧最大压缩长度。 A B 解:第一阶段:子弹射入一物块中。 A 0 ( ) m M m = + v v v0 vA 由水平方向动量守恒定律,求得物块A与子弹的 共同的速度vA A 0 ( ) M m m + = v v
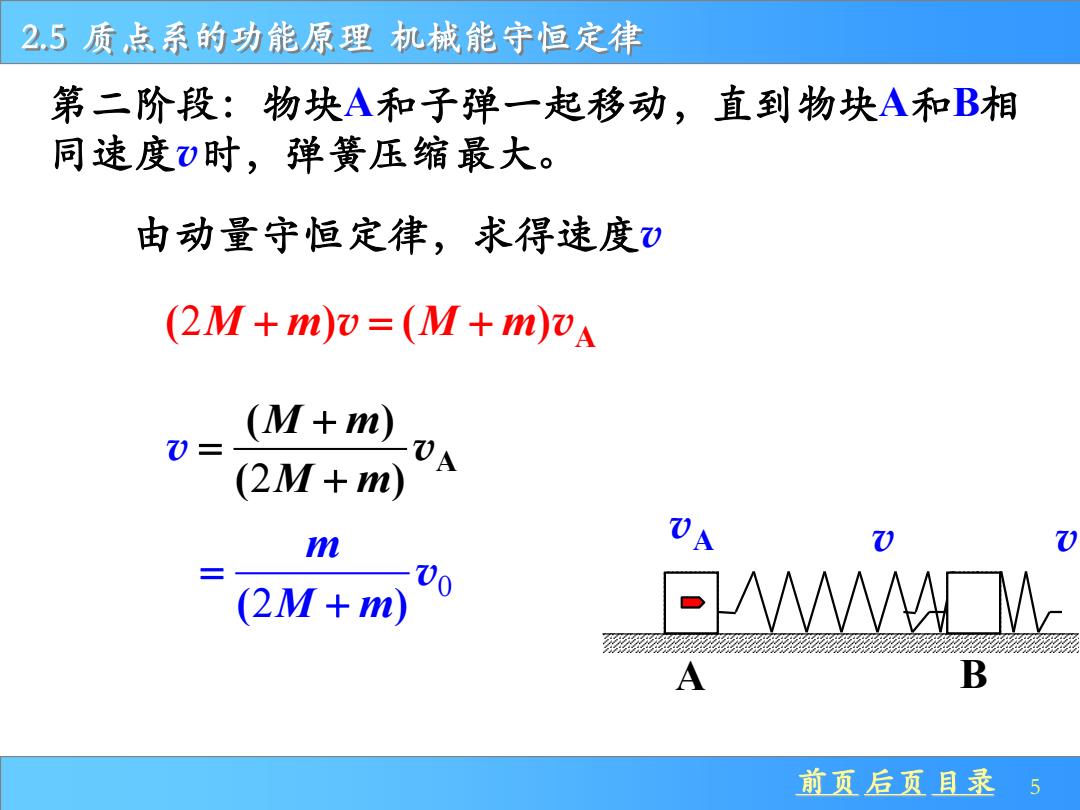
2.5质点系的功能原理机械能守恒定律 第二阶段:物块A和子弹一起移动,直到物块A和B相 同速度)时,弹簧压缩最大。 由动量守恒定律,求得速度) (2M+m)v=(M+m)vA (M+m) (2M+m) n (2M+m) 00 A B 前页后页目录5
前页 后页 目录 5 2.5 质点系的功能原理 机械能守恒定律 第二阶段:物块A和子弹一起移动,直到物块A和B相 同速度v时,弹簧压缩最大。 2 A ( ) ( ) M m M m + = + v v 0 ( ) 2 m M m = + v A B vA 由动量守恒定律,求得速度v v 2 A ( ) ( ) M m M m + = + v v v

25质点系的功能原理机械能守恒定律 由机械能守恒定律,求得弹簧最大压缩长度xm 2A1( 将)和v代入上式,求得弹簧最大压缩长度 M xm=0√k(M+m)(2M+m) 0 A B 本节完 前页后页目录
前页 后页 目录 6 2.5 质点系的功能原理 机械能守恒定律 由机械能守恒定律,求得弹簧最大压缩长度xm 0 2 m ( )( ) M x m k M m M m = + + v 本节完 将vA和v代入上式,求得弹簧最大压缩长度 1 2 2 A ( ) M m+ v 1 2 2 2 ( ) M m+ v A B vA v 1 2 2 + kxm =