
4.4狭义相对论动力学基础 4.4狭义相对论动力学基础 一.相对论力学的基本方程 1.动量p= 2.相对论力学的基本方程 F= p _d(m) F≠md dt dt 3.质量 mo m= m0一静止质量 质量是相对的, 理论 静止质量最小。 推导 前页后页目录
前页 后页 目录 1 4.4 狭义相对论动力学基础 1.动量 p m= v 3.质量 0 2 2 1 m m c v = − m0—静止质量 2.相对论力学的基本方程 d d p F t = 一. 相对论力学的基本方程 4.4 狭义相对论动力学基础 F ma 质量是相对的, 静止质量最小。 d( ) d m t v = 理论 推导

4.4狭义相对论动力学基础 mo d(mi) m= F- 711 dt dt 1- 火箭w=11.2km/s,m=1.0000000009m 电子)=0.98c,m=5mo 讨论: 1)当<<c时,m→。回到牛顿力学。 2)当v→C时,m→oo。极限速度c。 3)当v=c时,mo=0。光子 前页后页目录2
前页 后页 目录 2 4.4 狭义相对论动力学基础 0 2 2 1 m m c v = − d d( ) d d p m F t t v = = 讨论: 1)当v<< c 时,m → m0 。回到牛顿力学。 2)当v → c 时,m → 。极限速度c。 3)当v = c 时,m0 = 0。光子 火箭v =11.2km/s,m=1.000 000 000 9m0 电子v =0.98c,m=5m0

4.4狭义相对论动力学基础 二.质量和能量的关系 1.相对论动能 Ey me2-moc2 ds Fds dEk dt Fdt dp Ek=∫dEk=∫odp=op-∫pdo e mo”=dw 前页后页目录3
前页 后页 目录 3 4.4 狭义相对论动力学基础 1.相对论动能 2 2 E mc m c k = − 0 二. 质量和能量的关系 d d s t v = d d F s F t = d k d E p = E E k k = d = vdp = − v v p pd 2 0 2 2 1 / m c v v = − 2 0 2 0 2 2 1 / m c m c v c = − − 0 0 2 2 1 d / m c v v v v − −
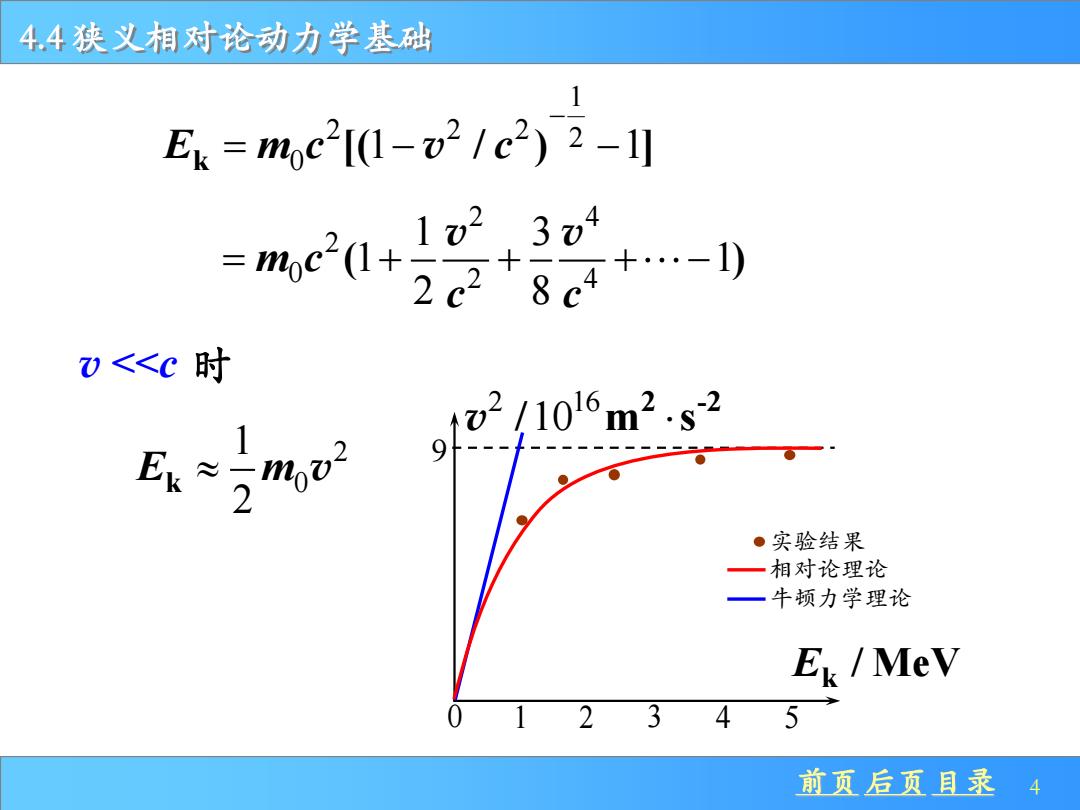
4.4狭义相对论动力学基础 Ek=mc2I1-21c2)2-l川 v<<c时 2/1016m2.s2 ●实验结果 一相对论理论 一牛顿力学理论 EL/MeV 12345 前页后页目录4
前页 后页 目录 4 4.4 狭义相对论动力学基础 v <<c 时 实验结果 相对论理论 牛顿力学理论 k E / MeV 2 16 10 2 -2 v / m s 9 0 1 2 3 4 5 2 4 2 0 2 4 1 3 1 1 2 8 m c ( ) c c v v = + + + − 1 2 2 2 2 0 1 1 k E m c c [( / ) ] v − = − − 2 0 1 2 E m k v

4.4狭义相对论动力学基础 Ek mc2-moc2 2.相对论能量E=mc2 质能关系 3.静能 Eo=moc2 能量守恒 ∑E,-∑m,c2=常量 质量守恒∑m:=常量 前页后页目录5
前页 后页 目录 5 4.4 狭义相对论动力学基础 2 2 E mc m c k = − 0 3.静能 2 E m c 0 0 = 2.相对论能量 2 E mc = 质能关系 能量守恒 2 i i i i E m c = =常量 质量守恒 i i m =常量

4.4狭义相对论动力学基础 讨论: 1.静止物体蕴涵着巨大的静能。 2.质量是惯性的量度,也是总能量的量度。 3.系统能量发生变化时,质量也有相应的变化。 4.孤立系统,总能量守恒时,总质量也守恒。 前页后页目录6
前页 后页 目录 6 4.4 狭义相对论动力学基础 讨论: 1. 静止物体蕴涵着巨大的静能。 2. 质量是惯性的量度,也是总能量的量度。 3. 系统能量发生变化时,质量也有相应的变化。 4. 孤立系统,总能量守恒时,总质量也守恒

4.4狭义相对论动力学基础 三.动量和能量的关系 动量和能量关系式E2=E+pc2 上式推导:, e2moc2 E pc 1-21c2 上式两边平方,去分母 Eo (mc2)2-1m2o2c2=(mc2)2 mc2→E,n→p,c2→Eo E2-p2c2=E 前页后页目录7
前页 后页 目录 7 4.4 狭义相对论动力学基础 上式两边平方,去分母 E E0 pc 三. 动量和能量的关系 动量和能量关系式 上式推导: 2 mc 2 0 2 2 1 / m c v c = − 2 2 2 2 E E p c = + 0 2 2 2 2 2 2 2 0 ( ) ( ) mc m c m c − = v 2 mc E → 2 2 2 2 E p c E − = 0 , m p v → 2 0 0 , m c E →

4.4狭义相对论动力学基础 光子能量 E=hv E=E+p2c2 pe 光子质量 E m= e2 光子动量 h = λ p=mc 前页后页目录8
前页 后页 目录 8 4.4 狭义相对论动力学基础 光子能量 光子质量 光子动量 2 2 2 E E p c pc = + = 0 E h = 2 E m c = h p = p mc =

4.4狭义相对论动力学基础 例1原子核的结合能。已知质子和中子的质量分别为 mp=1.00728u,和m=1.00866u,两个质子和两个中 子组成一氦核H实验测得氦核的质量为m=4.001 50u。计算形成一个氦核放出的能量。(1u=1.660×10 27kg)P158例题3 解:形成氨核之前总质量 m=2m,+2m.=4.03188u 原子核的质量亏损 △m=m-mA=0.03038u =0.03038×1.660×10-27kg 前页后页且录9
前页 后页 目录 9 4.4 狭义相对论动力学基础 例1 原子核的结合能。已知质子和中子的质量分别为 mp =1.007 28u,和mn =1.008 66u,两个质子和两个中 子组成一氦核 ,实验测得氦核的质量为mA=4.001 50u。计算形成一个氦核放出的能量。(1u=1.66010- 27kg) P158例题3 4 2He 解:形成氦核之前总质量 原子核的质量亏损 2 2 4 031 88 p n m m m = + = . u 0 030 38 A m m m = − = . u27 0 030 38 1 660 10 . . kg − =

4.4狭义相对论动力学基础 根据质能关系 △E=△mc2 =0.03038×1.660×10-27×(3×108)2 =0.4539×10-1(J) 结合1mol氦核时放出能量 △E=0.4539×10-11×6.022×1023 =2.733×1012(J 相当于100吨煤燃烧时放出的热量。 本题完 前页后页目录10
前页 后页 目录 10 4.4 狭义相对论动力学基础 根据质能关系 2 E mc = 27 8 2 0 030 38 1 660 10 3 10 . . ( ) − = 结合1mol氦核时放出能量 12 = 2 733 10 . (J) 相当于100吨煤燃烧时放出的热量。 本题完 11 0 453 9 10 . (J) − = 11 23 E 0 453 9 10 6 022 10 . . − =