江苏大学：《大学物理》课程教学资源（PPT课件）第一章 力和运动 1.3 相对运动 常见力和基本力

1.3相对运动常见力和基本力 1.3相对运动常见力和基本力 一.相对运动 行星运动的描述 前页后页目录1

前页 后页 目录 1 1.3 相对运动 常见力和基本力 行星运动的描述 1.3 相对运动 常见力和基本力 一. 相对运动

1.3相对运动常见力和基本力 运动是绝对的，但运动的描述是相对的。 位置坐标、速度、加速度的变换关系？ 前页后页目录2

前页 后页 目录 2 1.3 相对运动 常见力和基本力 运动是绝对的，但运动的描述是相对的。 位置坐标、速度、加速度的变换关系?

13相对运动常见力和基本力 1.伽利略坐标变换 两个参考系中的坐标系分 别为K和K',沿x方向相对作匀 速直线运动。仁0（t'=0)时坐标 y 轴和原点都重合。任意t（=t') 时，质点运动到P处 F=+ =-R 前页后页目录3

前页 后页 目录 3 1.3 相对运动 常见力和基本力 o y x z o  z  x  y  r r  R P 1. 伽利略坐标变换 两个参考系中的坐标系分 别为K和K' ，沿x方向相对作匀 速直线运动。t=0（t'=0）时坐标 轴和原点都重合。任意t（=t'） 时，质点运动到P处 r r R = + r r R  = − v

13相对运动常见力和基本力 F=+ F=xi+yj+ak r'=xi'+yi+a'k R=vti 伽利略坐标变换式 x=x+ut x'=x-ut y=p y=y 0 X z=i" z'=z t=t' t'=t 前页后页目录4

前页 后页 目录 4 1.3 相对运动 常见力和基本力 伽利略坐标变换式 x x t  = − v y y  = z z  = t t  = x x t = + v y y =  z z =  t t =  R ti = v r xi yj zk = + + r x i y j z k        = + + r r  o y x z o  z  x  y  R P v r r R = +

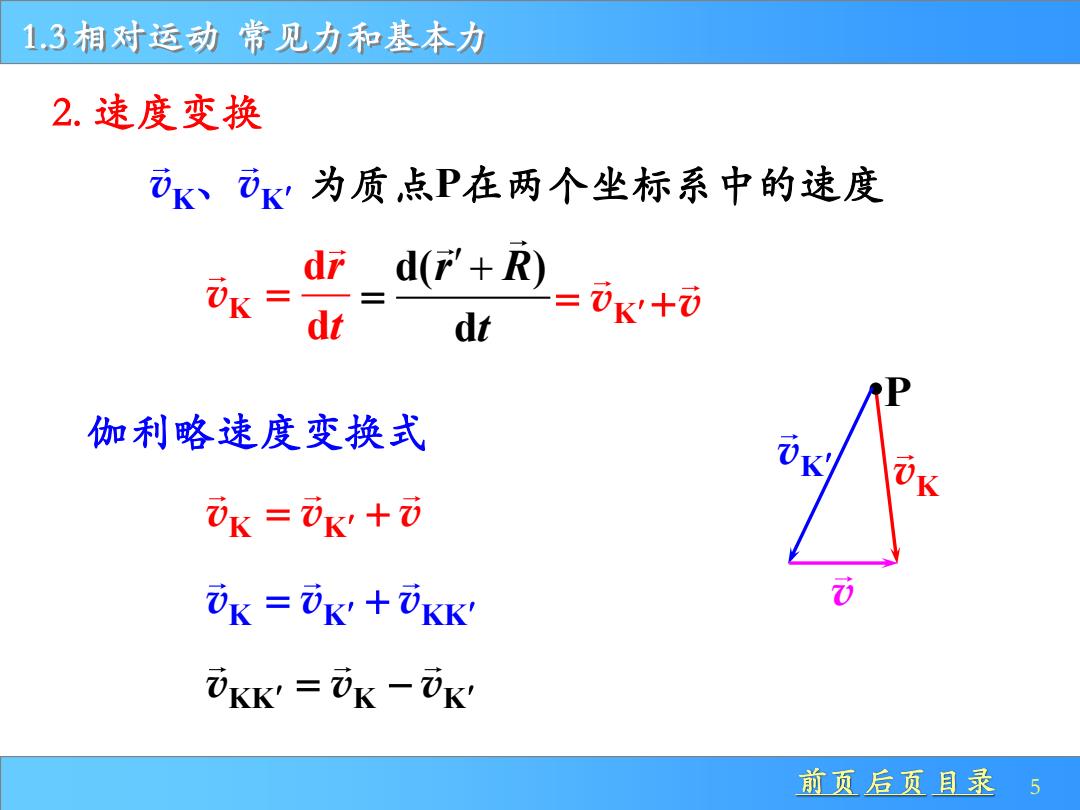
13相对运动常见力和基本力 2.速度变换 K⑦K'为质，点P在两个坐标系中的速度 dr d('+R) dt dt =k+⑦ 伽利略速度变换式 iK=⑦K+0 UK =UK'+UKK' UKK=UK-UK 前页后页目录5

前页 后页 目录 5 1.3 相对运动 常见力和基本力 dt = vK P 2. 速度变换 为质点P在两个坐标系中的速度 K d d r t v = d( ) r R  + 伽利略速度变换式 v v v K K = + vK v v v K K 、  v v v K K KK = +  = vK +v v v v KK K K   = −

13相对运动常见力和基本力 3.加速度变换 KdK'为质，点P在两个坐标系中的加速度 Uk =Uk+ dik-diK dt dt ak ak'+akk' 前页后页目录6

前页 后页 目录 6 1.3 相对运动 常见力和基本力 3. 加速度变换 v v v K K = + d d K K d d d d t t t  = + v v v K K KK a a a = +  a a K K 、  为质点P在两个坐标系中的加速度

13相对运动常见力和基本力 二.常见力 1.重力 北极 G=mg 南极 前页后页目录7

前页 后页 目录 7 1.3 相对运动 常见力和基本力 北极 南极 mgP  o o  F 1.重力 G mg = 二. 常见力

13相对运动常见力和基本力 2.弹力 由形变而产生的欲使物体恢复其原来形状的力。 大小：与物体形变有关。 方向：与使物体发生形变的外力方向相反。 1)物体间的正压力 方向：垂直于接触面指向对方。 前页后页目录8

前页 后页 目录 8 1.3 相对运动 常见力和基本力 2.弹力 由形变而产生的欲使物体恢复其原来形状的力。 大小：与物体形变有关。 方向：与使物体发生形变的外力方向相反。 1)物体间的正压力 方向：垂直于接触面指向对方。 N N

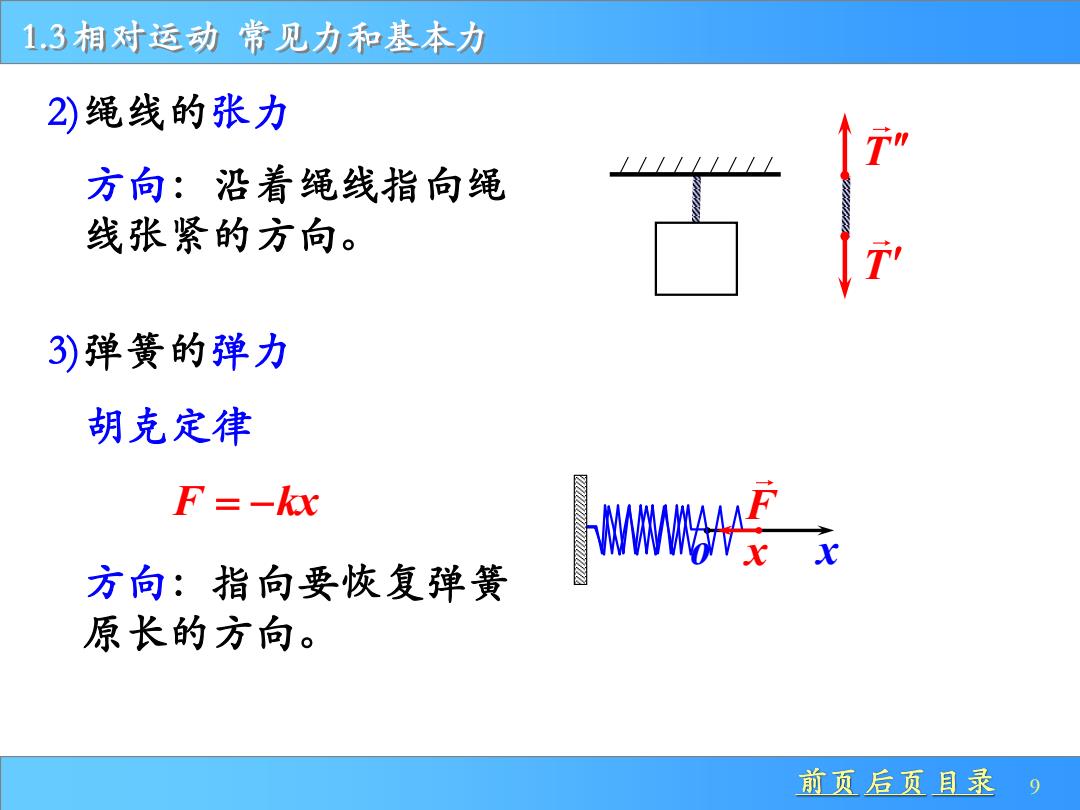
1.3相对运动常见力和基本力 2)绳线的张力 方向：沿着绳线指向绳 线张紧的方向。 1' 3)弹簧的弹力 胡克定律 F=-kx 方向：指向要恢复弹簧 原长的方向。 前页后页目录9

前页 后页 目录 9 1.3 相对运动 常见力和基本力 2)绳线的张力 方向：沿着绳线指向绳 线张紧的方向。 T T 3)弹簧的弹力 胡克定律 F kx = − 方向：指向要恢复弹簧 原长的方向。 o x F x

13相对运动常见力和基本力 3.摩擦力 相互接触的物体有相对运动或有相对运动趋势 时，接触面上产生的阻碍相对运动的力。 滑动摩擦力 fi=LN 4为滑动摩擦系数 静摩擦力 0<f、<天max 最大静摩擦力∫max=4,N 山为静摩擦系数 4<4<1 前页后页目录10

前页 后页 目录 10 1.3 相对运动 常见力和基本力 3.摩擦力 相互接触的物体有相对运动或有相对运动趋势 时，接触面上产生的阻碍相对运动的力。 滑动摩擦力 k k f N =  k为滑动摩擦系数 静摩擦力 0 s smax   f f 最大静摩擦力 smax s f N =  s为静摩擦系数 1   k s  