
2,1质点系的肉力和外力质心心质心运动定理 2.1质点系的内力和外力 质心质心运动定理 一.质点系的内力和外力 质点系内各个质点之间的相互作用称为内力。质 点系所有内力的矢量和为零。 系统外物体对系统内质点的作用称为外力。 前页后页且录1
前页 后页 目录 1 2.1 质点系的内力和外力 质心 质心运动定理 一. 质点系的内力和外力 2.1 质点系的内力和外力 质心 质心运动定理 质点系内各个质点之间的相互作用称为内力。质 点系所有内力的矢量和为零。 系统外物体对系统内质点的作用称为外力

2,1质点系的内力和外力质心质心运动定理 二.质心 系统质量分布的中心 前页后页目录2
前页 后页 目录 2 2.1 质点系的内力和外力 质心 质心运动定理 系统质量分布的中心 二. 质心

2,1质点系的肉力和外力质心心质心运动定理 1.质心的位置矢量 N个质,点m1,m2,…,i…mN m=∑m 所,2,…,,… 质量连续分布的物体 ∫rdm -am 直角坐标系中衣=xi+j+k 前页后页目录3
前页 后页 目录 3 2.1 质点系的内力和外力 质心 质心运动定理 1 2 , , , ,i N r r r r 1.质心的位置矢量 c i i i m r r m = 质量连续分布的物体 c d d r m r m = N个质点 1 2 , , , , m m m m i N c c c c 直角坐标系中 r = x i y j z k + + m m = i

2,1质点系的内力和外力质心心质心心运动定理 2.直角坐标系中质心的位置坐标 N个质点%,2,…,mi,…mN mi(xi,yi,ti) ∑m片 前页后页目录4
前页 后页 目录 4 2.1 质点系的内力和外力 质心 质心运动定理 ( , , ) m x y z i i i i 2.直角坐标系中质心的位置坐标 c i i i m x x m = c i i i m y y m = c i i i m z z m = N个质点 1 2 , , , , m m m m i N
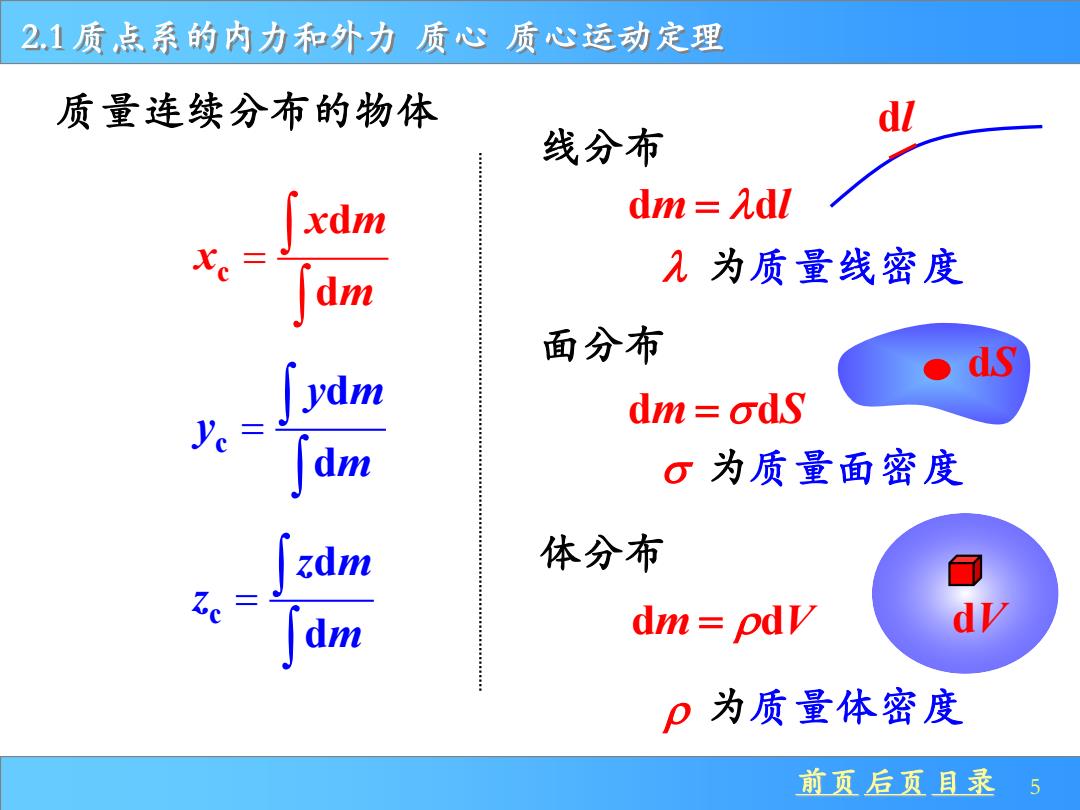
2,1质点系的内力和外力质心质心运动定理 质量连续分布的物体 dl 线分布 xdm dm Adl 九为质量线密度 面分布 dm odS σ为质量面密度 体分布 dm pdy p为质量体密度 前页后页目录 5
前页 后页 目录 5 2.1 质点系的内力和外力 质心 质心运动定理 c d d x m x m = c d d y m y m = c d d z m z m = 线分布 d d m l = 面分布 d d m S = 体分布 d d m V = dl dS dV 为质量线密度 为质量面密度 为质量体密度 质量连续分布的物体

2,1质点系的内力和外力质心质心运动定理 讨论: 1)匀质规则物体的质心在几何中心。 2)刚体的质心相对自身位置不变。 3)质心和重心是两个不同的概念。 物体几何尺寸不大时,质心与重心 位置重合。 前页后页目录6
前页 后页 目录 6 2.1 质点系的内力和外力 质心 质心运动定理 讨论: 1)匀质规则物体的质心在几何中心。 2)刚体的质心相对自身位置不变。 3)质心和重心是两个不同的概念。 物体几何尺寸不大时,质心与重心 位置重合

2,1质点系的肉力和外力质心心质心运动定理 例1求腰长为的匀质等腰直角三角形薄板的质心 位置。P55例题1 解:建立如图所示坐标系。根据 对称性,薄板质心就在X轴上。设 dx 薄板的质量面密度为σ,面积元 宠 X dm o2xdx 质心X坐标 ∫dm 2ox'dx 2 x.am 2oxdx 本题完 前页后页且录7
前页 后页 目录 7 2.1 质点系的内力和外力 质心 质心运动定理 设 薄板的质量面密度为,面积元 根据 对称性,薄板质心就在x轴上。 例1 求腰长为a 的匀质等腰直角三角形薄板的质心 位置。P55例题1 x dx o x y 2 a 解:建立如图所示坐标系。 d d m x x = 2 质心x坐标 c d d x m x m = 2 0 d 2 a x x = 本题完 2 2 0 2 d a x x 2 3 = a

2,1质点系的内力和外力质心质心运动定理 三,质心运动定理 限-兴 1.质心速度 d d方 ∑m,t_m@! dt ∑m,∑m; 2.质心加速度 00 ic= ∑m,正证_",a dt ∑m: ∑m; 前页后页目录8
前页 后页 目录 8 2.1 质点系的内力和外力 质心 质心运动定理 质心位矢 c i i i m r r m = 1.质心速度 c c d d r t v = d d i i i r m t m = i i i m m = v 2.质心加速度 c c d d a t = v d d i i i m t m = v i i i m a m = 三. 质心运动定理

2,1质点系的内力和外力质心心质心心运动定理 每个质点应用牛顿第二定律 +f2+fi3+…+无m=m,d 2+f1+f23+…+f2n=d2 En+方n+fn2+…+fnn-l=mndn 以上各式相加,考虑到作用力与反作用力 f,+f元=0 前页后页且录9
前页 后页 目录 9 2.1 质点系的内力和外力 质心 质心运动定理 每个质点应用牛顿第二定律 F f f f m a 1 12 13 1 1 1 + + + + = n F f f f m a 2 21 23 2 2 2 + + + + = n F f f f m a n n n nn n n + + + + = 1 2 1− 以上各式相加,考虑到作用力与反作用力 0 ij ji f f + =

21质点系的内力和外力质心质心运动定理 得∑F;=∑m,a 6 则 m 3.质心运动定理 ∑F;=ma ∑F外力的失量和(不是合外力) 推论:外力的矢量和为零时, 质心加速度为零。 即系统动量守恒 翼 前页后页目录 10
前页 后页 目录 10 2.1 质点系的内力和外力 质心 质心运动定理 得 i i i F m a = 则 c i i i m a a m = 3.质心运动定理 F ma i = c 推论:外力的矢量和为零时, 质心加速度为零。 Fi 外力的矢量和(不是合外力) 即系统动量守恒 Fi m = c i i i m m = v v =常矢量