85带电粒子在电场和磁场中的运动 8.5带电粒子在电场和磁场中的运动 一.洛伦兹力 磁场对运动电荷的作用力。 a.平行于磁场方向运动时 F=0 b.垂直于磁场方向运动时 Fmax =B qo max 前页后页目录 1
8.5 带电粒子在电场和磁场中的运动 前页 后页 目录 1 一. 洛伦兹力 磁场对运动电荷的作用力。 a.平行于磁场方向运动时 B q v b.垂直于磁场方向运动时 B q v Fmax 8.5 带电粒子在电场和磁场中的运动 F = 0 Fmax B q = v

85带电粒子在电场和磁场中的运动 c.任意方向运动时 F=D×B洛仑兹力公式 大小:F=goBsin0 方向:q元×B 1.带电粒子在均匀磁场中的运动 1)初速度与磁场平行F=0 匀速直线运动。 2)初速度与磁场垂直F=qB 匀速圆周运动。 前页后页目录2
8.5 带电粒子在电场和磁场中的运动 前页 后页 目录 2 F F q B = v 洛仑兹力公式 大小: F q B = v sin 方向: q B v B v c.任意方向运动时 1. 带电粒子在均匀磁场中的运动 1) 初速度与磁场平行 2) 初速度与磁场垂直 匀速圆周运动。 匀速直线运动。 F = 0 F q B = v
8.5带电粒子在电场和磁场中的运动 由牛顿运动定律 UoB=m R 轨道半径 R=100 gB 运动周期 T= 2n-2 m Vo gB 前页后页目录 3
8.5 带电粒子在电场和磁场中的运动 前页 后页 目录 3 由牛顿运动定律 轨道半径 运动周期 2 0 0 q B m R = v v m 0 R qB = v 0 2πR T = v 2π m qB =
85带电粒子在电场和磁场中的运动 3)初速度与磁场方向成日角 螺旋运动。 Vol vo cos0 0 7ol vo sin0 螺旋半径R= mvol gB 螺旋周期T= 2πn gB 螺距h=orT 前页后页目录 4
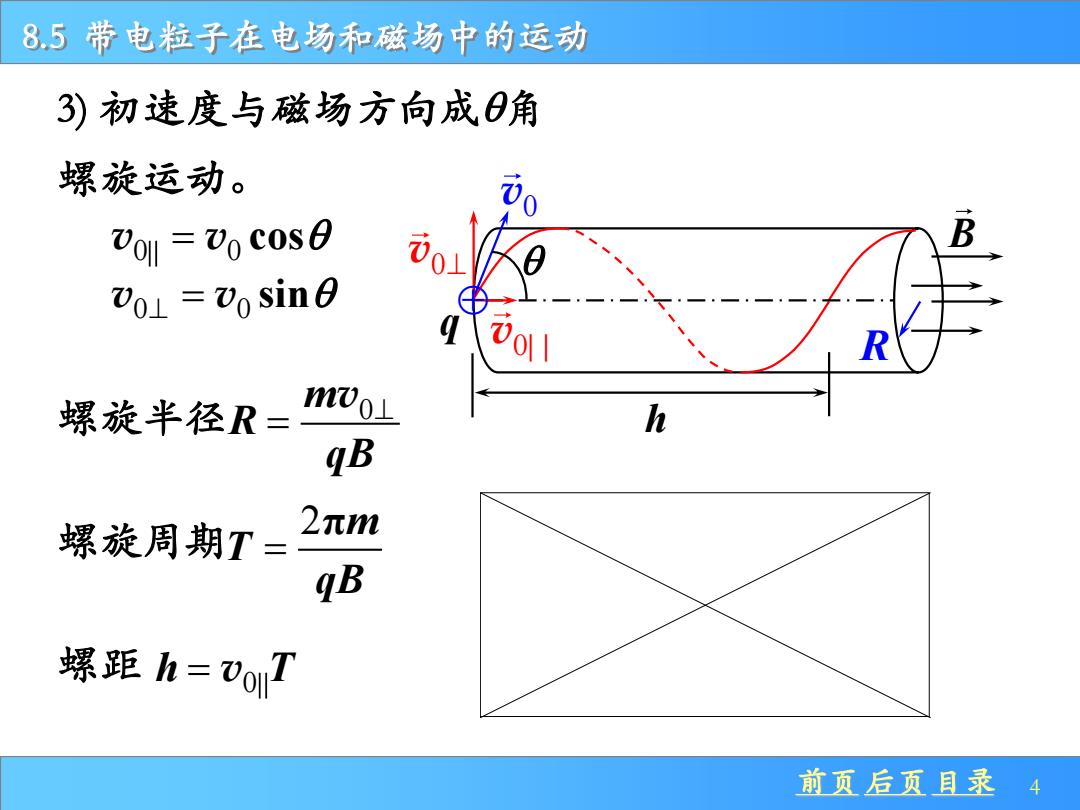
8.5 带电粒子在电场和磁场中的运动 前页 后页 目录 4 3) 初速度与磁场方向成角 v0 B v0⊥ R h q v0| | 螺旋运动。 螺距 m 0 R qB ⊥ = v 0 0 v v = cos 0 0 sin v v ⊥ = 2πm T qB = h T = v0 螺旋半径 螺旋周期

85带电粒子在电场和磁场中的运动 2.带电粒子在非均匀磁场中的运动 前页后页目录5
8.5 带电粒子在电场和磁场中的运动 前页 后页 目录 5 2. 带电粒子在非均匀磁场中的运动
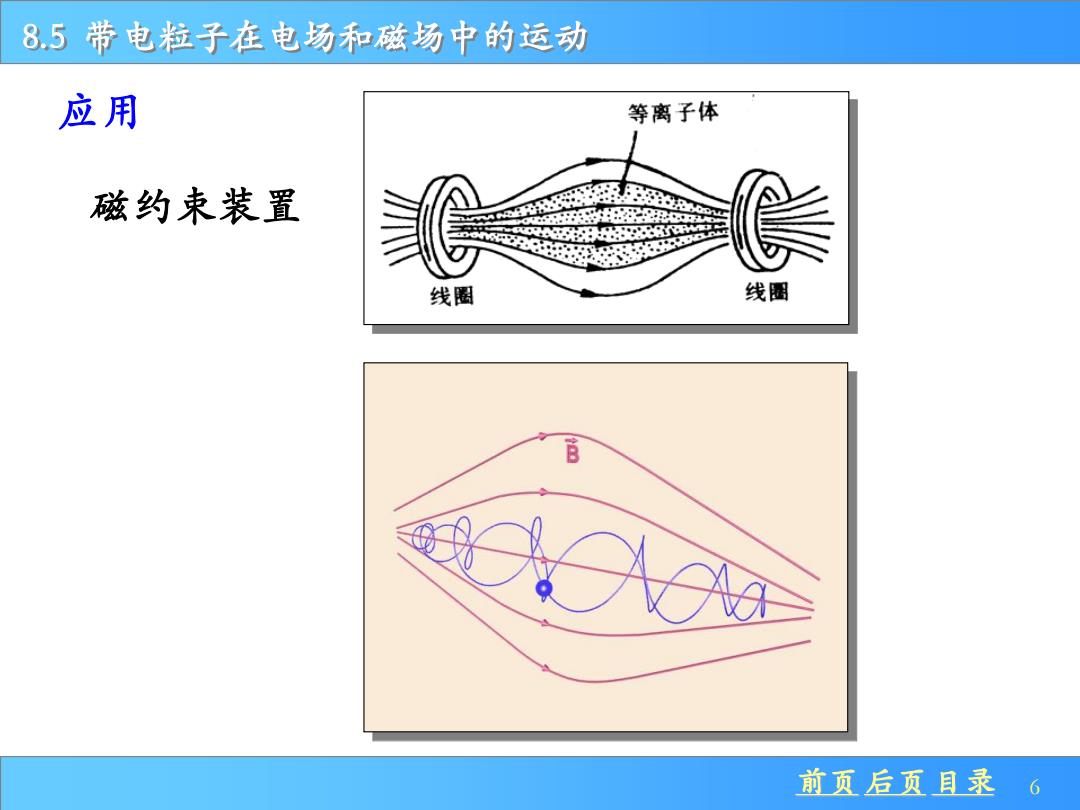
8.5带电粒子在电场和磁场中的运动 应用 等离子体 磁约束装置 线圈 前页后页目录 6
8.5 带电粒子在电场和磁场中的运动 前页 后页 目录 6 磁约束装置 应用
8.5带电粒子在电场和磁场中的运动 二,带电粒子在电磁场中的运动的应用 磁聚焦 0≈0 Vo≈V0 h=V0T 螺距相等 测定荷质比,回旋加速器,质谱仪等 前页后页目录 7
8.5 带电粒子在电场和磁场中的运动 前页 后页 目录 7 螺距相等 磁聚焦 二. 带电粒子在电磁场中的运动的应用 0 v v 0 0 h T = v0 测定荷质比,回旋加速器,质谱仪等
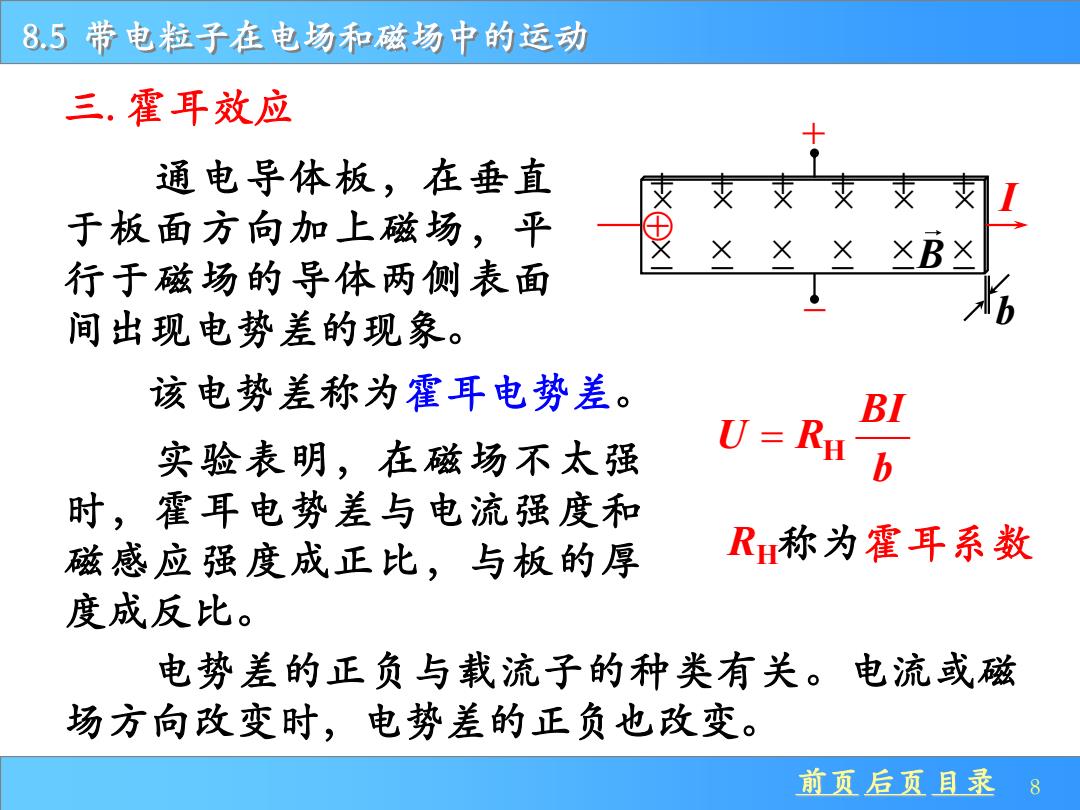
85带电粒子在电场和磁场中的运动 三.霍耳效应 通电导体板,在垂直 支支支支肉1 于板面方向加上磁场,平 行于磁场的导体两侧表面 间出现电势差的现象。 该电势差称为霍耳电势差。 BI 实验表明,在磁场不太强 U=R 时,霍耳电势差与电流强度和 磁感应强度成正比,与板的厚 R称为霍耳系数 度成反比。 电势差的正负与载流子的种类有关。电流或磁 场方向改变时,电势差的正负也改变。 前页后页目录8
8.5 带电粒子在电场和磁场中的运动 前页 后页 目录 8 通电导体板,在垂直 于板面方向加上磁场,平 行于磁场的导体两侧表面 间出现电势差的现象。 三. 霍耳效应 − b + I B + + + + + + − − − − − − 该电势差称为霍耳电势差。 实验表明,在磁场不太强 时,霍耳电势差与电流强度和 磁感应强度成正比,与板的厚 度成反比。 H BI U R b = RH称为霍耳系数 电势差的正负与载流子的种类有关。电流或磁 场方向改变时,电势差的正负也改变

8.5带电粒子在电场和磁场中的运动 霍耳系数推导 载流子受到的洛仑兹力与电 场力平衡时,霍耳电势差将保持 得v= gnbh 不变。 U=vBh Fm=Fe 1 BI qoB=4h ng b U=hoB 霍耳系数 设载流子浓度为n,则电流强度为 R ng 1=12_gnblrodt gnbhv dt dt 本节完 前页后页目录 9
8.5 带电粒子在电场和磁场中的运动 前页 后页 目录 9 载流子受到的洛仑兹力与电 场力平衡时,霍耳电势差将保持 不变。 霍耳系数推导 F F m e = q Bv U q h = U h B = v 设载流子浓度为n,则电流强度为 d d Q I t = d d qnbh t t = v = qnbhv 得 霍耳系数 I qnbh v = U Bh = v 1 BI nq b = 1 RH nq = 本节完