
10.3受迫振动和共振 10.3受迫振动和共振 一.受迫振动 外力持续作用时的振动。 驱动力F=Fc0soat F为驱动力幅值,⊙为驱动力的角频率。 d2x dx 动力学方程m r—¥a +Fo cos@at 令00= k 6=”则 m 2m 前页后页目录 1
前页 后页 目录 1 10.3 受迫振动和共振 一. 受迫振动 外力持续作用时的振动。 驱动力 0 d F F t = cos F0为驱动力幅值,d为驱动力的角频率。 动力学方程 2 2 0 d d d cos d d x x m kx F t t t = − − + 令 0 , 则 k m = 2m = 10.3 受迫振动和共振

10.3受迫振动和共振 +2分 d2x dt2 +0x= dt cs (1)小阻尼时的解 x=Aoe-oi cos(a-82t+)+Acos(@gt+) 衰减项 稳态项 (2)稳定时的解 x=Acos(@at+) 前页后页且录2
前页 后页 目录 2 10.3 受迫振动和共振 2 2 0 2 0 2 d d d cos d d x x F x t t t m + + = (1)小阻尼时的解 2 2 0 0 0 0 d e cos( ') cos( ) t x A t A t − = − + + + 衰减项 稳态项 (2)稳定时的解 d 0 x A t = + cos( )

10.3受迫振动和共振 A= F mV(of-o.2)2+462oa2 o arctan- 260a 6-02 速度0= dx dt =m cos(at++ QaFo Um mV(@-@a2)2+462o 前页后页目录3
前页 后页 目录 3 10.3 受迫振动和共振 0 2 2 2 2 2 0 4 d d ( ) F A m = − + 0 2 2 0 2 d d arc tan = − − 速度 0 2 m d d π cos( ) d x t t v v = = + + 0 2 2 2 2 2 0 4 d m d ( ) F m = − + v
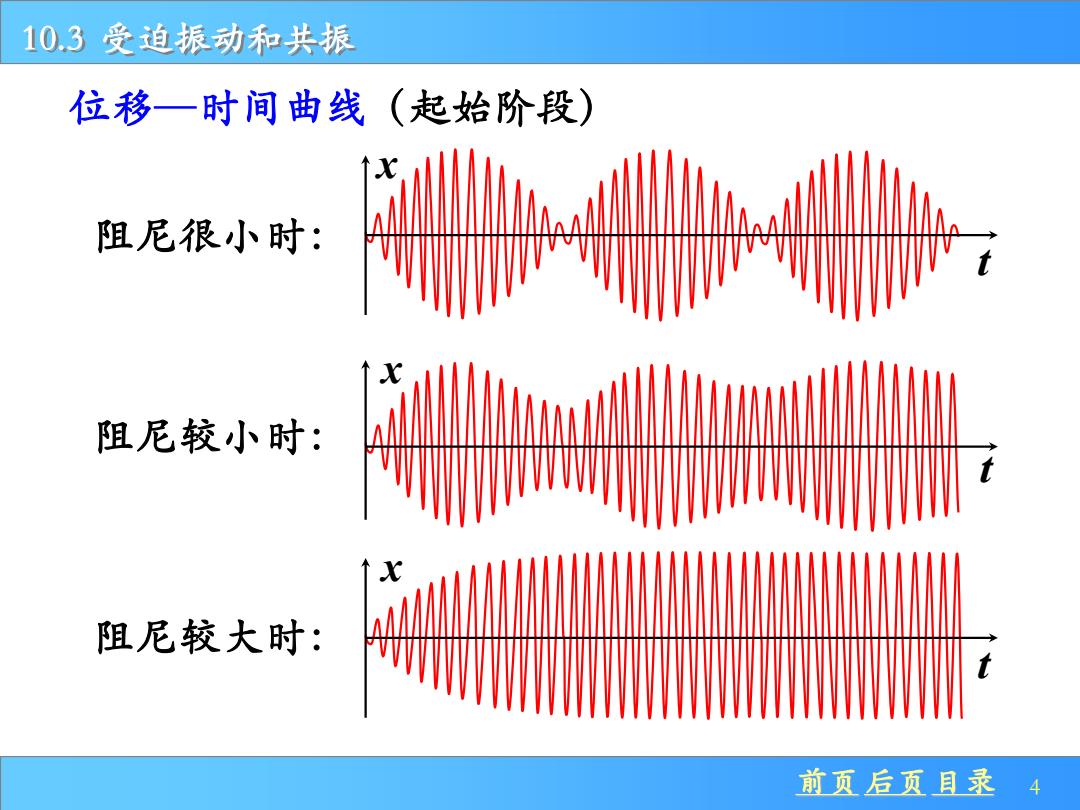
10.3受迫振动和共振 位移一时间曲线(起始阶段) 阻尼很小时: 阻尼较小时: 阻尼较大时: 前页后页目录 4
前页 后页 目录 4 10.3 受迫振动和共振 位移—时间曲线(起始阶段) 阻尼较小时: 阻尼较大时: 阻尼很小时: x t x t x t

103受迫振动和共振 二,共振 位移共振 A !1阻尼=0 ①共振 =V好-262 共振频率越接近 阻尼 固有频率,位移幅振 越大。位移共振频率 0 总小于固有频率。 前页后页目录 5
前页 后页 目录 5 10.3 受迫振动和共振 二. 共振 o 0 A 阻尼=0 阻尼大 阻尼小 位移共振 2 2 0 共振 = − 2 共振频率越接近 固有频率,位移幅振 越大。位移共振频率 总小于固有频率
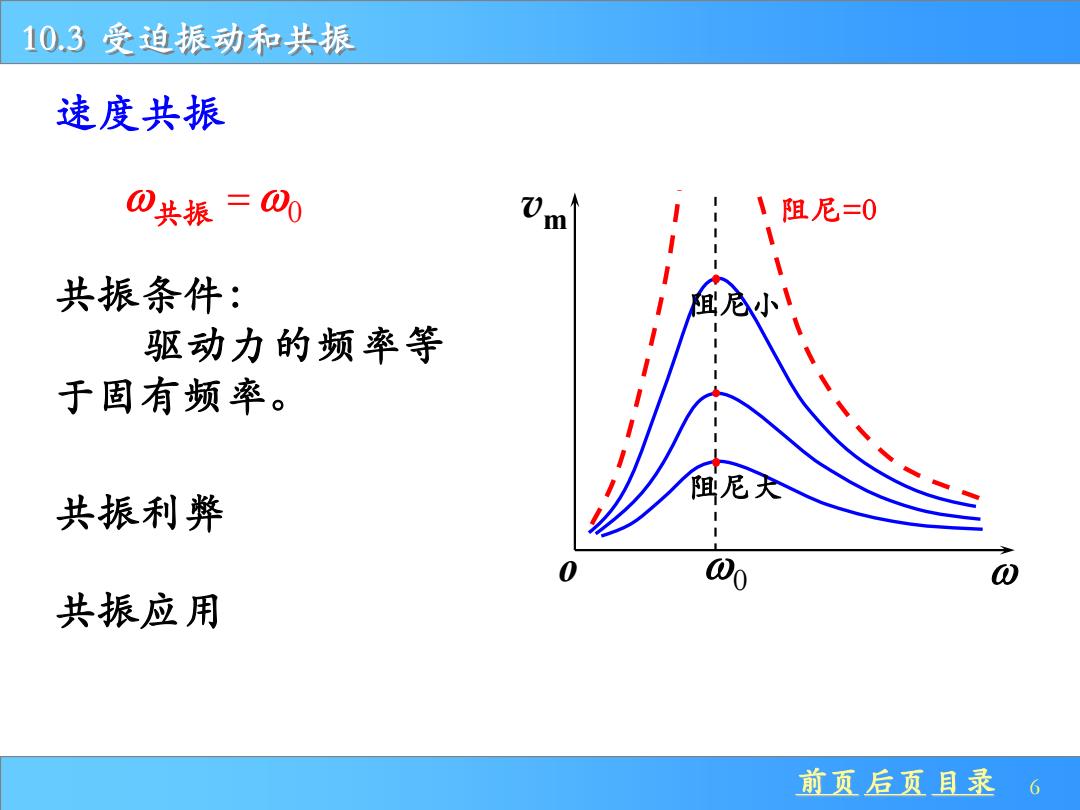
10.3受迫振动和共振 速度共振 0共振=00 1阻尼=0 共振条件: 尼小 驱动力的频率等 于固有频率。 阻尼大 共振利弊 共振应用 前页后页目录 6
前页 后页 目录 6 10.3 受迫振动和共振 速度共振 o 0 vm 阻尼=0 阻尼大 阻尼小 共振 = 0 共振条件: 驱动力的频率等 于固有频率。 共振利弊 共振应用

10.3受迫振动和共振 “鱼洗”之迷 本节完 前页后页目录 7
前页 后页 目录 7 10.3 受迫振动和共振 本节完 “鱼洗”之迷