10.5一维振动的合成 10.5一维振动的合成 频率比1:21:31:42:3 ·●川全同 振幅调节 频率调节 初相调节 显示控制动画控制 前页后页目录 1
前页 后页 目录 1 10.5 一维振动的合成 10.5 一维振动的合成

10.5一维振动的合成 一.同一直线上两个同频率的谐运动的合成 x1=AC0s(t+40) x2=A cos(@t+0) 合位移x=x1+x=Ac0s(0t+4) 合振动是简谐振动 式中A=√A+4+2AA2c0s(0-40) tan= A singo+2 singo 4 cosdo+2 coso 前页后页目录 2
前页 后页 目录 2 10.5 一维振动的合成 合位移 1 2 0 x x x A t = + = + cos( ) 式中 2 2 1 2 1 2 20 10 A A A A A = + + − 2 cos( ) 合振动是简谐振动 1 10 2 20 0 1 10 2 20 sin sin tan cos cos A A A A + = + 一. 同一直线上两个同频率的谐运动的合成 1 1 10 x A t = + cos( ) 2 2 20 x A t = + cos( )

10.5一维振动的合成 旋转失量法求合振动 分振动 x=A cos(ot+do) x2=A2c0s(0t+420) 合振动 x=Acos(@t+) 前页后页目录3
前页 后页 目录 3 10.5 一维振动的合成 A A1 A2 o x 1 1 10 x A t = + cos( ) 2 2 20 x A t = + cos( ) 合振动 0 x A t = + cos( ) 旋转矢量法求合振动 分振动
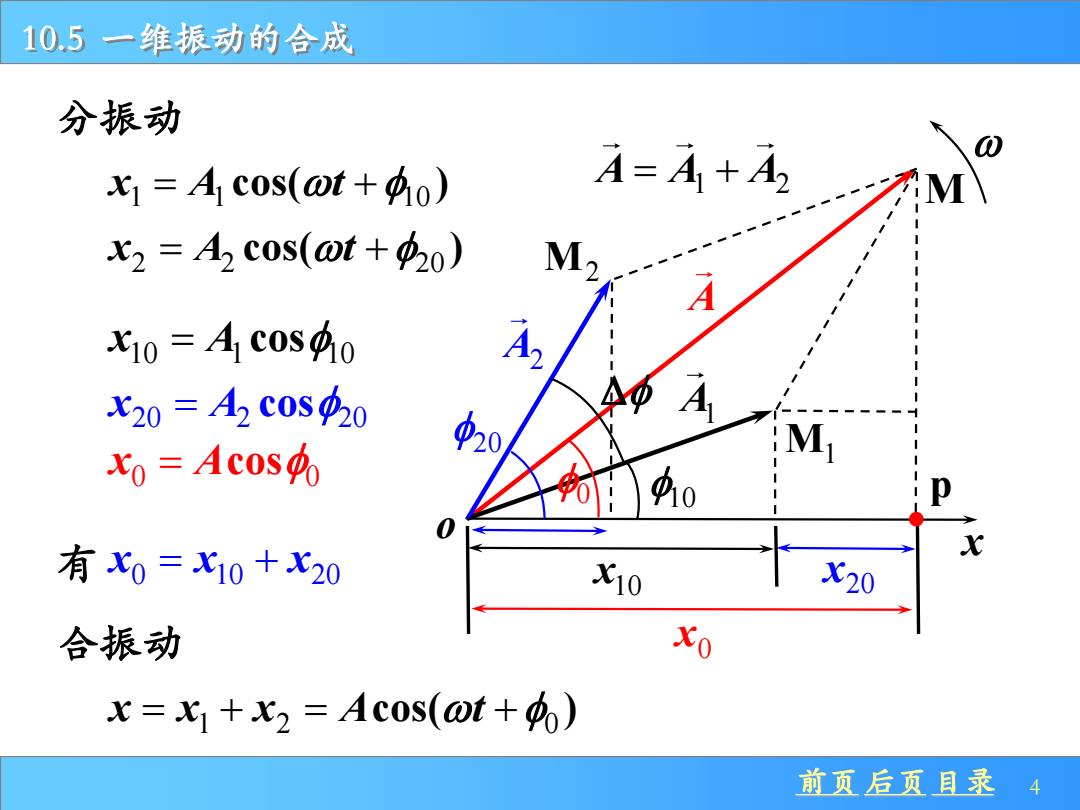
10.5一维振动的合成 分振动 女1=Ac0s(ot+4o) 4=4+4 升M x2=A2c0s(ot+420) M, A X10=AC0s40 x20=A2C0s420 20 M xo =Acoso p 有x0=X10+X20 X10 X20 合振动 xo x=X1+x2=Ac0s(0t+4) 前页后页目录4
前页 后页 目录 4 10.5 一维振动的合成 10 1 10 x A = cos 20 2 20 x A = cos 0 0 x A = cos 有 0 10 20 x x x = + M M2 A A A = +1 2 A M1 p x A2 A1 10 10 x o 0 20 0 x 20 x 1 1 10 x A t = + cos( ) 2 2 20 x A t = + cos( ) 分振动 合振动 0 = + A t cos( ) 1 2 x x x = +
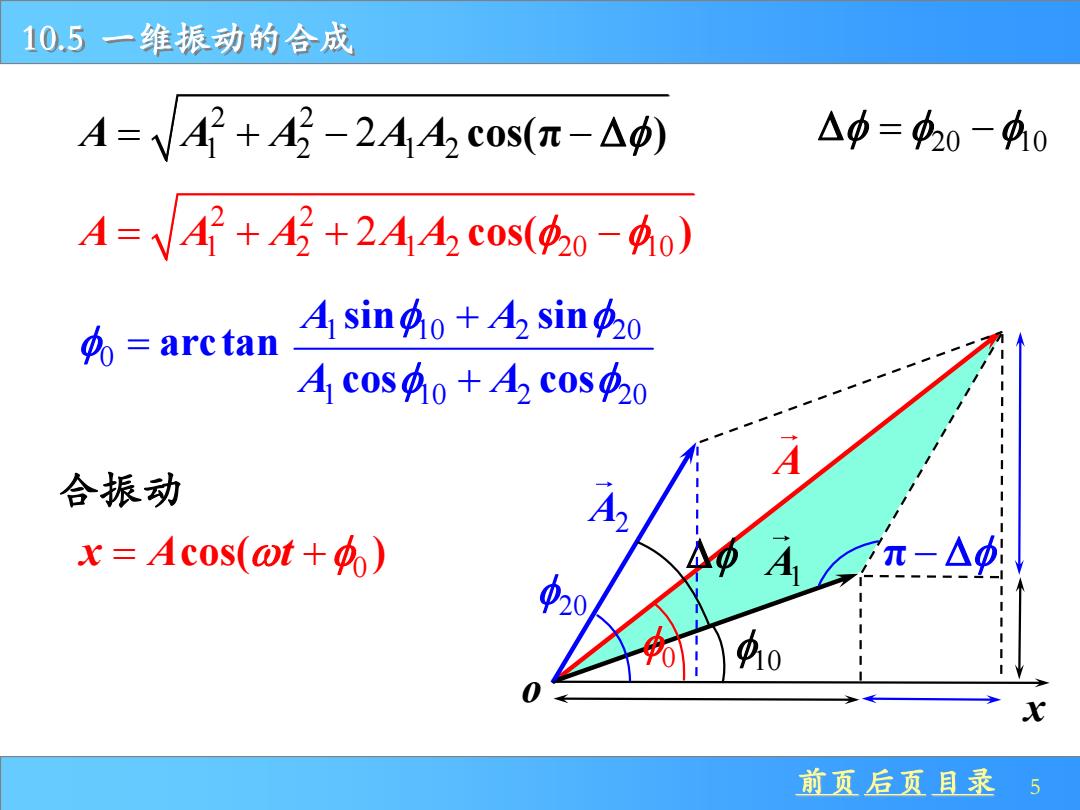
10.5一维振动的合成 A=VA+A-2AAc0s(π-△) △p=420-410 A=VA2+A+2AA2c0s(40-40) arctan A singo+2 sing2o Ac0s40+A2c0s420 合振动 x=Acos(@t+) 20 910 0 前页后页且录5
前页 后页 目录 5 10.5 一维振动的合成 A A2 A1 10 o 0 20 2 2 1 2 1 2 A A A A A = + − − 2 cos(π ) 2 2 1 2 1 2 20 10 A A A A A = + + − 2 cos( ) 0 = arc tan x π − 0 x A t = + cos( ) 合振动 20 10 = − 1 10 2 20 A A cos cos + 1 10 2 20 A A sin sin +

10.5一维振动的合成 讨论: (1)同相△φ=4-4=0-40=士2km k=0,1,2,… 则A=A+A2合振幅最大。 (②)反相△=4-4=40-40=±(2k-1)m k=1,2,… 则A=A-A21 合振幅最小。振幅零表示静止。 (3)一般情况,合振幅介于A1+A2和A1A2之间。 前页后页目录6
前页 后页 目录 6 10.5 一维振动的合成 讨论: (1) 同相 A1 A2 2 1 20 10 = − = − = 2kπ k=0,1,2,… 则 合振幅最大。 (2) 反相 A1 A2 2 1 20 10 = − = − = − ( ) 2 1 k π k=1,2,… 合振幅最小。振幅零表示静止。 (3) 一般情况,合振幅介于A1+A2和|A1-A2 |之间。 A A A = +1 2 则 1 2 A A A = − | |
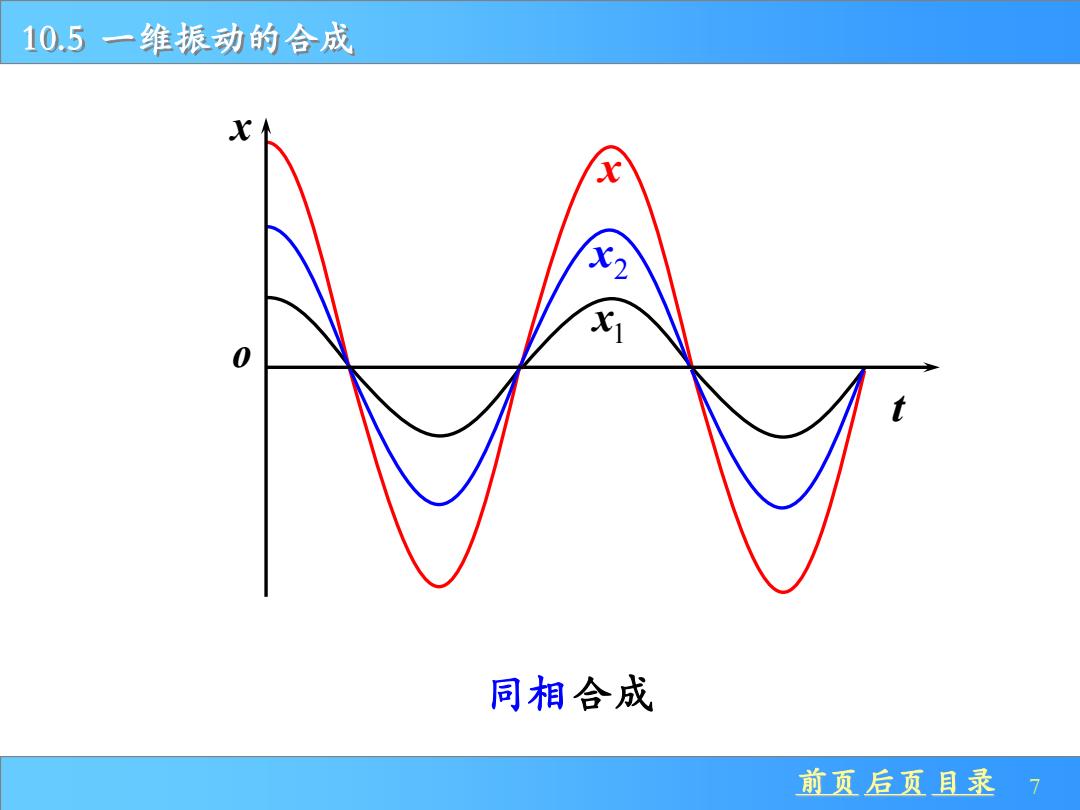
10.5一维振动的合成 同相合成 前页后页目录 7
前页 后页 目录 7 10.5 一维振动的合成 x t o x 2 x 1 x 同相合成

10.5一维振动的合成 反相合成 前页后页目录 8
前页 后页 目录 8 10.5 一维振动的合成 x o x 2 x 1 x t 反相合成

10.5一维振动的合成 一般合成 前页后页目录 9
前页 后页 目录 9 10.5 一维振动的合成 x o x 2 x 1 x t 一般合成

10.5一维振动的合成 二.同一直线上两个不同频率的谐运动的合成拍 假设两分振动表达式为 x=Acos(@t+o) x2=Ac0s(02t+4) 合振动方程 x=2A0y9,)ox%于@1+4) 01≈02)01>02 前页后页目录10
前页 后页 目录 10 10.5 一维振动的合成 12,1>2 假设两分振动表达式为 合振动方程 1 2 2 1 0 2 2 2 x A t t cos( ) cos( ) − + = + 1 1 0 x A t = + cos( ) 2 2 0 x A t = + cos( ) 二. 同一直线上两个不同频率的谐运动的合成 拍