
第三章次数分布和平均数、变异数 第一节总体及其样本 第二节次数分布 第三节平均数 第四节变异数 第五节理论总体(群体)的平均数和标准差
第三章 次数分布和平均数、变异数 第一节 总体及其样本 第二节 次数分布 第三节 平均数 第四节 变异数 第五节 理论总体(群体)的平均数和标准差

第一节总体及其样本 ●总体(population)-具有共同性质的个体所组成的集团. 有限总体一总体所包含的个体数目有无穷多个. 无限总体-由有限个个体构成的总体. ●观察值(observation)-每一个体的某一性状、特性的测 定数值. ● 变数(variable)-观察值集合起来,称为总体的变数。 变数又称为随机变数(random variable)
第一节 总体及其样本 ⚫ 总体( population ) - 具有共同性质的个体所组成的集团. 有限总体-总体所包含的个体数目有无穷多个 . 无限总体-由有限个个体构成的总体. ⚫ 观察值( observation ) -每一个体的某一性状、特性的测 定数值. ⚫ 变数( variable ) -观察值集合起来,称为总体的变数。 变数又称为随机变数(random variable)

●样本(sample)-从总体中抽取若干个个体的集合称为样 本(sample)。 ●统计数(statistic)-测定样本中的各个体而得的样本特征 数,如平均数等,称为统计数(statistic)。 ●随机样本(random sample)-从总体中随机抽取的样本称 为随机样本(random sample) ●样本容量(sample size)-样本中包含的个体数称为样本容 量或样本含量(sample size)
⚫样本( sample ) -从总体中抽取若干个个体的集合称为样 本(sample)。 ⚫统计数( statistic ) -测定样本中的各个体而得的样本特征 数,如平均数等,称为统计数(statistic)。 ⚫随机样本( random sample ) -从总体中随机抽取的样本称 为随机样本(random sample) ⚫样本容量( sample size ) -样本中包含的个体数称为样本容 量或样本含量(sample size)

第二节次数分布 一、试验资料的性质与分类 二、次数分布表 三、次数分布图
第二节 次数分布 一、试验资料的性质与分类 二、次数分布表 三、次数分布图

一、试验资料的性质与分类 (一)数量性状资料 (二)质量性状资料
一、试验资料的性质与分类 (一) 数量性状资料 (二) 质量性状资料

(一) 数量性状资料 数量性状(quantitative trait)的度量有计数和量测两种 方式,其所得变数不同。 1.不连续性或间断性变数(discontinuous or discrete vatiable)指用计数方法获得的数据。 2.连续性变数(continuous variable)指称量、度量或测 量方法所得到的数据,其各个观察值并不限于整数,在两个 数值之间可以有微量数值差异的第三个数值存在
(一) 数量性状资料 数量性状(quantitative trait)的度量有计数和量测两种 方式,其所得变数不同。 1. 不连续性或间断性变数( discontinuous or discrete variable ) 指用计数方法获得的数据。 2. 连续性变数( continuous variable ) 指称量、度量或测 量方法所得到的数据,其各个观察值并不限于整数,在两个 数值之间可以有微量数值差异的第三个数值存在

(二)质量性状资料 质量性状(qualitative trait)指能观察而不能量测的状即 属性性状,如花药、子粒、颖壳等器官的颜色、芒的有 无、绒毛的有无等。要从这类性状获得数量资料,可采 用下列两种方法: 1.统计次数法于一定总体或样本内,统计其具有某个性 状的个体数目及具有不同性状的个体数目,按类别计其 次数或相对次数。 2.给分法给予每类性状以相对数量的方法
(二) 质量性状资料 质量性状( qualitative trait )指能观察而不能量测的状即 属性性状,如花药、子粒、颖壳等器官的颜色、芒的有 无、绒毛的有无等。要从这类性状获得数量资料,可采 用下列两种方法: 1. 统计次数法 于一定总体或样本内,统计其具有某个性 状的个体数目及具有不同性状的个体数目,按类别计其 次数或相对次数。 2. 给分法 给予每类性状以相对数量的方法

二、次数分布表 (一)间断性变数资料的整理 (二)连续性变数资料的整理 (三)属性变数资料的整理
二、次数分布表 (一) 间断性变数资料的整理 (二) 连续性变数资料的整理 (三) 属性变数资料的整理

(一)间断性变数资料的整理 现以某小麦品种的每穗小穗数为例,随机采取 100个麦穗,计数每穗小穗数,未加整理的资料列 成表3.1
(一) 间断性变数资料的整理 现以某小麦品种的每穗小穗数为例,随机采取 100个麦穗,计数每穗小穗数,未加整理的资料列 成表3.1
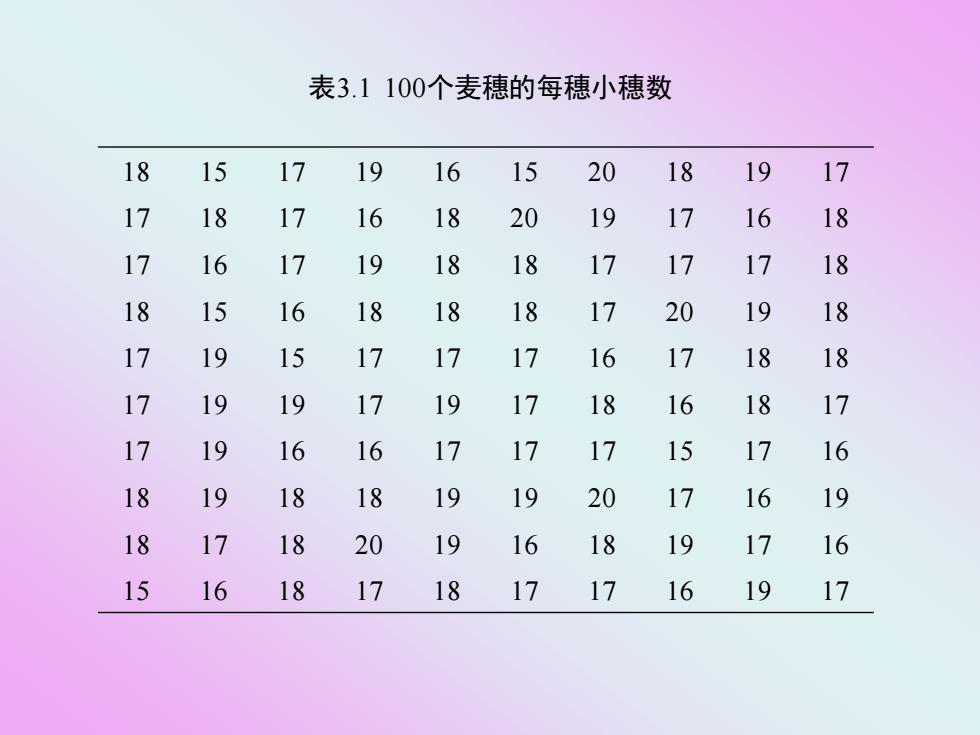
表3.1100个麦穗的每穗小穗数 18 15 17 19 16 15 20 18 19 17 17 18 17 16 18 20 19 17 16 18 17 16 17 19 18 18 17 17 17 18 18 15 18 18 18 19 18 17 19 17 6 18 18 17 19 19 6 18 17 17 19 16 16 17 17 17 15 17 16 18 19 18 18 19 19 20 17 16 19 18 17 18 20 19 16 18 19 17 16 15 16 18 17 18 17 17 16 19 17
表3.1 100个麦穗的每穗小穗数 18 15 17 19 16 15 20 18 19 17 17 18 17 16 18 20 19 17 16 18 17 16 17 19 18 18 17 17 17 18 18 15 16 18 18 18 17 20 19 18 17 19 15 17 17 17 16 17 18 18 17 19 19 17 19 17 18 16 18 17 17 19 16 16 17 17 17 15 17 16 18 19 18 18 19 19 20 17 16 19 18 17 18 20 19 16 18 19 17 16 15 16 18 17 18 17 17 16 19 17