
第十一章 曲线回归 >第一节曲线的类型与特点 >第二节曲线方程的配置 >第三节多项式回归
第十一章 曲线回归 ➢ 第一节 曲线的类型与特点 ➢ 第二节 曲线方程的配置 ➢ 第三节 多项式回归

■曲线回归(curvilinear regression)或非线性 回归(non-linear regression):两个变数间 呈现曲线关系的回归。 ■曲线回归分析或非线性回归分析:以最小二 乘法分析曲线关系资料在数量变化上的特征 和规律的方法
◼ 曲线回归(curvilinear regression)或非线性 回归(non-linear regression):两个变数间 呈现曲线关系的回归。 ◼ 曲线回归分析或非线性回归分析:以最小二 乘法分析曲线关系资料在数量变化上的特征 和规律的方法

■曲线回归分析方法的主要内容有: ·①确定两个变数间数量变化的某种特定的规则或规 律; ·②估计表示该种曲线关系特点的一些重要参数,如 回归参数、极大值、极小值和近值等; ·③为生产预测或试验控制进行内插,或在论据充足 时作出理论上的外推
◼ 曲线回归分析方法的主要内容有: ◼ ① 确定两个变数间数量变化的某种特定的规则或规 律; ◼ ② 估计表示该种曲线关系特点的一些重要参数,如 回归参数、极大值、极小值和渐近值等; ◼ ③ 为生产预测或试验控制进行内插,或在论据充足 时作出理论上的外推

第一节曲线的类型与特点 ■一、指数函数曲线 ■二、对数函数曲线 ■三、幂函数曲线 ■四、双曲函数曲线 ■五、S型曲线
第一节 曲线的类型与特点 ◼ 一、指数函数曲线 ◼ 二、对数函数曲线 ◼ 三、幂函数曲线 ◼ 四、双曲函数曲线 ◼ 五、S型曲线
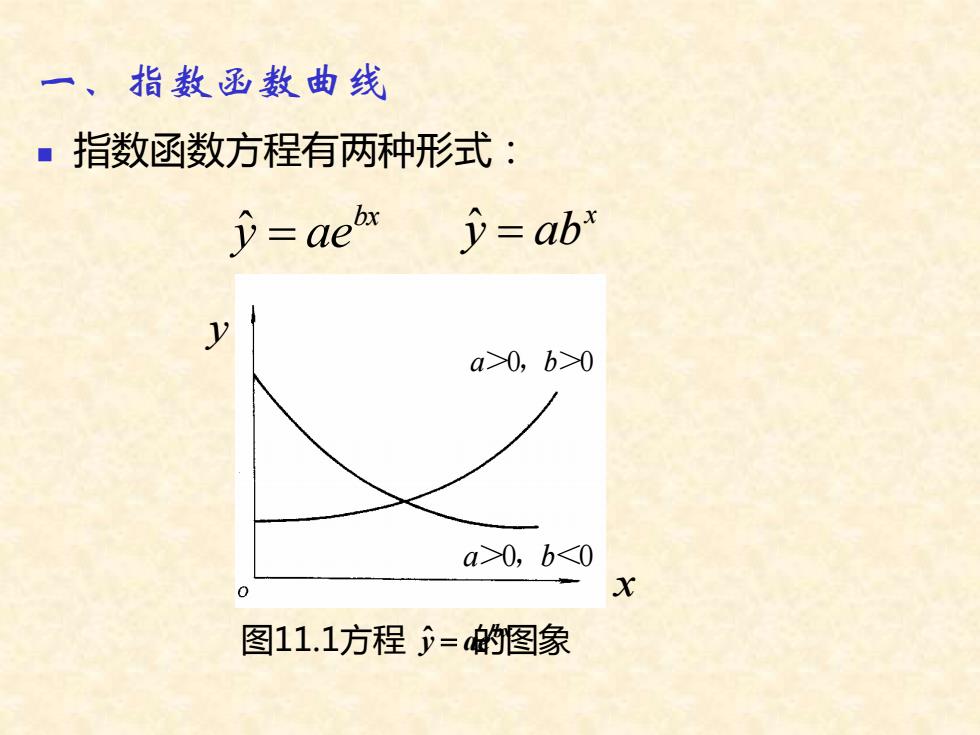
一、指数函数曲线 ■指数函数方程有两种形式: =aeb =ab* y a>0,b>0 a>0,b<0 X 图11.1方程y=的图象
一、指数函数曲线 ◼ 指数函数方程有两种形式: 图11.1方程 的图象 bx y ˆ = ae x y ˆ = ab a>0,b>0 a>0,b<0 bx y ˆ = ae y x
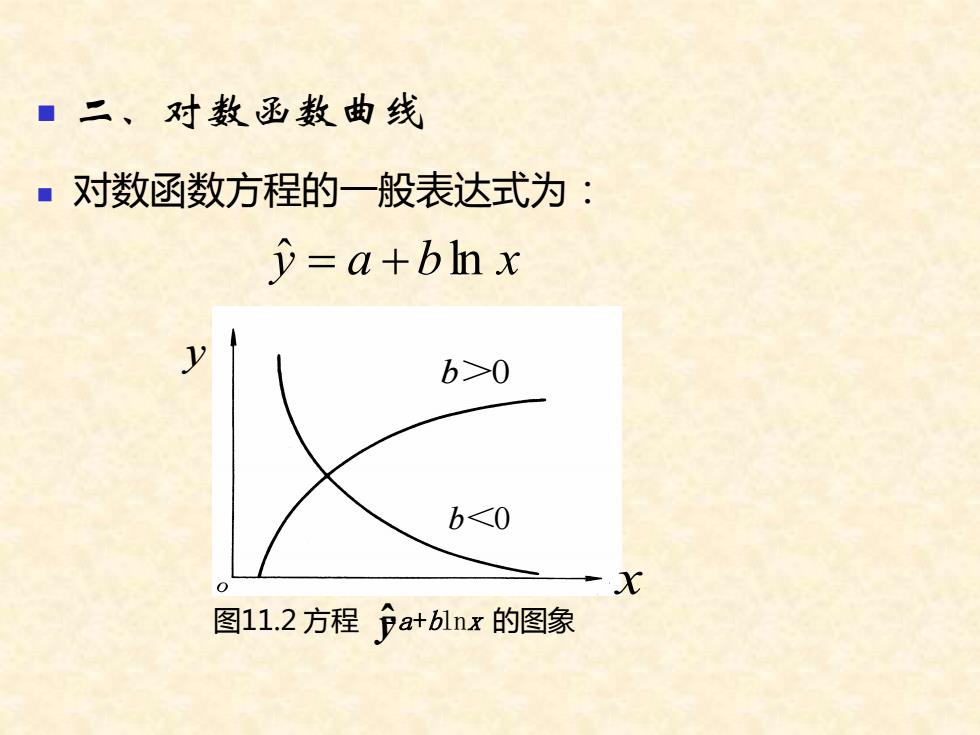
■二、对数函数曲线 ■对数函数方程的一般表达式为: =a+bix b>0 b<0 图11.2方程分a+b1lnx的图象
◼ 二、对数函数曲线 ◼ 对数函数方程的一般表达式为: 图11.2 方程 =a+blnx 的图象 y ˆ = a + bln x b>0 b<0 y ˆ y x
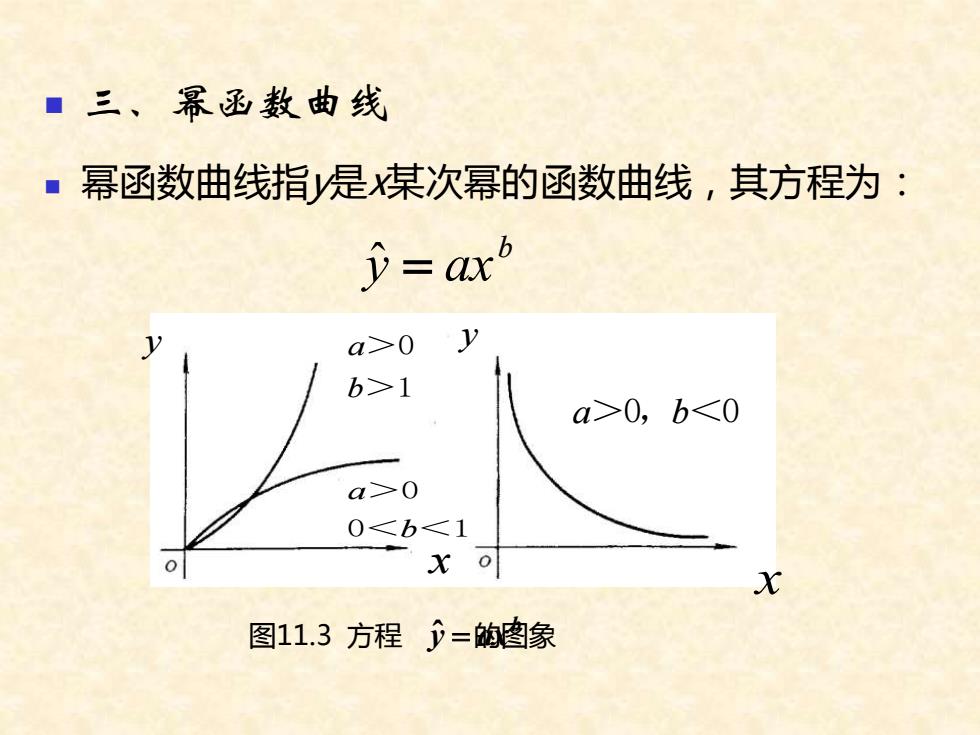
■三、幂函数曲线 ■幂函数曲线指是某次幂的函数曲线,其方程为: =axb a-0 y b>1 a>0,b0 0<b1 x o X 图11.3方程=的图象
◼ 三、幂函数曲线 ◼ 幂函数曲线指y是x某次幂的函数曲线,其方程为: 图11.3 方程 的图象 b y ˆ = ax >1 >0 b a 0< <1 >0 b a a>0,b<0 b y ˆ = ax y y x x

四、双曲函数曲线 ·双曲函数因其属于变形双曲线而得名,其曲线方程 一般有以下3种形式: x a+bx 1 a+bx X a+bx a>0,b0,b>0 x 6 图11.4方程=的图象 a+bx
◼ 四、双曲函数曲线 ◼ 双曲函数因其属于变形双曲线而得名,其曲线方程 一般有以下3种形式: 图11.4 方程 的图象 a bx x y + ˆ = x a bx y + ˆ = a bx y + = 1 ˆ a>0,b>0 b a>0,b<0 1 b a − y y a bx x y + ˆ = x x
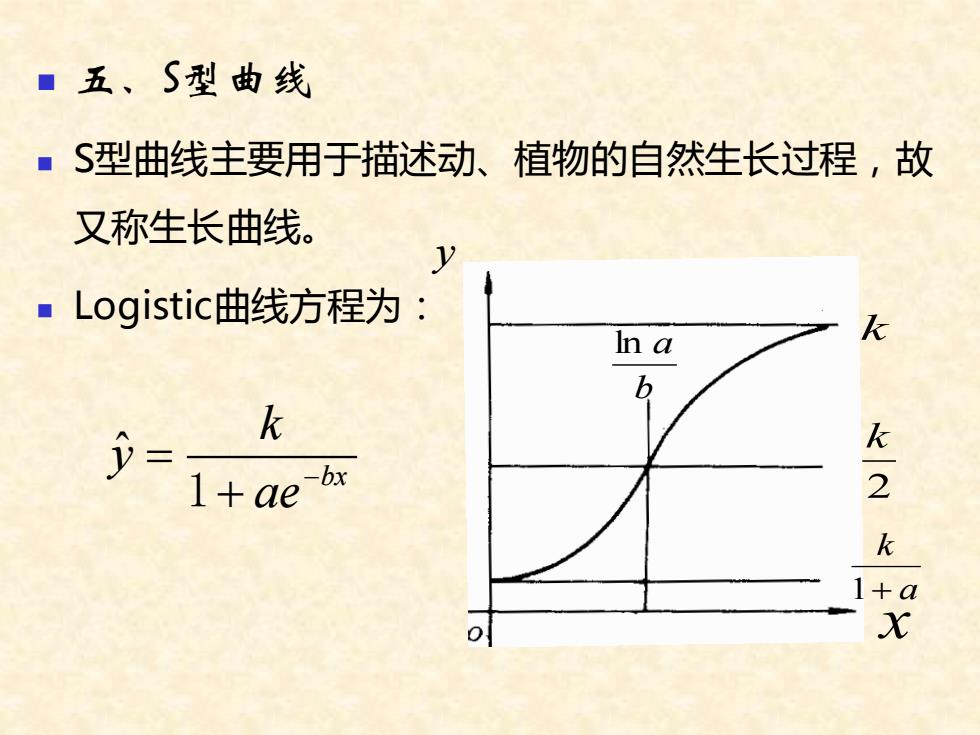
■五、S型曲线 ■S型曲线主要用于描述动、植物的自然生长过程,故 又称生长曲线。 y ■Logisticl曲线方程为: In a k b k 夕= k 1+ae-bx 2 k 1+a X
◼ 五、S型曲线 ◼ S型曲线主要用于描述动、植物的自然生长过程,故 又称生长曲线。 ◼ Logistic曲线方程为: bx ae k y − + = 1 ˆ b ln a k 2 k a k 1+ y x

第二节曲线方程的配置 ■一、曲线回归分析的一般程序 ■二、指数曲线方程少=r的配置 ■三、幂函数曲线方程的配置 ■四、Logistic曲线方程的配置
第二节 曲线方程的配置 ◼ 一、曲线回归分析的一般程序 ◼ 二、指数曲线方程 的配置 ◼ 三、幂函数曲线方程的配置 ◼ 四、Logistic曲线方程的配置 bx y ˆ = ae