
第十四章不完全区组设计和统计分析 ·第一节不完全区组设计的主要类型 ■第二节重复内分组和分组内重复设计的统计分 析 ·第三节简单格子设计的统计分析 ■第四节平衡不完全区组设计的统计分析
第十四章 不完全区组设计和统计分析 ◼ 第一节 不完全区组设计的主要类型 ◼ 第二节 重复内分组和分组内重复设计的统计分 析 ◼ 第三节 简单格子设计的统计分析 ◼ 第四节 平衡不完全区组设计的统计分析

第一节不完全区组设计的主要类型 ■一、田间试验常用设计的归类 ■二、重复内分组和分组内重复设计 ■三、格子设计 ■四、平衡不完全区组设计
第一节 不完全区组设计的主要类型 ◼ 一、田间试验常用设计的归类 ◼ 二、重复内分组和分组内重复设计 ◼ 三、格子设计 ◼ 四、平衡不完全区组设计

一、田间试验常用设计的归类 完全区组(complete block):每一区组包含全套处 理。 ■不完全区组(incomplete block):即一套处理分成 几个区组,或一个区组并不包含全部处理,但同样 要通过区组实施地区控制
一、田间试验常用设计的归类 ◼ 完全区组(complete block):每一区组包含全套处 理。 ◼ 不完全区组(incomplete block):即一套处理分成 几个区组,或一个区组并不包含全部处理,但同样 要通过区组实施地区控制

二、重复内分组和分组内重复设计 "重复内分组设计(block in replication):将供试品种 分为几个组,看作为主区,每个组内包含的各个品 种看作为副区,重复若干次,主副区都按随机区组 布置的设计。 ■例如20个品种,分为4组,每组包含5个品种,若重 复3次,则田间布置可设计如下图:
二、重复内分组和分组内重复设计 ◼ 重复内分组设计(block in replication):将供试品种 分为几个组,看作为主区,每个组内包含的各个品 种看作为副区,重复若干次,主副区都按随机区组 布置的设计。 ◼ 例如20个品种,分为4组,每组包含5个品种,若重 复3次,则田间布置可设计如下图:
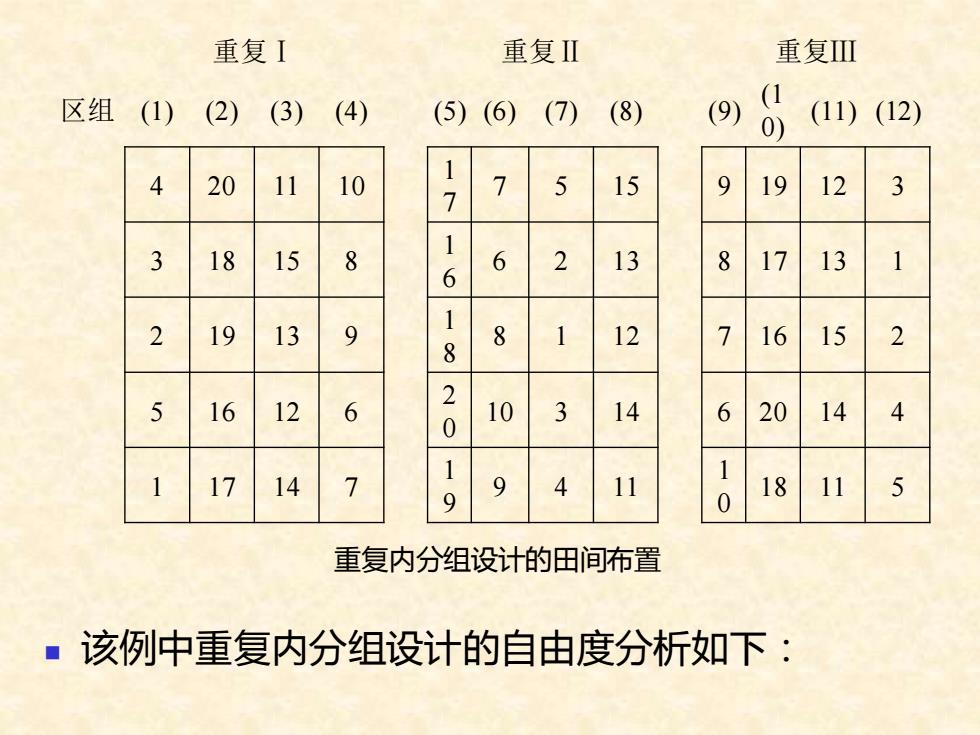
重复I 重复Ⅱ 重复Ⅲ 区组(1)(2)(3) (4) (5)(6)(7) (8) (9) 0 (11)(12) 4 20 11 10 7 7 5 15 9 19 12 3 1 3 18 15 8 6 6 2 13 8 17 13 1 2 19 13 9 1 8 12 16 15 2 8 16 2 5 12 6 0 10 3 14 6 20 14 4 1 17 14 9 9 4 1 0 18 11 5 重复内分组设计的田间布置 ■该例中重复内分组设计的自由度分析如下:
重复内分组设计的田间布置 ◼ 该例中重复内分组设计的自由度分析如下: 重复Ⅰ 重复Ⅱ 重复Ⅲ 区组 (1) (2) (3) (4) (5) (6) (7) (8) (9) (1 0) (11) (12) 4 20 11 10 1 7 7 5 15 9 19 12 3 3 18 15 8 1 6 6 2 13 8 17 13 1 2 19 13 9 1 8 8 1 12 7 16 15 2 5 16 12 6 2 0 10 3 14 6 20 14 4 1 17 14 7 1 9 9 4 11 1 0 18 11 5

■变异来源 DF ■重复 2 ■组间 3 。误差(E) 6 。组内品种间 16 ■误差(E) 32 ■总 59 ■组内品种间比较的误差将为:2Eb/3;
◼ 变 异 来 源 DF ◼ 重 复 2 ◼ 组 间 3 ◼ 误 差 (Ea ) 6 ◼ 组内品种间 16 ◼ 误 差 (Eb ) 32 ◼ 总 59 ◼ 组内品种间比较的误差将为: 2Eb /3 ;

■各组平均数间比较的误差将为:(2/3)(E,/5); ■不同组品种间比较的误差(仿照裂区的情况)将 为:(2/3)(4E6/5+E./5)。 ■由于E,与Eb常取不同数值,E往往大于Eb,例如 E。/E。=3,若如此,则: ■组内品种间比较的误差将为:2E,/3 ■不同组品种间比较的误差将为: ++1c,5
◼ 各组平均数间比较的误差将为: ; ◼ 不同组品种间比较的误差 (仿照裂区的情况)将 为: 。 ◼ 由于Ea与Eb常取不同数值,Ea往往大于Eb,例如 =3,若如此,则: ◼ 组内品种间比较的误差将为: ◼ 不同组品种间比较的误差将为: (2/3)(Ea /5) (2/3)(4Eb /5 + Ea /5) Ea /Eb 2Eb /3 14 /15 5 3 5 4 3 2 5 1 5 4 3 2 Eb Ea Eb Eb = Eb = + +

■两者比值为: (14Eb/15)/(2E6/3)=7/5=1.4 ■即不同组品种间比较的方差将比组内品种间比较的方 差大40%,因而像这种不完全区组设计的方法,并 不能保证任何两个品种间比较具有相近的精确度。 ■分组内重复设计(replication in block):将供试材料 分组后放在连片土地上的几组随机区组试验,通过土 地连片而进行联合分析与比较
◼ 两者比值为: ◼ 即不同组品种间比较的方差将比组内品种间比较的方 差大40%,因而像这种不完全区组设计的方法,并 不能保证任何两个品种间比较具有相近的精确度。 ◼ 分组内重复设计(replication in block):将供试材料 分组后放在连片土地上的几组随机区组试验,通过土 地连片而进行联合分析与比较。 (14 /15)(2 /3)= 7/5 =1.4 Eb Eb
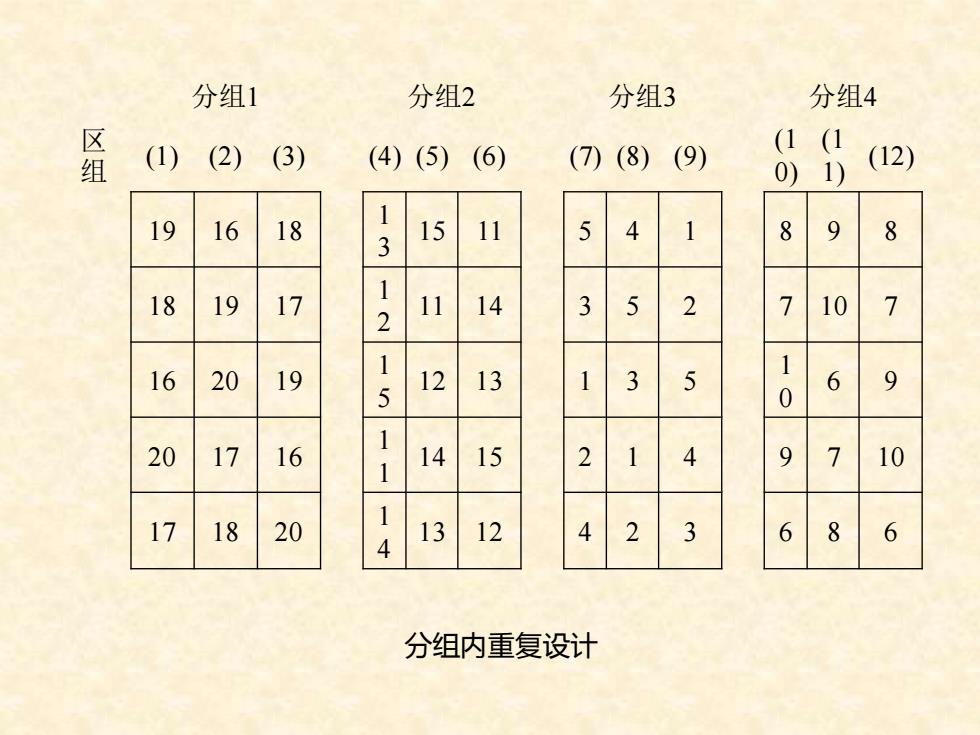
分组1 分组2 分组3 分组4 (1)(2) (3) (4)(5)(6) (7)(8)(9) (1(1 组 0)1) (12) 19 1 16 18 15 11 5 4 8 9 8 3 18 19 17 11 14 3 5 2 7 10 7 2 16 1 20 19 12 13 1 1 3 5 6 9 5 0 1 20 17 16 14 15 2 4 9 7 10 17 18 20 13 12 4 2 3 6 8 6 分组内重复设计
分组内重复设计 分组1 分组2 分组3 分组4 区 组 (1) (2) (3) (4) (5) (6) (7) (8) (9) (1 0) (1 1) (12) 19 16 18 1 3 15 11 5 4 1 8 9 8 18 19 17 1 2 11 14 3 5 2 7 10 7 16 20 19 1 5 12 13 1 3 5 1 0 6 9 20 17 16 1 1 14 15 2 1 4 9 7 10 17 18 20 1 4 13 12 4 2 3 6 8 6

三、格子设计 ■格子设计(lattice design):为了克服重复内分组设 计中组间品种比较和组内品种比较精确度悬殊的问题 对品种分组的方法可考虑从固定的分组改进为不固定 的分组,使一个品种有机会和许多其他品种,甚至其 他各个品种都在同一区组中相遇过
三、 格子设计 ◼ 格子设计(lattice design):为了克服重复内分组设 计中组间品种比较和组内品种比较精确度悬殊的问题, 对品种分组的方法可考虑从固定的分组改进为不固定 的分组,使一个品种有机会和许多其他品种,甚至其 他各个品种都在同一区组中相遇过