
第九章直线回归和相关 ■第一节回归和相关的概念 ■第二节直线回归 ·第三节直线相关 ·第四节直线回归与相关的内在关系 和应用要点 ■第五节协方差分析
第九章 直线回归和相关 ◼ 第一节 回归和相关的概念 ◼ 第二节 直线回归 ◼ 第三节 直线相关 ◼ 第四节 直线回归与相关的内在关系 和应用要点 ◼ 第五节 协方差分析

■引言 这一章研究的对象: ■由一个变数两个或多个变数,因为在实际生 产实践和科学实验中所要研究的变数往往不止一 个,例如: ■研究温度高低和作物发育进度快慢的关系,就有 温度和发育进度两个变数; ■研究每亩穗数、每穗粒数和每亩产量的关系,就 有穗数、粒数和产量三个变数
◼ 引言 这一章研究的对象: ◼ 由一个变数 两个或多个变数,因为在实际生 产实践和科学实验中所要研究的变数往往不止一 个,例如: ◼ 研究温度高低和作物发育进度快慢的关系,就有 温度和发育进度两个变数; ◼ 研究每亩穗数、每穗粒数和每亩产量的关系,就 有穗数、粒数和产量三个变数

第一节回归和相关的概念 ■1.函数关系与统计关系 ■2.自变数与依变数 ■3.回归分析和相关分析 ■4.两个变数资料的散点图
第一节 回归和相关的概念 ◼ 1. 函数关系与统计关系 ◼ 2. 自变数与依变数 ◼ 3. 回归分析和相关分析 ◼ 4. 两个变数资料的散点图
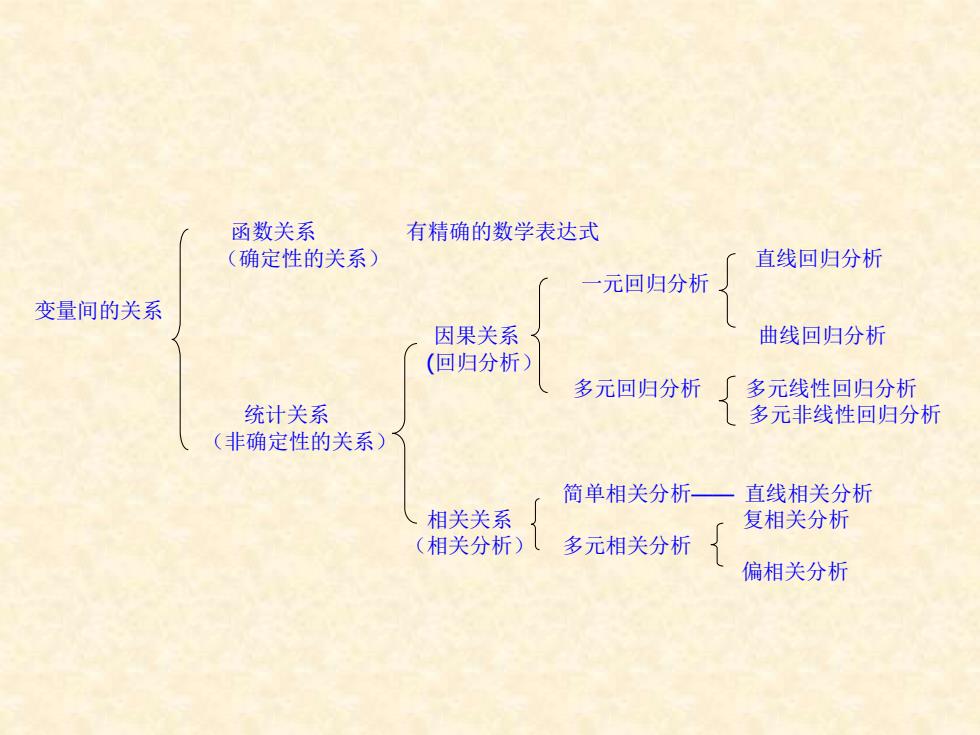
函数关系 有精确的数学表达式 (确定性的关系) 直线回归分析 元回归分析 变量间的关系 因果关系 曲线回归分析 (回归分析) 多元回归分析 多元线性回归分析 统计关系 多元非线性回归分析 (非确定性的关系) 简单相关分析—— 直线相关分析 相关关系 复相关分析 (相关分析)( 多元相关分析 偏相关分析
函数关系 有精确的数学表达式 (确定性的关系) 直线回归分析 一元回归分析 变量间的关系 因果关系 曲线回归分析 (回归分析) 多元回归分析 多元线性回归分析 统计关系 多元非线性回归分析 (非确定性的关系) 简单相关分析—— 直线相关分析 相关关系 复相关分析 (相关分析) 多元相关分析 偏相关分析

·函数关系是一种确定性的关系,例如圆面积 与半径的关系为S=其不包含误差的干 扰。 ■统计关系是一种非确定性的关系。例如,作 物的产量与施肥量的关系,两类变数受误差 的干扰表现为统计关系
◼ 函数关系是一种确定性的关系,例如圆面积 与半径的关系为 。其不包含误差的干 扰。 ◼ 统计关系是一种非确定性的关系。例如,作 物的产量与施肥量的关系,两类变数受误差 的干扰表现为统计关系。 2 S = R

·因果关系:两个变数间的关系若具有原因 和反应(结果)的性质。 相关关系:呈现一种共同变化的特点,则 称这两个变数间存在。 ■回归分析:计算回归方程为基础的统计分 析方法
◼ 因果关系:两个变数间的关系若具有原因 和反应(结果)的性质。 ◼ 相关关系:呈现一种共同变化的特点,则 称这两个变数间存在。 ◼ 回归分析:计算回归方程为基础的统计分 析方法

y=为依X的回归方程(regression equation of YonX)。 ·相关分析:计算相关系数为基础的统计分析方法。 计算表示Y和X相关密切程度的统计数,并测验其 显著性。 ■这个统计数在两个变数为直线相关时称为相关系数 (correlation coefficient),记为r;在多元相关时称 为复相关系数(multiple correlation),记作 R12m;在两个变数曲线相关时称为相关指数 (correlation index),记作R
为Y 依X 的回归方程(regression equation of Y on X )。 ◼ 相关分析:计算相关系数为基础的统计分析方法。 计算表示Y 和X 相关密切程度的统计数,并测验其 显著性。 ◼ 这个统计数在两个变数为直线相关时称为相关系数 (correlation coefficient),记为r;在多元相关时称 为复相关系数(multiple correlation),记作 Ry·12.m ;在两个变数曲线相关时称为相关指数 (correlation index),记作R。 y ˆ = f(x)

■一般规则: 当两个变数中Y含有试验误差而X不含试验误差时 着重进行回归分析;而当Y和X均含有试验误差时 则着重去进行相关分析。 ■4.两个变数资料的散点图 ■对具有统计关系的两个变数的资料进行初步考察 的简便而有效的方法,是将这两个变数的对观察 值(,(,)、(x,y分别以坐标点 的形式标记于同一直角坐标平面上,获得散点图 (scatter diagram)
◼ 一般规则: ◼ 当两个变数中Y 含有试验误差而X 不含试验误差时 着重进行回归分析;而当Y 和X 均含有试验误差时 则着重去进行相关分析。 ◼ 4. 两个变数资料的散点图 ◼ 对具有统计关系的两个变数的资料进行初步考察 的简便而有效的方法,是将这两个变数的n对观察 值(x1,y 1 )、(x2,y 2 )、.、(xn,yn )分别以坐标点 的形式标记于同一直角坐标平面上,获得散点图 (scatter diagram)

■根据散点图可初步判定双变数X和Y间的关系,包 括:①X和Y相关的性质(正或负)和密切程度; ②X和Y的关系是直线型的还是非直线型的; ③是否有一些特殊的点表示着其他因素的干扰等。 ■例如图9.1是水稻方面的3幅散点图,图9.1A是单株 的生物产量(X)和稻谷产量(Y),图9.1B是每平方米 土地上的总颖花数(X)和结实率(Y),图9.1C是最高 叶面积指数(X)和每亩稻谷产量(Y)。从中可以看出: ①图9.1A和9.1B都是直线型的,但方向
◼ 根据散点图可初步判定双变数X 和Y 间的关系,包 括:①X 和Y 相关的性质(正或负)和密切程度; ②X 和Y 的关系是直线型的还是非直线型的; ③是否有一些特殊的点表示着其他因素的干扰等。 ◼ 例如图9.1是水稻方面的3幅散点图,图9.1A是单株 的生物产量(X )和稻谷产量(Y ),图9.1B是每平方米 土地上的总颖花数(X )和结实率(Y ),图9.1C是最高 叶面积指数(X )和每亩稻谷产量(Y )。从中可以看出: ① 图9.1A和9.1B都是直线型的,但方向

相反;前者Y随X的增大而增大,表示两个变数的关 系是正的,后者Y随X的增大而减小,表示关系是负 的。②图9.1A的各个点几乎都落在一直线上,图 9.1B则较为分散;因此,图9.1A中X和Y相关的密 切程度必高于图9.1B。③图9.1C中X和Y的关系是 非直线型的;大约在≤(6一7)时,Y随X的增大而 增大,而当X>(6一7)时,Y随X的增大而减小
相反;前者Y 随X 的增大而增大,表示两个变数的关 系是正的,后者Y 随X 的增大而减小,表示关系是负 的。② 图9.1A的各个点几乎都落在一直线上,图 9.1B则较为分散;因此,图9.1A中X 和Y 相关的密 切程度必高于图9.1B。③ 图9.1C中X 和Y 的关系是 非直线型的;大约在x≤(6—7)时,Y 随X 的增大而 增大,而当x>(6—7)时,Y 随X 的增大而减小