
上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 电路基础 第一 章 基本概念和基本规律 上海交通大学本科学位课程
电路基础 上海交通大学本科学位课程 第一章 基本概念和基本规律

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY §1.4.1电阻元件及其约束方程 基本要求: 掌握电路元件的定义及其电压-电流关系 了解线性与非线性、时变与非时变的概念 了解线性非时变电容电压、电感电流的连续性 2
2 基本要求: 掌握电路元件的定义及其电压-电流关系 了解线性与非线性、时变与非时变的概念 了解线性非时变电容电压、电感电流的连续性 §1.4.1 电阻元件及其约束方程

上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §1.4.1电阻元件及其约束方程 本节所讨论的电路元件都是理想化的二端元件,电路元 件的参数反映了不同基本变量之间的相互关系,而且只 决定于元件的性质,反映电路元件上电压与电流之间关 系的数学表示式,称为元件的约束方程。 一、电阻元件 定义:一个两端元件在任一瞬间 t的电压u和电流之间的关系能由 u-i平面(或i-u平面)上的伏安特 性曲线所决定,称此二端元件为电 阻元件。 3
3 §1.4.1 电阻元件及其约束方程 本节所讨论的电路元件都是理想化的二端元件,电路元 件的参数反映了不同基本变量之间的相互关系,而且只 决定于元件的性质,反映电路元件上电压与电流之间关 系的数学表示式,称为元件的约束方程。 一、电阻元件 定义:一个两端元件在任一瞬间 t 的电压u和电流i之间的关系能由 u-i平面(或i-u平面)上的伏安特 性曲线所决定,称此二端元件为电 阻元件

上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §1.4.1电阻元件及其约束方程 按时间:非时变与时变 电阻元件的分类 按一关系:线性与非线性 1、线性非时变电阻元件 定义:伏安特性曲线是与时间 变化无关的过原点的直线。 u(t)=Ri(t) 解析式 欧姆定律 i(t)=Gu(t) R=1/G 电阻元件的电阻值R(曲线的斜率)是常数,单位欧姆,符 号2,电导G的国际单位是西门子,符号S 4
4 §1.4.1 电阻元件及其约束方程 电阻元件的分类 按时间:非时变与时变 按u-i关系:线性与非线性 1、线性非时变电阻元件 定义:伏安特性曲线是与时间 变化无关的过原点的直线。 解析式 ( ) ( ) ( ) ( ) u t Ri t i t Gu t R G 欧姆定律 =1/ 电阻元件的电阻值R(曲线的斜率)是常数,单位欧姆,符 号Ω,电导G的国际单位是西门子,符号S

上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY S1.4.1电阻元件及其约束方程 线性非时变电阻元件电压-电流关系是线性函数关系 u=f(i) f(ai+Bi2)=af(i)+Bf(i) i=g(u) g(au Buz)=ag(u)+Bg(u2) 齐次性和可加性称线性元件判据 凡线性元件、线性电路,与之相对应的电路变量间 的关系,都是线性函数关系。 伏安曲线对原点为对称,称具有双向性(实际意义: 双向性电阻元件在使用时不必区别二端钮的极性, 可随意接入电路) 5
5 线性非时变电阻元件电压-电流关系是线性函数关系 1 2 1 2 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) u f i f i i f i f i i g u g u u g u g u 齐次性和可加性称线性元件判据 伏安曲线对原点为对称,称具有双向性(实际意义: 双向性电阻元件在使用时不必区别二端钮的极性, 可随意接入电路) 凡线性元件、线性电路,与之相对应的电路变量间 的关系,都是线性函数关系。 §1.4.1 电阻元件及其约束方程
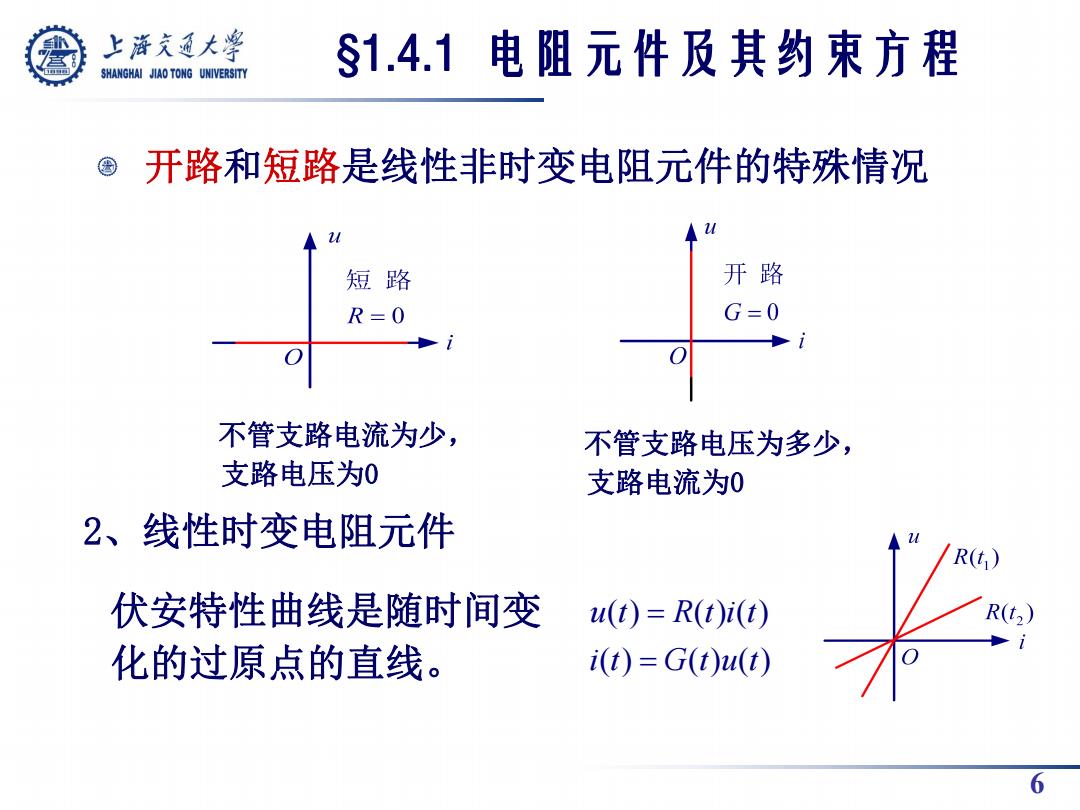
上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §1.4.1电阻元件及其约束方程 开路和短路是线性非时变电阻元件的特殊情况 短路 开路 R=0 G=0 i 不管支路电流为少, 不管支路电压为多少, 支路电压为0 支路电流为0 2、线性时变电阻元件 /R(t) 伏安特性曲线是随时间变 u(t)=R(t)i(t) R(t2 化的过原点的直线。 i(t)=G(t)u(t) 6
6 开路和短路是线性非时变电阻元件的特殊情况 不管支路电流为少, 支路电压为0 不管支路电压为多少, 支路电流为0 2、线性时变电阻元件 伏安特性曲线是随时间变 化的过原点的直线。 ( ) ( ) ( ) ( ) ( ) ( ) u t R t i t i t G t u t §1.4.1 电阻元件及其约束方程

上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §1.4.1电阻元件及其约束方程 ◆R(t) Ra+Rp R+R,cos2πfi /R+Rcos2π R R-R 实验装置电阻器的解析式为 u(t)=(R+Rcos2z.fi)i(t) R>R>0 电压-电流的关系仍然是线性关系即满足齐次性、可加性。 ©每一时刻都有(t),且仍服从欧姆定律。 ©具有双向性。 7
7 实验装置电阻器的解析式为 a b a b u(t) (R R cos2 ft)i(t) R R 0 电压-电流的关系仍然是线性关系 即满足齐次性、可加性。 每一时刻t都有R(t),且仍服从欧姆定律。 具有双向性。 §1.4.1 电阻元件及其约束方程

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY §1.4.1电阻元件及其约束方程 线性非时变电阻元件和线性时变电阻元件的区别 若有正弦信号i=ACos2πft,A,f为常数 则 u=Ri=RAcos2πft u=R(t)i=(R+Rcos2πf)Acos2πft c0s2 对线性非时变电阻而言,输入和输出是同频率的正弦量,对线 性时变电阻而言,其输出中包含有输入信号的频率,还包含有 新的频率(电阻元件时变频率与输入频率的和、差频率),这 种性质在通讯系统中称为“调制”。 8
8 线性非时变电阻元件和线性时变电阻元件的区别 若有正弦信号 对线性非时变电阻而言,输入和输出是同频率的正弦量,对线 性时变电阻而言,其输出中包含有输入信号的频率,还包含有 新的频率(电阻元件时变频率与输入频率的和、差频率),这 种性质在通讯系统中称为“调制” 。 1 i ACos2 f t ,A,f1为常数 则 1 u Ri RAcos2 f t a b 1 b b a 1 1 1 ( ) ( cos2 ) cos2 cos2 cos2 ( ) cos2 ( ) 2 2 u R t i R R ft A f t R A R A R A f t f f t f f t §1.4.1 电阻元件及其约束方程

上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY s1.4.1电阻元件及其约束方程 3、非线性电阻元件 定义:凡不是线性的电阻元件就称为非线性电阻 元件,或伏安特性曲线不是过原点的直线的电阻元件, 称非线性电阻元件。 u(t)f[i(t)] 解析式: i()=g[u()] 9
9 3、非线性电阻元件 定义:凡不是线性的电阻元件就称为非线性电阻 元件,或伏安特性曲线不是过原点的直线的电阻元件, 称非线性电阻元件。 解析式: ( ) ( ) ( ) ( ) u t f i t i t g u t §1.4.1 电阻元件及其约束方程
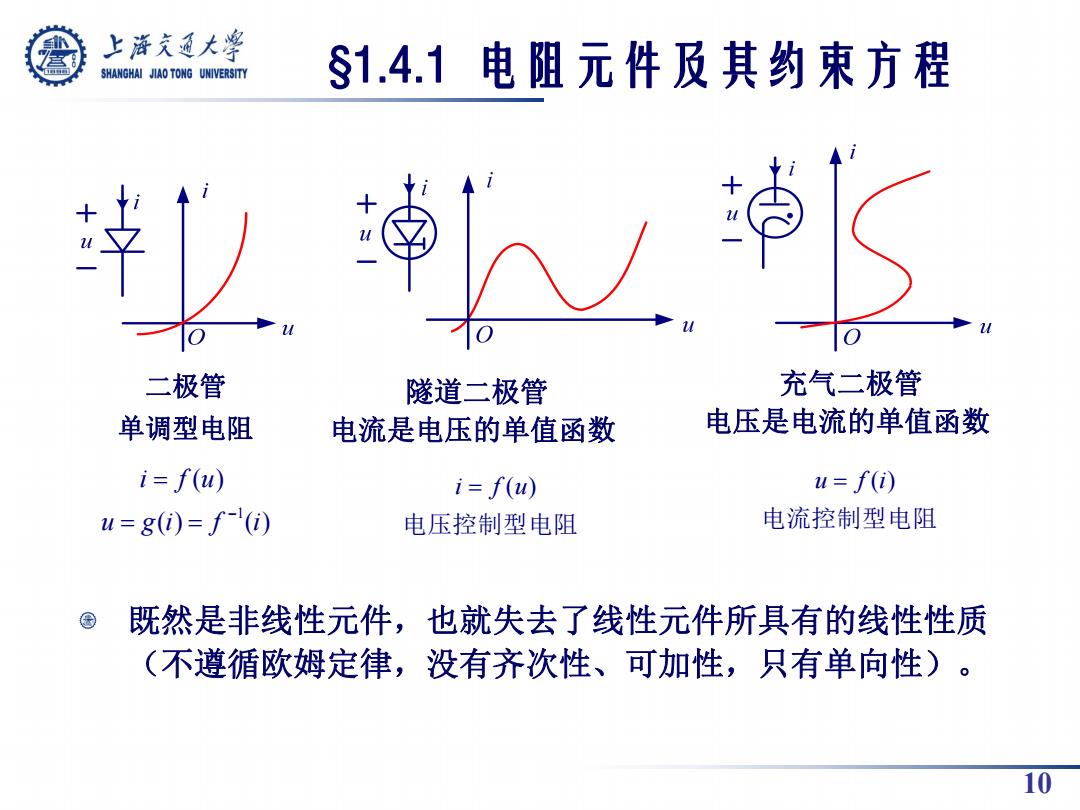
上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §1.4.1电阻元件及其约束方程 二极管 隧道二极管 充气二极管 单调型电阻 电流是电压的单值函数 电压是电流的单值函数 i=f(u) i=f(u) u=f(i) u=g(i)=f-(i) 电压控制型电阻 电流控制型电阻 既然是非线性元件,也就失去了线性元件所具有的线性性质 (不遵循欧姆定律,没有齐次性、可加性,只有单向性)。 10
10 二极管 单调型电阻 隧道二极管 电流是电压的单值函数 充气二极管 电压是电流的单值函数 1 ( ) ( ) ( ) i f u u g i f i i f (u) 电压控制型电阻 u f (i) 电流控制型电阻 既然是非线性元件,也就失去了线性元件所具有的线性性质 (不遵循欧姆定律,没有齐次性、可加性,只有单向性)。 §1.4.1 电阻元件及其约束方程