
上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 电路基础 第三章电路定理 上海交通大学本科学位课程
电路基础 上海交通大学本科学位课程 第三章 电路定理

上游充通大兽 §3.1替代定理 SHANGHAI JIAO TONG UNIVERSITY 替代定理一个有唯一解的电路N,若已知第k 条支路的电压和电流为、k,则不论该支路 是由什么元件组成,总可以用电压为s=4的 电压源或电流为s=k的电流源替代,整个电 路N的工作状态不受影响。 N 2
2 §3.1 替代定理 替代定理 一个有唯一解的电路N,若已知第k 条支路的电压和电流为uk、ik,则不论该支路 是由什么元件组成,总可以用电压为uS= uk的 电压源或电流为iS = ik的电流源替代,整个电 路N的工作状态不受影响

上游充通大学 §3.1替代定理 SHANGHAI JIAO TONG UNIVERSITY 证明 3
3 §3.1 替代定理 证明
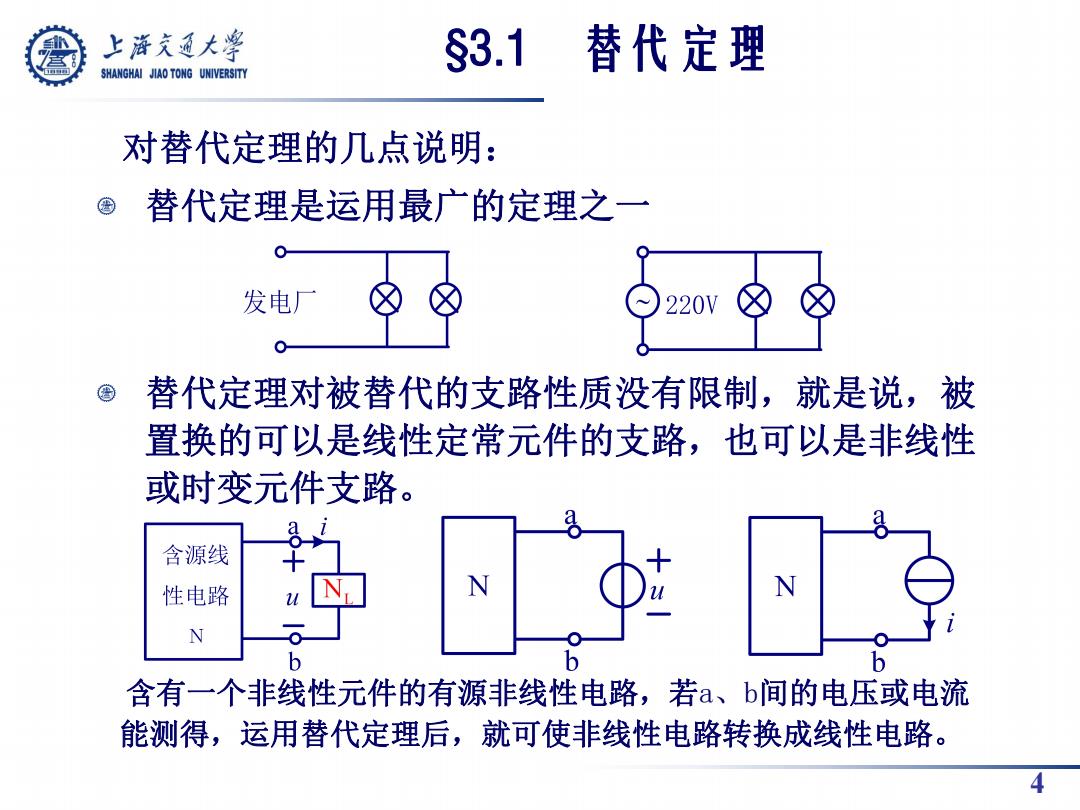
上游文通大学 S3.1 替代定理 SHANGHAI JIAO TONG UNIVERSITY 对替代定理的几点说明: 替代定理是运用最广的定理之一 发电厂 220V 替代定理对被替代的支路性质没有限制,就是说,被 置换的可以是线性定常元件的支路,也可以是非线性 或时变元件支路。 含源线 性电路 N N N b 含有一个非线性元件的有源非线性电路,若a、b间的电压或电流 能测得,运用替代定理后,就可使非线性电路转换成线性电路。 4
4 对替代定理的几点说明: 替代定理是运用最广的定理之一 替代定理对被替代的支路性质没有限制,就是说,被 置换的可以是线性定常元件的支路,也可以是非线性 或时变元件支路。 含有一个非线性元件的有源非线性电路,若a、b间的电压或电流 能测得,运用替代定理后,就可使非线性电路转换成线性电路。 §3.1 替代定理

上游充通大学 3.1替代定理 SHANGHAI JIAO TONG UNIVERSITY 替代后的电路N和N必须有“唯一解” OU U U 当ab左边支路用电流源置换,由于在电流下,隧道二 极管两端的电压不是唯一的,在这种情况下,就不能用 替代定理。若用电流源或电压源去替代隧道二极管,则 是可以的。 定理中所说的被替换支路,一般不应该是受控支路(含 受控源支路)和控制支路(支路电压或支路电流为其它 支路的控制量),也不应该是磁耦合支路。 5
5 替代后的电路Nu和Ni必须有“唯一解” 当ab左边支路用电流源 I置换,由于在电流 I下,隧道二 极管两端的电压不是唯一的,在这种情况下,就不能用 替代定理。若用电流源或电压源去替代隧道二极管,则 是可以的。 定理中所说的被替换支路,一般不应该是受控支路(含 受控源支路)和控制支路(支路电压或支路电流为其它 支路的控制量),也不应该是磁耦合支路。 §3.1 替代定理

上游充通大兽 §3.1替代定理 SHANGHAI JIAO TONG UNIVERSITY 例根据替代定理,电路N被撕裂成如图所示的三个子电路 A u B A B C A B u, C 6
6 例 根据替代定理,电路N被撕裂成如图所示的三个子电路 §3.1 替代定理
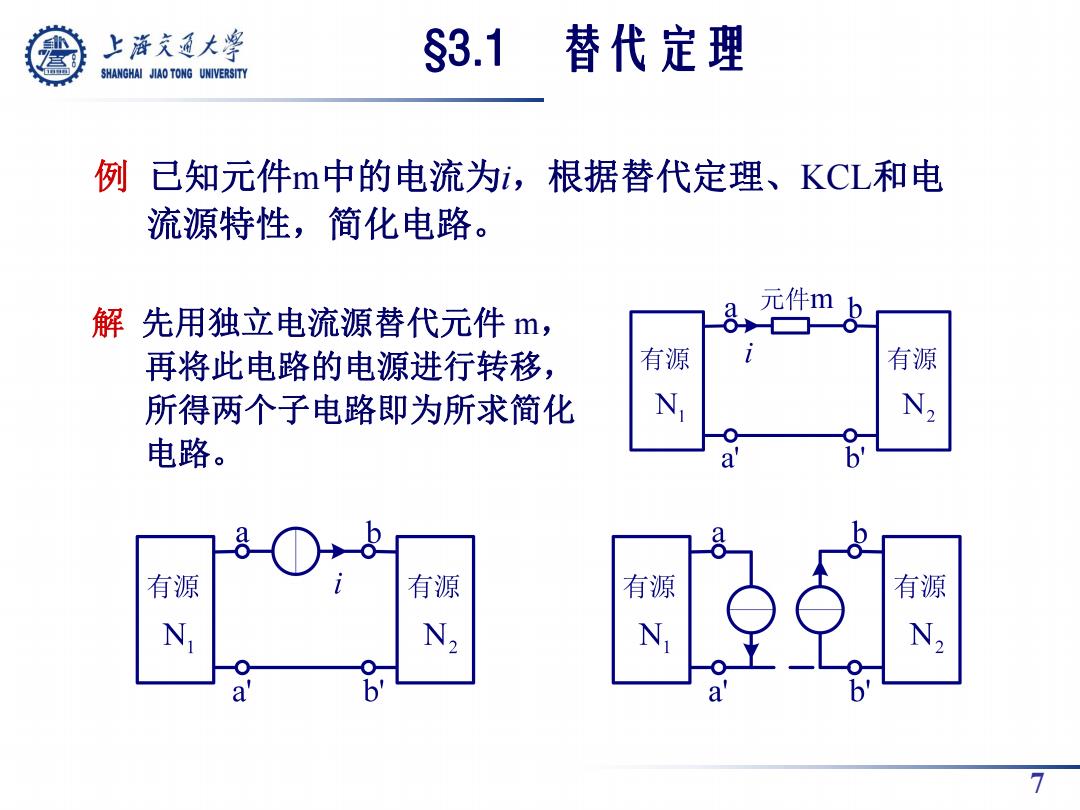
上游充通大兽 §3.1替代定理 SHANGHAI JIAO TONG UNIVERSITY 例已知元件m中的电流为i,根据替代定理、KCL和电 流源特性,简化电路。 解先用独立电流源替代元件m, 8,元件m 再将此电路的电源进行转移, 有源 有源 所得两个子电路即为所求简化 N N2 电路。 a 有源 有源 有源 有源 N N2 N N2 7
7 例 已知元件m中的电流为i,根据替代定理、KCL和电 流源特性,简化电路。 解 先用独立电流源替代元件 m, 再将此电路的电源进行转移, 所得两个子电路即为所求简化 电路。 §3.1 替代定理

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY S3.2 叠加定理 叠加定理 任何由线性电阻元件和独立电源组 成的电路N,其中每一支路的响应(电压或电 流)都等于各个独立源单独作用于电路N时在 该支路中产生的响应的代数和。 设线性电路在n个独立源w(=1,2,.,n)激励下的响应 y w1,w2,.,wn) 就线性电路而言,响应和激励应是线性函数关系 y=f(%,0,…,0)+f(0,w2,…,0)++fn(0,0,…,wn) W,单独作用时的响应 2单独作用时的响应 w,单独作用时的响应 只要是线性电路,叠加定理就成立。 8
8 §3.2 叠加定理 叠加定理 任何由线性电阻元件和独立电源组 成的电路N,其中每一支路的响应(电压或电 流)都等于各个独立源单独作用于电路N时在 该支路中产生的响应的代数和。 设线性电路在 n个独立源 wi(i=1,2, …,n) 激励下的响应 y= f(w1,w2, …, wn) 就线性电路而言,响应和激励应是线性函数关系 1 1 2 2 ( ,0, ,0) (0, , ,0) (0,0, , ) n n w w w y f w f w f w 1单独作用时的响应 2单独作用时的响应 n单独作用时的响应 只要是线性电路,叠加定理就成立

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY §3.2叠加定理 y=f(%,0,…,0)+f5(0,1w2,…,0)+…+(0,0,…,%n) 单独作用时的响应 w,单独作用时的响应 w,单独作用时的响应 上式右端每一项只与一个独立源有关,与其他独立源无 关。无关电源用置零处理。 计算某独立源单独作用于电路所引起的响应时,其余独 立电源都应置零,即电压源用短路代之,电流源用开路 代之,并且要特别注意各分响应的方向。 作为扩充,上式右端的各项可分类成组。每类仅与一组 独立源有关,而与其他组的独立源无关。无关电源用置 零处理。 9
9 上式右端每一项只与一个独立源有关,与其他独立源无 关。无关电源用置零处理。 1 1 2 2 ( ,0, ,0) (0, , ,0) (0,0, , ) n n w w w y f w f w f w 1单独作用时的响应 2单独作用时的响应 n单独作用时的响应 计算某独立源单独作用于电路所引起的响应时,其余独 立电源都应置零,即电压源用短路代之,电流源用开路 代之,并且要特别注意各分响应的方向。 作为扩充,上式右端的各项可分类成组。每类仅与一组 独立源有关,而与其他组的独立源无关。无关电源用置 零处理。 §3.2 叠加定理

上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §3.2叠加定理 例有一线性非时变电阻性电路。 己知U=12V,Is=2A, 测得Uab=0; U=24V,Is=10A, 线性 测得Uab=18V; 电阻电路 试求U=12V,Is=0时的Uab 叠加定理告诉我们,响应UbUs,s)=oUs+1s 根据已有条件有 12a+2B=0 24a+10B=18 解得=3,B=-0.5,∴.Uab=-0.5×12+3×0=-6V 10
10 §3.2 叠加定理 例 有一线性非时变电阻性电路。 已知US=12V,IS=2A, 测得Uab=0; US=24V,IS=10A, 测得Uab=18V; 试求US=12V,IS=0时的Uab。 叠加定理告诉我们,响应Uab= f(US,IS ) = US+IS 根据已有条件有 12 2 0 24 10 18 解得 =3, = -0.5, ∴Uab = -0.5×12+3×0 = -6V