
上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 电路基础 第二章电路分析的基本方法 上海交通大学本科学位课程
电路基础 上海交通大学本科学位课程 第二章 电路分析的基本方法
上游充通大兽 §2.14二端口电路的端口特性分析 SHANGHAI JIAO TONG UNIVERSITY “二端口”的串联 Ua= r =RaTa A 哈 u Ub =RbIb u B 口电流不因连接而破坏下 说=地,设=的三I=b “二端口”A和B进行串联 U= t公 u+u =Ra1a+RI=R+RI=RI ∴.R=Ra+Rb 串联“二端口”的R矩阵为各分“二端口”R矩阵之和 2
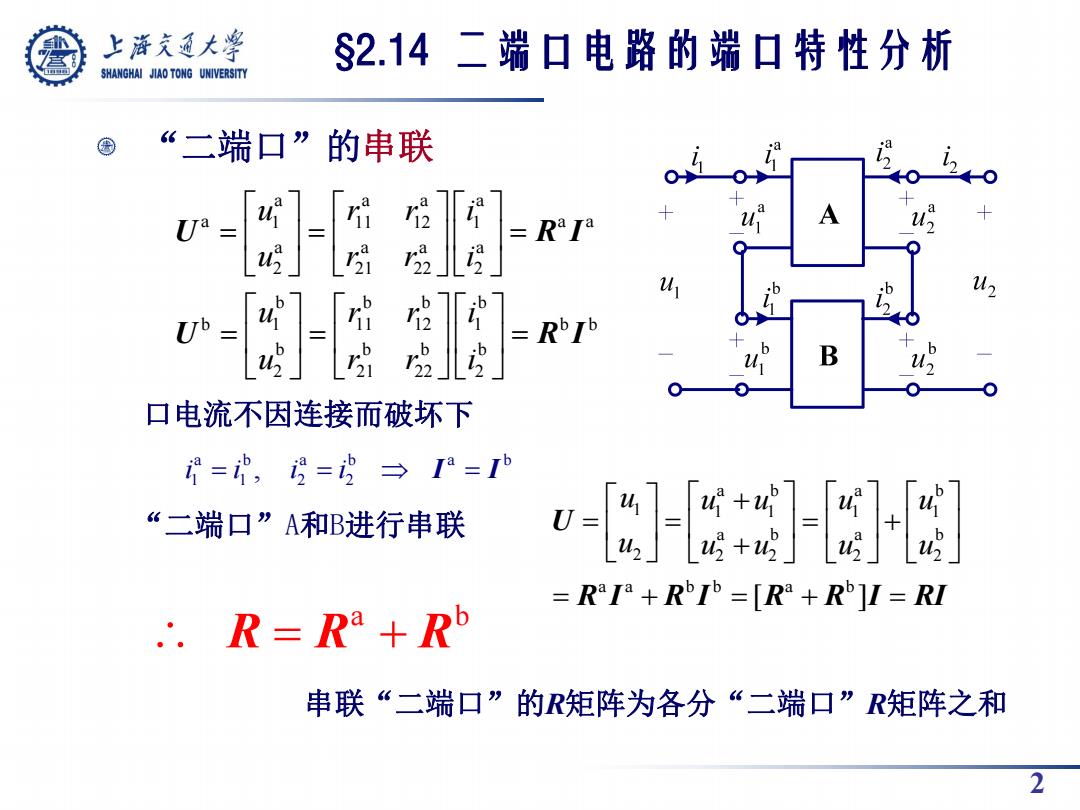
2 “二端口”的串联 口电流不因连接而破坏下 a b a b a b 1 1 2 2 i i , i i I I “二端口”A和B进行串联 串联“二端口”的R矩阵为各分“二端口”R矩阵之和 §2.14 二端口电路的端口特性分析 a a a a a 1 11 12 1 a a a a a a 2 21 22 2 b b b b b 1 11 12 1 b b b b b b 2 21 22 2 u r r i u r r i u r r i u r r i U R I U R I a b a b 1 1 1 1 1 a b a b 2 2 2 2 2 a a b b a b [ ] u u u u u u u u u u U R I R I R R I RI a b R R R

上游充通大兽 §2.14二端口电路的端口特性分析 SHANGHAI JIAO TONG UNIVERSITY 对较复杂“二端口”进行分析时,可将之分解成简单二端口的串 联,使分析简化 ki [ 1 1 当口电流因连接受破坏时,前面的约束不成立 43 P 3
3 对较复杂“二端口”进行分析时,可将之分解成简单二端口的串 联,使分析简化 4 1 1 k 3 3 0 k 2 1 1 1 1 当口电流因连接受破坏时,前面的约束不成立 3 1 1 3 2 1 1 2 4 3 3 4 §2.14 二端口电路的端口特性分析
上游充通大学 §2.14二端口电路的端口特性分析 SHANGHAI JIAO TONG UNIVERSITY 两个“二端口”间的串联连接是否有效,可通过有 效性试验来判定。 当上两图中的电压表的读数都为零时,便可断定把A, B串联起来后不会破坏两端口电流的约束条件。 4
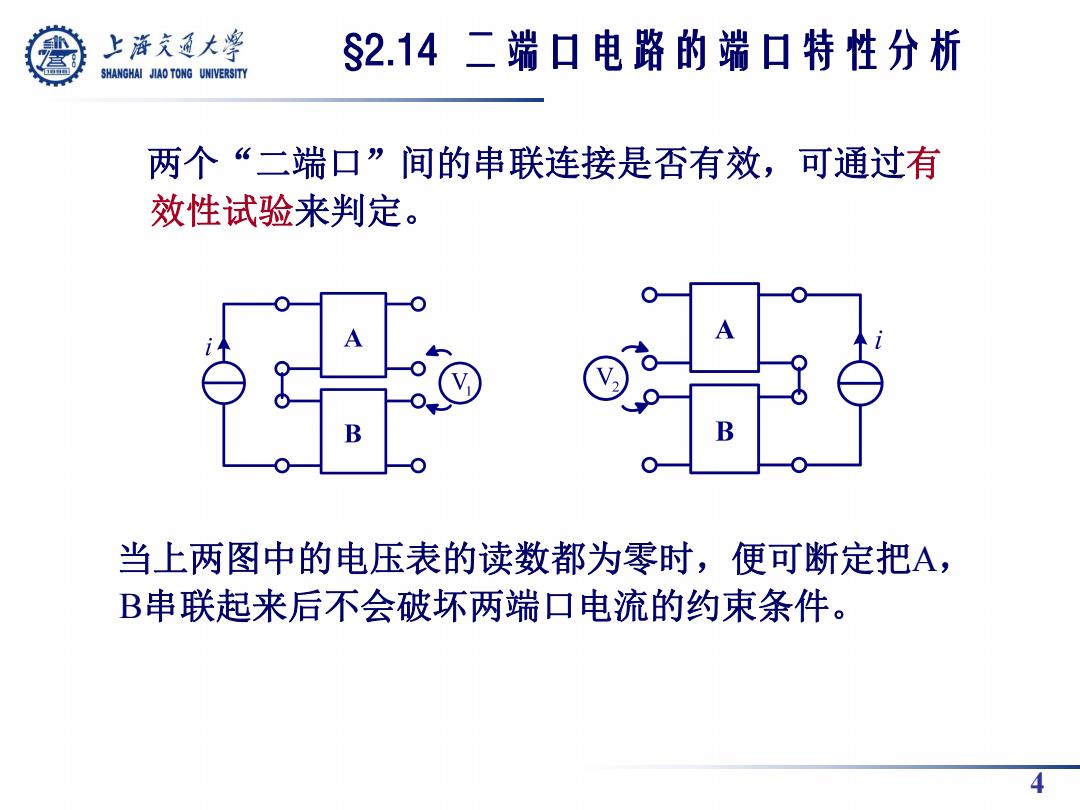
4 两个“二端口”间的串联连接是否有效,可通过有 效性试验来判定。 当上两图中的电压表的读数都为零时,便可断定把A, B串联起来后不会破坏两端口电流的约束条件。 §2.14 二端口电路的端口特性分析
上游充通大兽 §2.14二端口电路的端口特性分析 SHANGHAI JIAO TONG UNIVERSITY “二端口”电路含独立电源时的方程 含独立源的 二端口电路 “二端口电路”含独立电源时的方程可以分两步考虑 不含独立源 含独立源的 二端口电路 二端口电路 i2 r21 22 其中41oc和2oc都是在两端口开路时,由二端口中的独 立源在两端口上产生的开路电压。 5
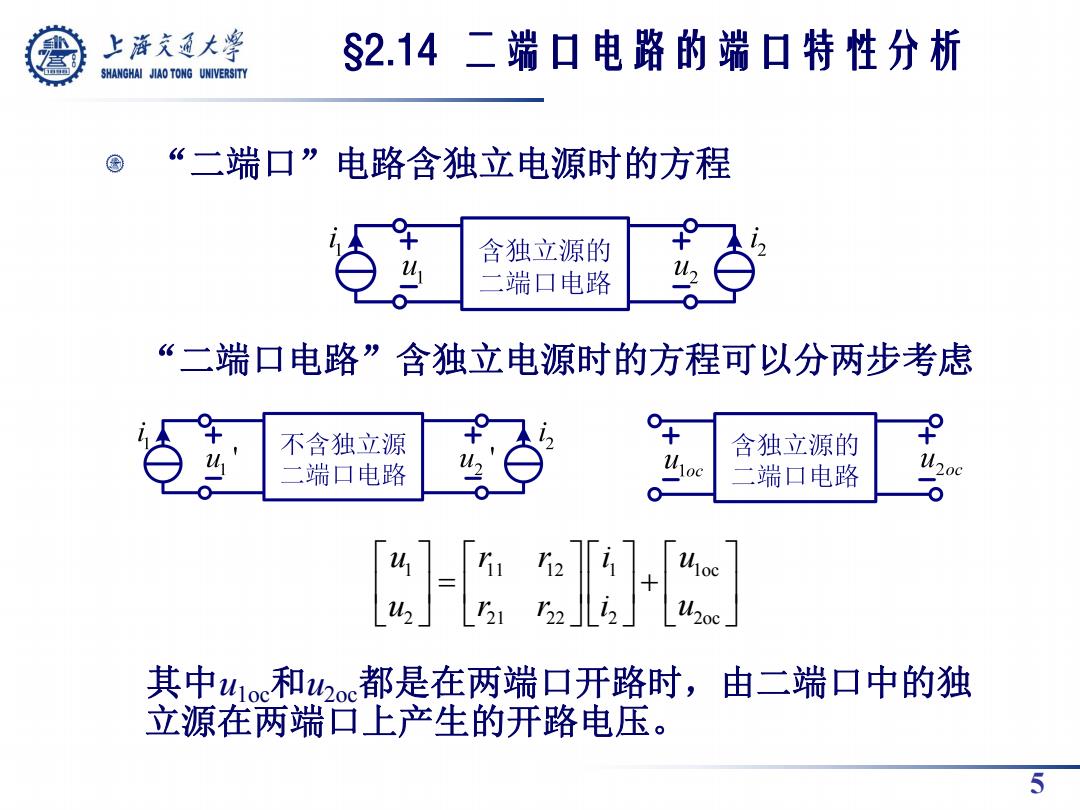
5 “二端口”电路含独立电源时的方程 “二端口电路”含独立电源时的方程可以分两步考虑 其中u1oc和u2oc都是在两端口开路时,由二端口中的独 立源在两端口上产生的开路电压。 §2.14 二端口电路的端口特性分析 1 11 12 1 1oc 2 21 22 2 2oc u r r i u u r r i u
上游充通大兽 §2.14二端口电路的端口特性分析 SHANGHAI JIAO TONG UNIVERSITY 例 R R 求所示二端口电路 的r参数方程。 41 R U, 6 R,0 > 「R+R2 R R R R+R R Uioe =Ri R > uzoc R2i 二端口的r 「R+R 参数方程为: R 6
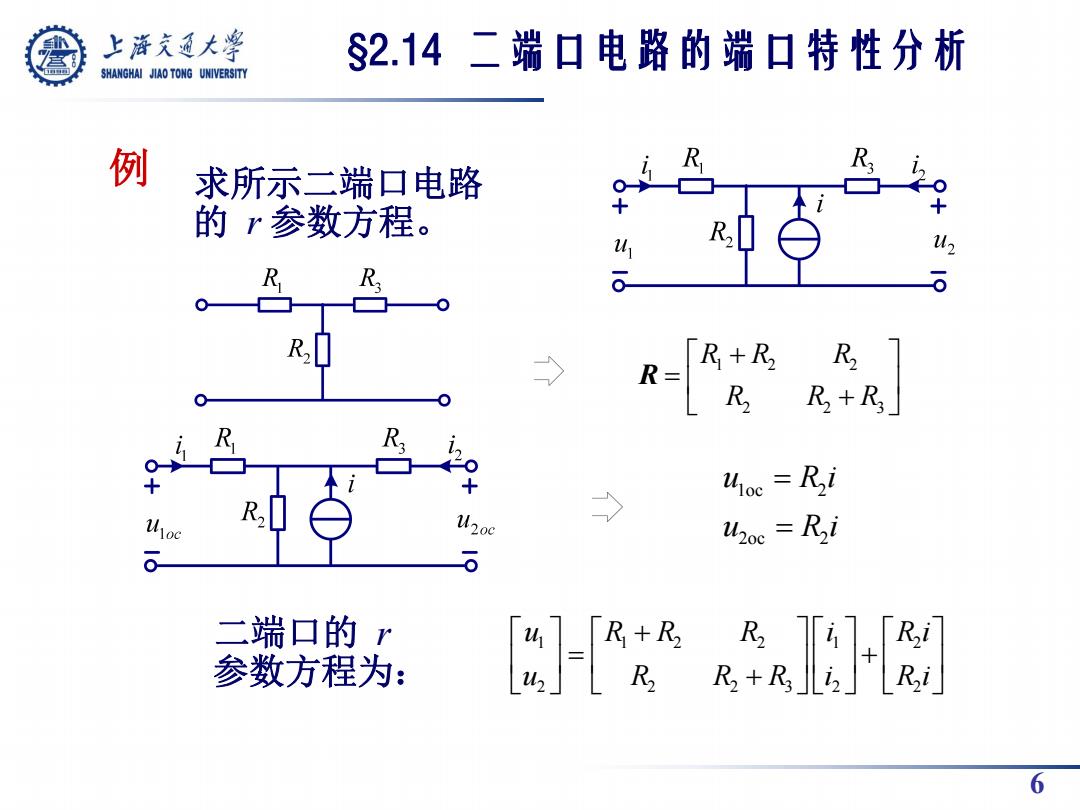
6 求所示二端口电路 的 r 参数方程。 例 二端口的 r 参数方程为: §2.14 二端口电路的端口特性分析 1 2 2 2 2 3 R R R R R R R 1oc 2 2oc 2 u R i u R i 1 1 2 2 1 2 2 2 2 3 2 2 u R R R i R i u R R R i R i
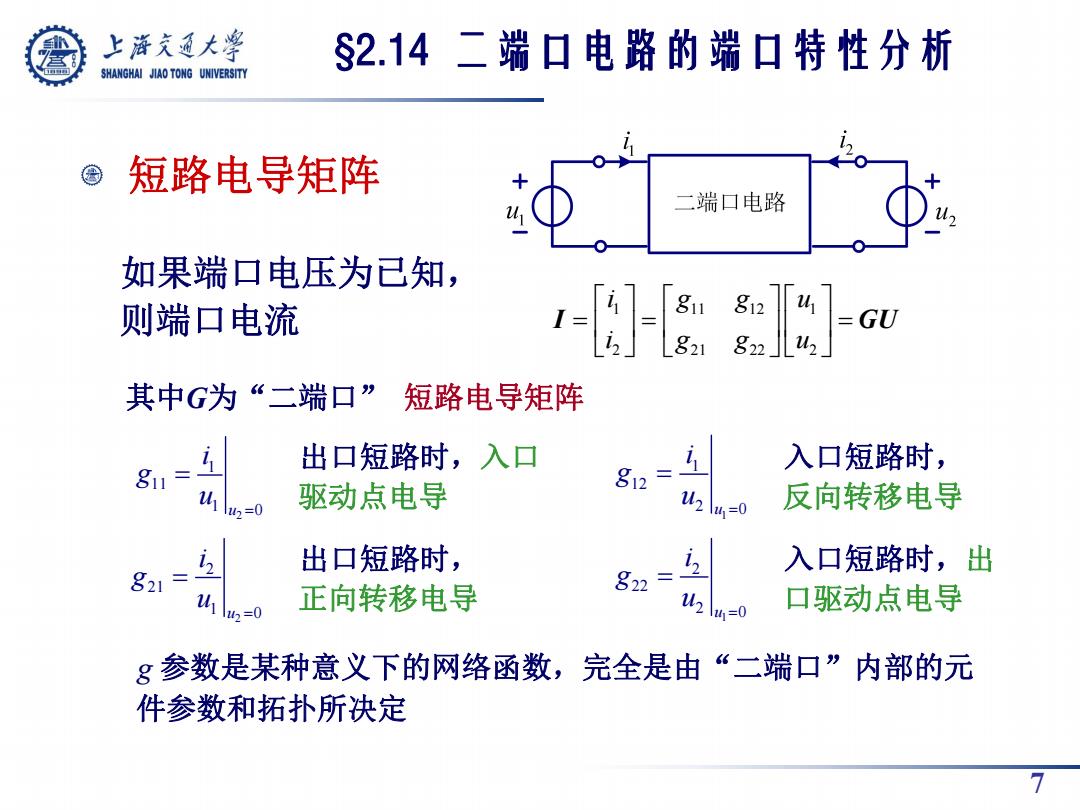
上游充通大兽 §2.14二端口电路的端口特性分析 SHANGHAI JIAO TONG UNIVERSITY 短路电导矩阵 二端口电路 如果端口电压为已知, 则端口电流 I= 811 812 -GU 821 其中G为“二端口”短路电导矩阵 出口短路时,入口 入口短路时, g11= 驱动点电导 g12 U2 \ug=0 反向转移电导 出口短路时, 入口短路时,出 821 正向转移电导 822 u 口驱动点电导 =0 g参数是某种意义下的网络函数,完全是由“二端口”内部的元 件参数和拓扑所决定 7
7 短路电导矩阵 如果端口电压为已知, 则端口电流 其中G为“二端口” 短路电导矩阵 2 1 11 1 u 0 i g u 2 2 21 1 u 0 i g u 1 1 12 2 u 0 i g u 1 2 22 2 u 0 i g u 出口短路时,入口 驱动点电导 入口短路时, 反向转移电导 入口短路时,出 口驱动点电导 出口短路时, 正向转移电导 g 参数是某种意义下的网络函数,完全是由“二端口”内部的元 件参数和拓扑所决定 §2.14 二端口电路的端口特性分析 1 11 12 1 2 21 22 2 i g g u i g g u I GU

上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §2.14二端口电路的端口特性分析 ©用g参数表示的“二端口”等效电路 8121 824 i1=811u1+812u2=81u1+812u1812l1+812l2 =(g11+812)u1-812(u1-2) 2=821u1+8222=821u1-812W1+81241812u2+812l2+8222 =(g21812)u1812(2-u1)+(g12+822)2 2 + -812 822+82 从形等效电路可以看出,如果 821812,则受控源开路,Ⅱ形等 8+82 (821-812)u 效电路成为纯电阻的二端口 8
8 用 g 参数表示的“二端口”等效电路 i1=g11u1+g12u2=g11u1+g12u1-g12u1+g12u2 =(g11+g12)u1-g12(u1-u2) i2=g21u1+g22u2=g21u1-g12u1+g12u1-g12u2+g12u2+g22u2 =(g21-g12)u1-g12(u2-u1)+(g12+g22)u2 从Π形等效电路可以看出,如果 g21=g12,则受控源开路,Π形等 效电路成为纯电阻的二端口 §2.14 二端口电路的端口特性分析 1 11 12 1 2 21 22 2 i g g u i g g u
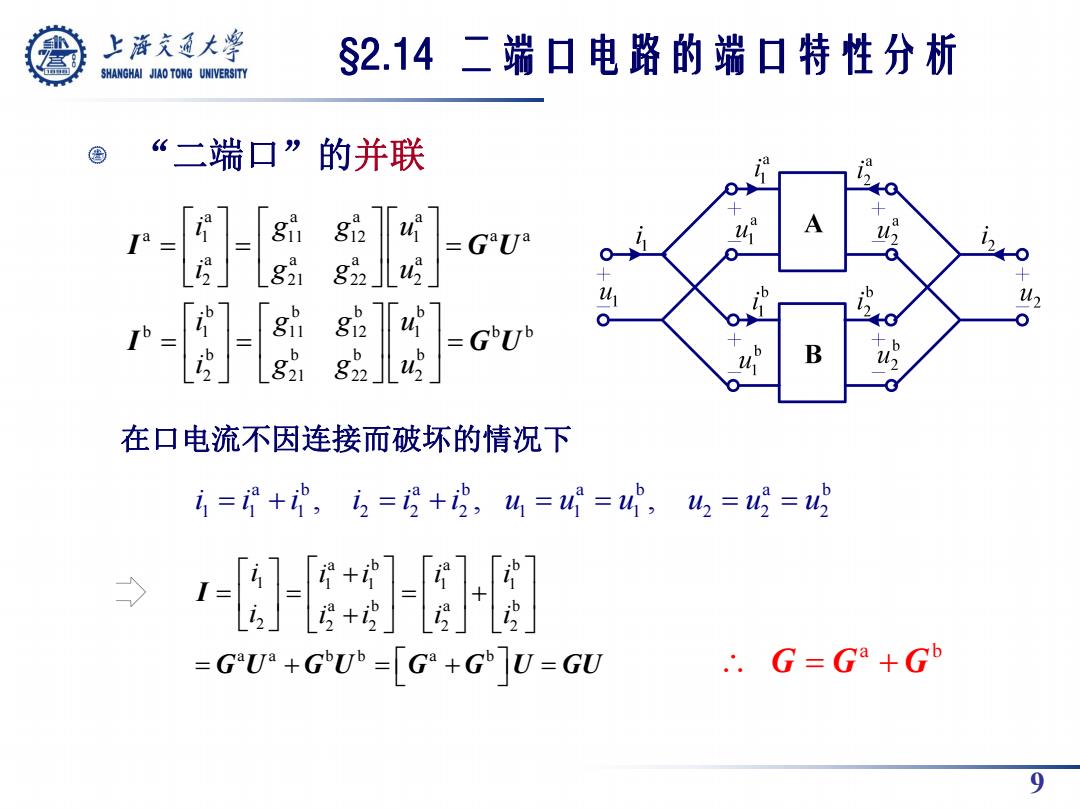
上游充通大兽 §2.14二端口电路的端口特性分析 SHANGHAI JIAO TONG UNIVERSITY “二端口”的并联 a Ia= 」 gi gn u b Ib= 7 812 u B 在口电流不因连接而破坏的情况下 1=+中,=号+,4=4=4, =4 -卧 =GU+GV°=[G+G]0=GU ∴.G=Ga+Gb 9
9 “二端口”的并联 在口电流不因连接而破坏的情况下 a b a b a b a b 1 1 1 2 2 2 1 1 1 2 2 2 i i i , i i i , u u u , u u u §2.14 二端口电路的端口特性分析 a a a a a 1 11 12 1 a a a a a a 2 21 22 2 b b b b b 1 11 12 1 b b b b b b 2 21 22 2 i g g u i g g u i g g u i g g u I G U I G U a b a b 1 1 1 1 1 a b a b 2 2 2 2 2 a a b b a b i i i i i i i i i i I G U G U G G U GU a b G G G
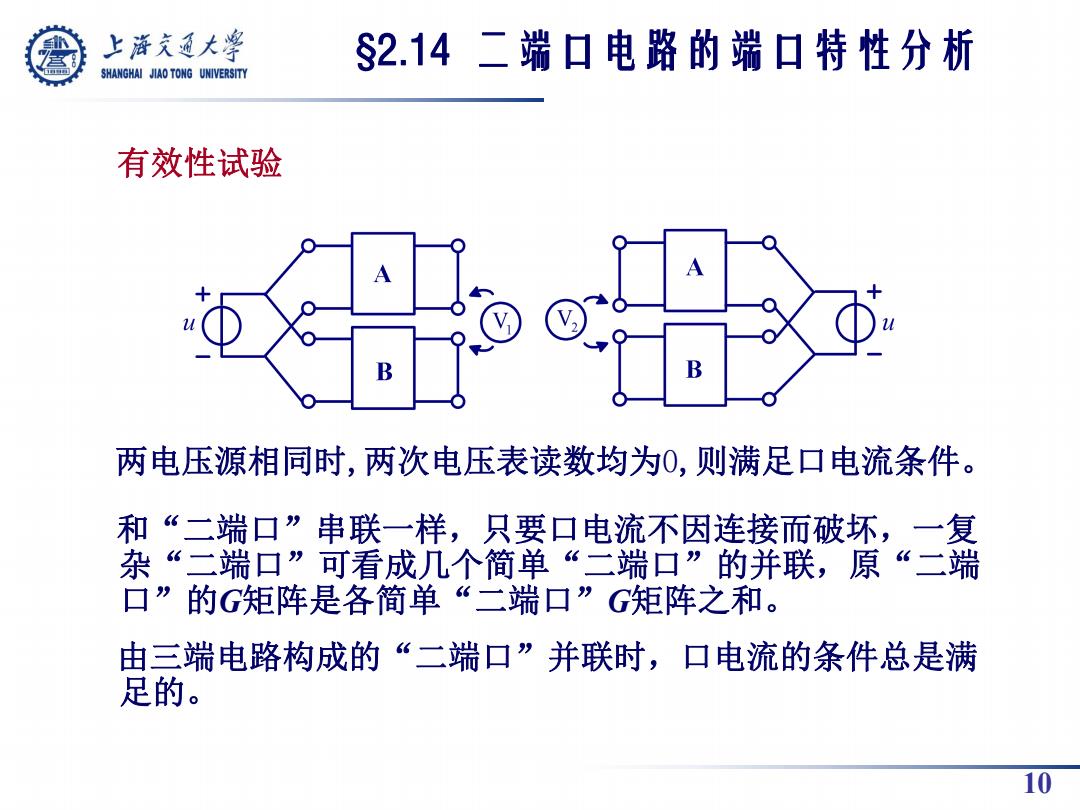
上游充通大学 §2.14二端口电路的端口特性分析 SHANGHAI JIAO TONG UNIVERSITY 有效性试验 B B 两电压源相同时,两次电压表读数均为0,则满足口电流条件。 和“二端口”串联一样,只要口电流不因连接而破坏,一复 杂“二端口”可看成几个简单“二端口”的并联,原“二端 口”的G矩阵是各简单“二端口”G矩阵之和。 由三端电路构成的“二端口”并联时,口电流的条件总是满 足的。 10
10 有效性试验 两电压源相同时,两次电压表读数均为0,则满足口电流条件。 和“二端口”串联一样,只要口电流不因连接而破坏,一复 杂“二端口”可看成几个简单“二端口”的并联,原“二端 口”的G矩阵是各简单“二端口”G矩阵之和。 由三端电路构成的“二端口”并联时,口电流的条件总是满 足的。 §2.14 二端口电路的端口特性分析