
上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 电路基础 第三章 电路定理 上海交通大学本科学位课程 1B三G
电路基础 上海交通大学本科学位课程 第三章 电路定理

上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §3.4互易定理 互易定理1 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮oo'和βB’,如果在端口oo'施加输入 电压,在端口ββ’可得到输出电流,如图所示。反之, 对Bβ’施加输入电压,可在00得到输出电流,如图所 示。 N B N in B' B → 若4B=ua’则。=
§3.4 互易定理 互易定理1 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮 ’和’ ,如果在端口 ’施加输入 电压,在端口’可得到输出电流,如图所示。反之, 对’施加输入电压,可在 ’得到输出电流,如图所 示。 α β sβ sα α β sβ sα ˆ ˆ i i u u i i u u 若 ,则

上游文通大学 互易定理 SHANGHAI JIAO TONG UNIVERSITY S3.4 证明:设电路中有b条支路,连接o0’ 和ββ’的支路电压和电流分别 为 ua ia upy if ie i it ip 根据特勒根定理 u+42+∑4,f=0 i.+p+∑i=0 由于电路N由线性非时变电阻组成,所以 山k=Ri,e=Rie 则有 ui.+g6+∑R,=0 i。+i+∑R,i4.=0 + ui。+42=i。+i6 4=4sa’4g=0,i。=0,ig=弘sB 4。=4p4→ N (一 B 因此, 当弘sB=从su时,ia=3
证明:设电路中有b条支路,连接’和’的支路电压和电流分别 为 α α β β u ,i ,u ,i , α αˆ uˆ ,i , β βˆ uˆ ,i 根据特勒根定理 α α u ˆi β β u ˆi 1 ˆ 0 b k k k u i α α uˆ i β β uˆ i 1 ˆ 0 b k k k u i 由于电路N由线性非时变电阻组成,所以 ˆ ˆ k k k k k k u R i ,u R i 则有 α α u ˆi β β u ˆi 1 ˆ 0 b k k k k R i i α α uˆ i β β uˆ i 1 ˆ 0 b k k k k R i i α α u ˆ i β β u ˆi α α uˆ i β β uˆ i α β Sα α Sβ β sβ sα ˆ ˆ i i u i u i u u Sβ Sα α β u u ˆ 因此,当 时,i i α Sα β α β Sβ u u ,u 0,uˆ 0,uˆ u §3.4 互易定理
上游充通大兽 §3.4 互易定理 SHANGHAI JIAO TONG UNIVERSITY 互易定理2 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮αo'和BB',若在端口oo'施加输入电流, 在端口β邹'可得输出电压,如图所示。反之,对βB施加 输入电压,可在00'得到输出电流,如图所示。 8 B N up N a B' B' 。= →若isp=sa,则da=
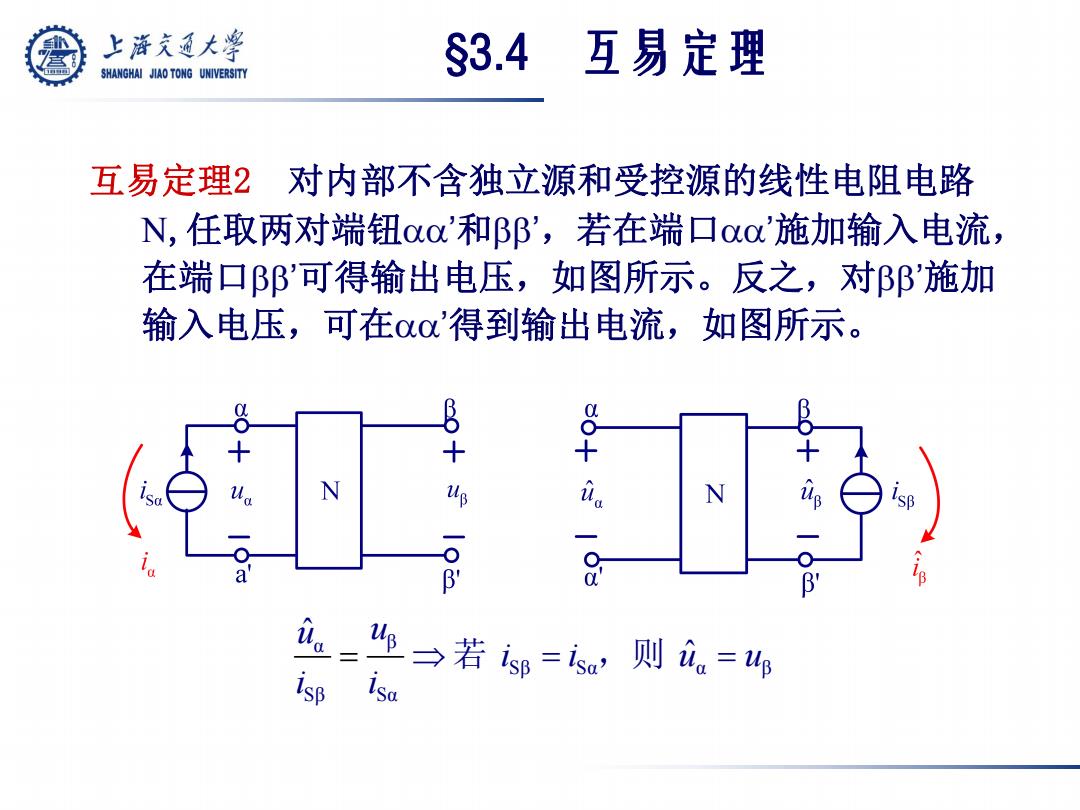
互易定理2 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮 ’和’ ,若在端口 ’施加输入电流, 在端口’可得输出电压,如图所示。反之,对’施加 输入电压,可在 ’得到输出电流,如图所示。 α β Sβ Sα α β Sβ Sα ˆ ˆ u u i i u u i i 若 ,则 §3.4 互易定理
上游充通大兽 互易定理 SHANGHAI JIAO TONG UNIVERSITY 3.4 证明方法同定理1 B 8 + N N β' B' 根据特勒根定理有 uala upl tala igip i。=-ia’6=0,。=0,g=-is .-4sp=-i→ 立= isp isa 因此,当$=s时,元。=4
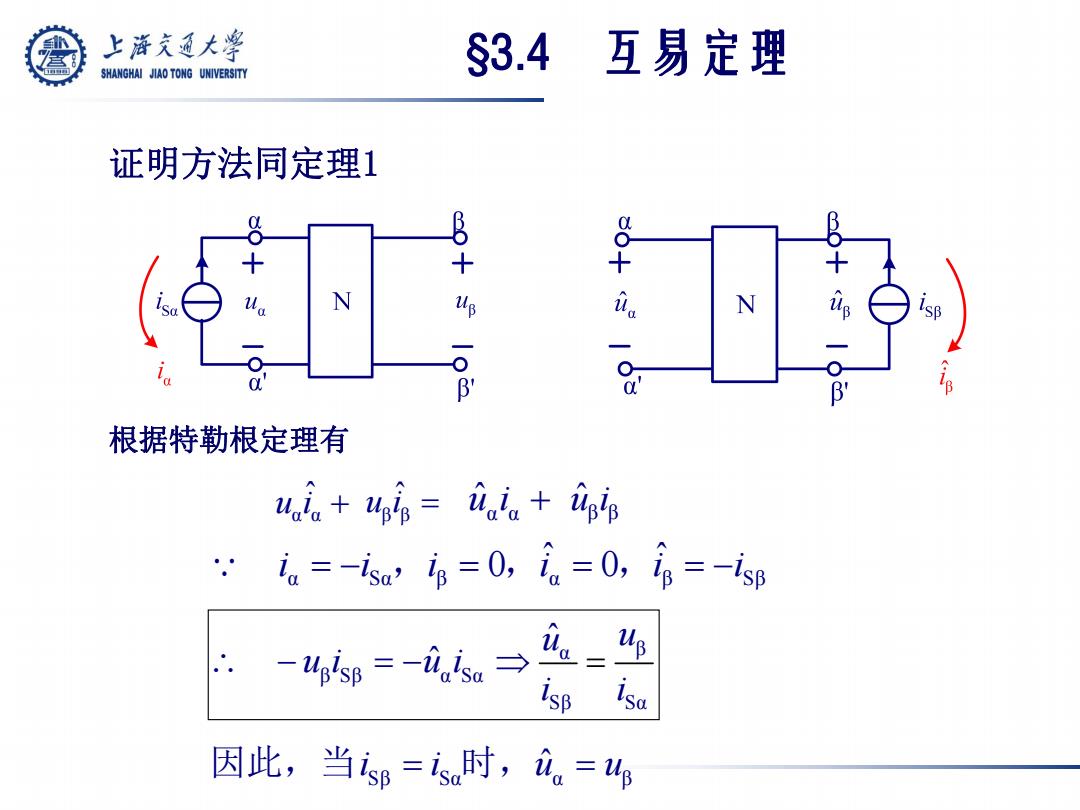
证明方法同定理1 α α u ˆi β β u ˆi α α uˆ i β β uˆ i 根据特勒根定理有 α Sα β α β Sβ i i ,i 0,iˆ 0,iˆ i α β β Sβ α Sα Sβ Sα ˆ ˆ u u u i u i i i Sβ Sα α β 因此,当i i 时,uˆ u §3.4 互易定理
上游文通大学 互易定理 SHANGHAI JIAO TONG UNIVERSITY S3.4 互易定理3 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮oo'和βB',若在端口oo'施加输入电流, 在端口ββ'可得输出电流,如图所示。反之,对Bβ'施加 输入电压,可在00'得到输出电压,如图所示。 + N N B' B i →若4的值=s的值,则i的值=的值
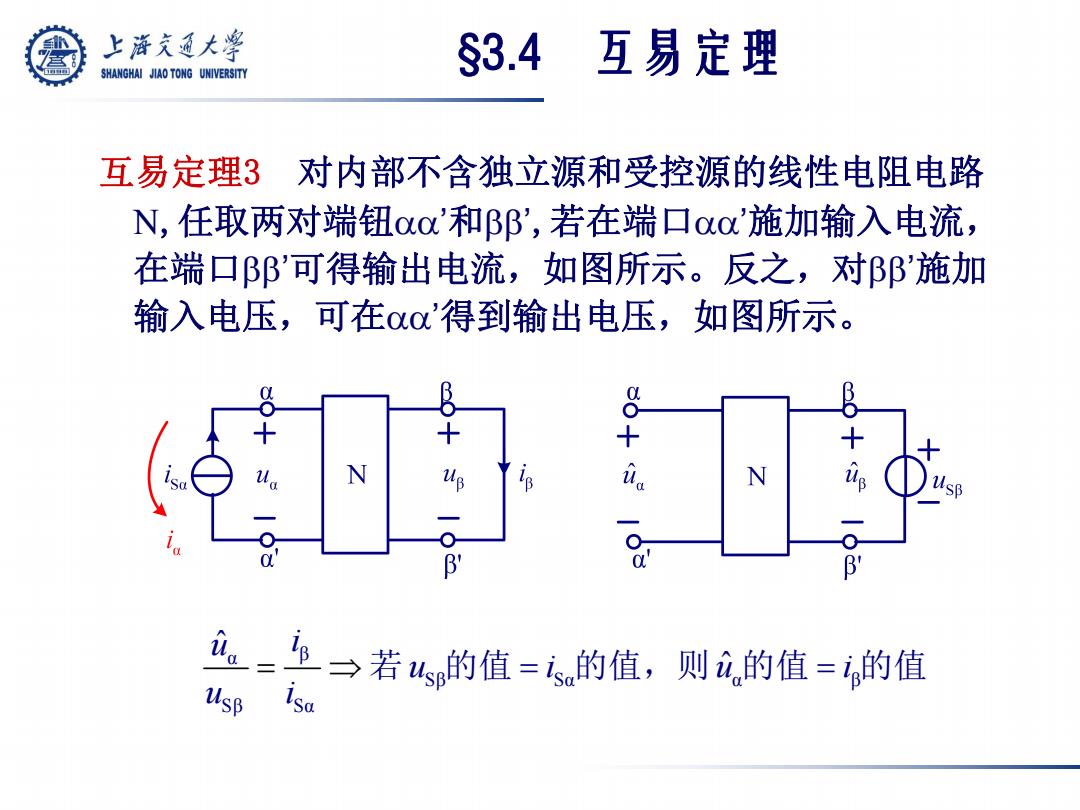
互易定理3 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮 ’和’ ,若在端口 ’施加输入电流, 在端口’可得输出电流,如图所示。反之,对’施加 输入电压,可在 ’得到输出电压,如图所示。 α β Sβ Sα α β Sβ Sα ˆ ˆ u i u i u i u i 若 的值 的值,则 的值 的值 §3.4 互易定理
上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY S3.4 互易定理 证明方法同定理1 B N N 十 SB a' β' g B' 根据特勒根定理有 uala+urlg iala iptp i。=-is4=0,n=0,ip=山sp .0=-5a+弘sB3 i3sa=4sB3→ usB isa 因此,当4s的值=s的值时,i的值=的值
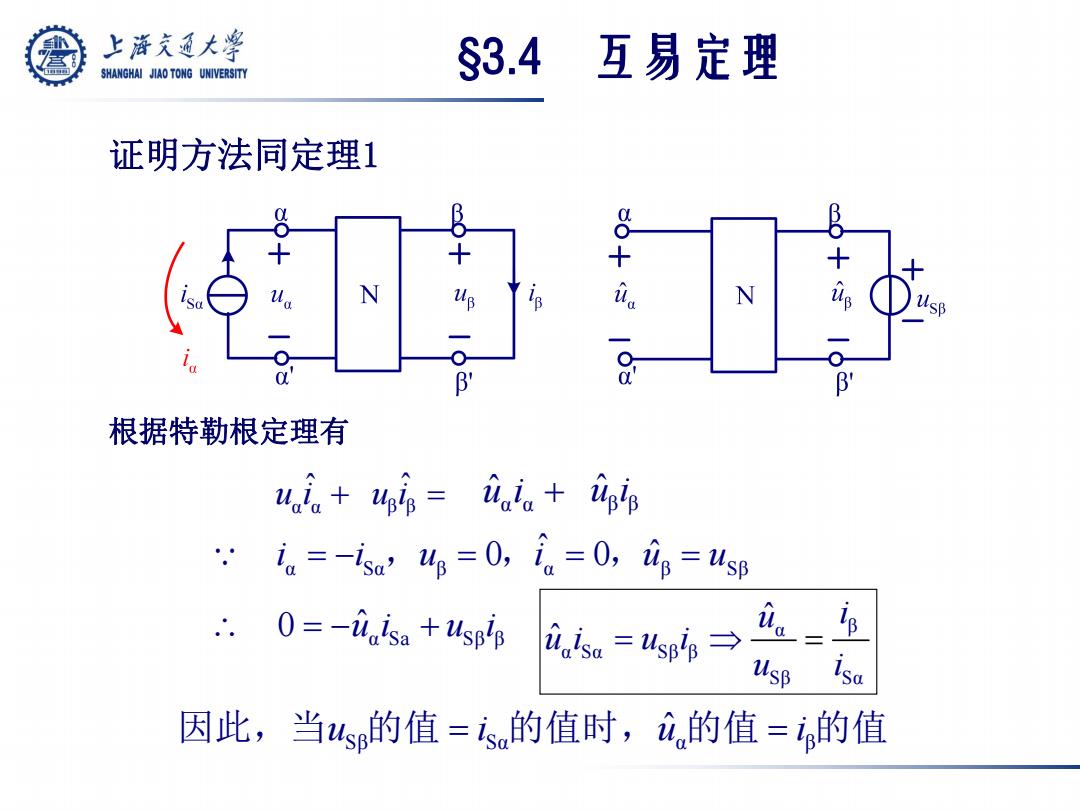
证明方法同定理1 α α u ˆi β β u ˆi α α uˆ i β β uˆ i 根据特勒根定理有 α Sα β α β Sβ ˆ i i ,u 0,i 0,uˆ u α Sa Sβ β 0 uˆ i u i α β α Sα Sβ β Sβ Sα ˆ ˆ u i u i u i u i Sβ Sα α β 因此,当u 的值 i 的值时,uˆ 的值 i 的值 §3.4 互易定理

上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §3.4 互易定理 互易定理的适用范围是比较窄的,它只适用于无源线性非时 变电路。如果电路中有独立源或受控源,非线性元件,时变 元件等,该电路就不能运用互易定理。这是因为线性非时变 电路保证了电路的电阻矩阵和电导矩阵具有对称性,才使互 易性得以成立。 u2≠0 41=0 uw2≠0 =0
§3.4 互易定理 互易定理的适用范围是比较窄的,它只适用于无源线性非时 变电路。如果电路中有独立源或受控源,非线性元件,时变 元件等,该电路就不能运用互易定理。这是因为线性非时变 电路保证了电路的电阻矩阵和电导矩阵具有对称性,才使互 易性得以成立。 u2≠0 u1=0 u2≠0 u1=0

上游充通大学 S3.4互易定理 SHANGHAI JIAO TONG UNIVERSITY 互易定理在应用时要注意,前两种形式中,当激励是 电压,响应为电流;当激励是电流,响应就是电压; 第3种形式,一边激励、响应都是电流,另一边激励、 响应都是电压。从总体上说,不能全是电流或全是电 压。(注意,互易定理中各次观测的响应均为零状态 响应) 应用互易定理时,不仅有量的大小问题,而且还有方 向问题。一般电源的移动方法为:平移法和旋转法。 互易定理用于解平衡电桥电路和对称电路较方便。 互易性与无源性是互不相干的,回转器是无源器件, 但不能互易
互易定理在应用时要注意,前两种形式中,当激励是 电压,响应为电流;当激励是电流,响应就是电压; 第3 种形式,一边激励、响应都是电流,另一边激励、 响应都是电压。从总体上说,不能全是电流或全是电 压。(注意,互易定理中各次观测的响应均为零状态 响应) 应用互易定理时,不仅有量的大小问题,而且还有方 向问题。一般电源的移动方法为:平移法和旋转法。 互易定理用于解平衡电桥电路和对称电路较方便。 互易性与无源性是互不相干的,回转器是无源器件, 但不能互易。 §3.4 互易定理

上游充通大学 3.4互易定理 SHANGHAI JIAO TONG UNIVERSITY 40 8V 022 例 求图示电路中的电流I。 22 12[ 20 解所示为复杂电路,用互易定 理可化简成串并联方法求解 的简单电路。 I1=2A,I2=4/3A,I3=2/3A KCL:=I2-I3=2/3A 此例也说明,同电位不等于 无电流
§3.4 互易定理 例 求图示电路中的电流I。 解 所示为复杂电路,用互易定 理可化简成串并联方法求解 的简单电路。 I1=2A,I2=4/3A,I3=2/3A KCL:I=I2-I3=2/3A 此例也说明,同电位不等于 无电流