
实验四集成霍耳传感器的特性测量与应用 1879年,霍耳(E.H.Hall)在一个用来判断导体中载流子符号的实验中发现了一种电 磁现象,即霍耳效应.后来人们发现半导体、导电流体等也有这种效应,而且半导体的霍 耳效应比金属强很多.基于霍耳效应测定的霍耳系数,可用于确定半导体材料的导电类型、 载流子浓度及迁移率等参数.导电流体中的霍耳效应也是目前正在研究中的“磁流体发电” 的理论基础.近年来,霍耳效应实验不断有新发现.1980年,德国物理学家克利芩(K.vo Klitzing)在低温和强磁场下发现了量子霍耳效应,这是近年来凝聚态物理领域最重要的发 现之一,克利芩也因这一重要发现而获得1985年的诺贝尔物理学奖.目前对量子霍耳效应 仍在进行更深入的实验和理论研究,并己取得了重要应用.例如用于确定电阻的自然基准, 可以极为精确地测定光谱精细结构常数.近三十多年以来,基于霍耳效应用具有高载流子 迁移率的半导体材料制成的霍耳传感器的制造技术和应用得到了全面发展.新的制造技术, 如集成电路技术和分子束外延技术的应用,使得霍耳传感器具有高的可靠性、高的灵敏度 和良好的温度稳定性,而在汽车、电力电子技术、无刷直流电机、电能管理、遥控、遥测、 计算机数据采集以及医疗仪器上形成了广泛的产业性应用. 【实验目的】 1.了解霍耳效应原理和集成霍耳传感器的工作原理: 2.通过测量螺线管励磁电流与集成霍耳传感器输出电压的关系,证明霍耳电势差与磁 感应强度成正比: 3.用通电螺线管中心点处磁感应强度的理论计算值校准集成霍耳传感器的灵敏度: 4.测量螺线管内磁感应强度沿螺线管中轴线的分布,并与相应的理论曲线比较. 【实验原理】 1,霍耳效应 将一导电体(金属或半导体)薄片放在磁场中,并使薄片平面垂直于磁场方向(如图 1所示).当薄片纵向端面有电流I流过时,在与电流I和磁场B垂直的薄片横向端面、b 间就会产生一电势差,这种现象称为霍耳效应(Hall effect),所产生的电势差叫做霍耳电 势差或霍耳电压,用U表示. 霍耳效应是由运动电荷(载流子)在磁场中受到洛伦兹力的作用引起的.洛伦兹力 使载流子发生偏转,在薄片横向端面上聚积电荷形成不断增大的横向电场E组(称霍耳电 +++++++ 十十 ++++ 图1霍耳效应原理 33
33 实验四 集成霍耳传感器的特性测量与应用 1879 年,霍耳(E.H. Hall)在一个用来判断导体中载流子符号的实验中发现了一种电 磁现象,即霍耳效应.后来人们发现半导体、导电流体等也有这种效应,而且半导体的霍 耳效应比金属强很多.基于霍耳效应测定的霍耳系数,可用于确定半导体材料的导电类型、 载流子浓度及迁移率等参数.导电流体中的霍耳效应也是目前正在研究中的“磁流体发电” 的理论基础.近年来,霍耳效应实验不断有新发现.1980 年,德国物理学家克利芩(K.von Klitzing)在低温和强磁场下发现了量子霍耳效应,这是近年来凝聚态物理领域最重要的发 现之一.克利芩也因这一重要发现而获得 1985 年的诺贝尔物理学奖.目前对量子霍耳效应 仍在进行更深入的实验和理论研究,并已取得了重要应用.例如用于确定电阻的自然基准, 可以极为精确地测定光谱精细结构常数.近三十多年以来,基于霍耳效应用具有高载流子 迁移率的半导体材料制成的霍耳传感器的制造技术和应用得到了全面发展.新的制造技术, 如集成电路技术和分子束外延技术的应用,使得霍耳传感器具有高的可靠性、高的灵敏度 和良好的温度稳定性,而在汽车、电力电子技术、无刷直流电机、电能管理、遥控、遥测、 计算机数据采集以及医疗仪器上形成了广泛的产业性应用. 【实验目的】 1.了解霍耳效应原理和集成霍耳传感器的工作原理; 2.通过测量螺线管励磁电流与集成霍耳传感器输出电压的关系,证明霍耳电势差与磁 感应强度成正比; 3.用通电螺线管中心点处磁感应强度的理论计算值校准集成霍耳传感器的灵敏度; 4.测量螺线管内磁感应强度沿螺线管中轴线的分布,并与相应的理论曲线比较. 【实验原理】 1.霍耳效应 将一导电体(金属或半导体)薄片放在磁场中,并使薄片平面垂直于磁场方向(如图 1 所示).当薄片纵向端面有电流 I 流过时,在与电流 I 和磁场 B 垂直的薄片横向端面 a、b 间就会产生一电势差,这种现象称为霍耳效应(Hall effect),所产生的电势差叫做霍耳电 势差或霍耳电压,用 UH表示. 霍耳效应是由运动电荷(载流子)在磁场中受到洛伦兹力的作用引起的.洛伦兹力 fB 使载流子发生偏转,在薄片横向端面上聚积电荷形成不断增大的横向电场 EH(称霍耳电 I I B v - a ---- - ----- + b + ++++ + +++ + + + E fB fE H - I B v + ++++++ + +++ - - ---------- - E f B f E H I a b + 图 1 霍耳效应原理

场),从而使载流子又受到一个与洛伦兹力B反向的电场力E.直到E与相等时,载流 子不再发生偏转,在a、b间形成了一个稳定的霍耳电场.这时,两横向端面a、b间的霍 耳电压就达到一个稳定数值UH.端面a、b间霍耳电压的符号与载流子电荷的正负有关.因 此,通过测量霍耳电压的正负,即可判断半导体材料的导电类型. 实验表明,在外磁场不太强时,霍耳电压U阳与工作电流I和磁感应强度B成正比,与 薄片厚度d成反比,即 UH=RH· B=Ka.I.B (1) d 式中比例系数R:和K:=(R:d)分别称为霍耳系数和霍耳元件的灵敏度.用霍耳效应测 量磁场是在霍耳元件的灵敏度K:和工作电流I己知的条件下,通过测量霍耳电压UH,再 由公式(1)求出磁感应强度B. 2.集成霍耳传感器 SS495A型集成霍耳传感器(线性测量范围0一67mT,灵敏度31.25VT)由霍耳元 件,放大器和薄膜电阻剩余电压补偿器组成(图2).测量时输出信号大,不必考虑剩余电 压的影响.工作电压Us=5V,在磁感应强度为零时,输出电压为U。≈2.5V伏.它的输出 电压U与磁感应强度B的关系如图3所示.该关系可以用下式表示 B=(U-U。)/K (2) 式中U为集成霍耳传感器输出电压,K为该传感器的灵敏度 Vs(+) Vout 4.5v Output (0) 2.5Y Hall 0.5y V-(-) -64 -32 0 32 64 mT 图2SS495A型集成霍耳传感器 图3输出电压与磁感应强度的关系图 3.螺线管内磁场分布 单层通电螺线管内磁感应强度沿螺线管中轴线的分布可由下式计算: (L+2x) (L-2x) =[2p++2+2p+-2严 (3) =C(x)IM 34
34 场),从而使载流子又受到一个与洛伦兹力 fB反向的电场力 fE.直到 fE与 fB相等时,载流 子不再发生偏转,在 a、b 间形成了一个稳定的霍耳电场.这时,两横向端面 a、b 间的霍 耳电压就达到一个稳定数值 UH.端面 a、b 间霍耳电压的符号与载流子电荷的正负有关.因 此,通过测量霍耳电压的正负,即可判断半导体材料的导电类型. 实验表明,在外磁场不太强时,霍耳电压 UH与工作电流 I 和磁感应强度 B 成正比,与 薄片厚度 d 成反比,即 K I B d I B U H RH H = × × × = × (1) 式中比例系数 RH和 KH =(RH /d )分别称为霍耳系数和霍耳元件的灵敏度.用霍耳效应测 量磁场是在霍耳元件的灵敏度 KH和工作电流 I 已知的条件下,通过测量霍耳电压 UH,再 由公式(1)求出磁感应强度 B. 2.集成霍耳传感器 SS495A 型集成霍耳传感器(线性测量范围 0 — 67 mT,灵敏度 31.25 V /T)由霍耳元 件,放大器和薄膜电阻剩余电压补偿器组成(图 2).测量时输出信号大,不必考虑剩余电 压的影响.工作电压 US = 5 V,在磁感应强度为零时,输出电压为 Uo ≈ 2.5 V 伏.它的输出 电压 U 与磁感应强度 B 的关系如图 3 所示.该关系可以用下式表示 B = (U -Uo )/ K (2) 式中 U 为集成霍耳传感器输出电压,K 为该传感器的灵敏度. 3.螺线管内磁场分布 单层通电螺线管内磁感应强度沿螺线管中轴线的分布可由下式计算: [ ] ( ) [ ] ( ) M M C x I D L x L x D L x L x I L N B x ( ) 2 2 ( 2 ) 2 2 ( 2 ) ( ) 1 / 2 2 2 1 / 2 2 2 0 = ú ú û ù ê ê ë é + - - + + + + = m (3) 4.5V 2.5V 0.5V -64 -32 0 32 64 mT Vout > Output(O) Vs(+) V-(-) Hall Sensor CC 图 2 SS495A 型集成霍耳传感器 图 3 输出电压与磁感应强度的关系图
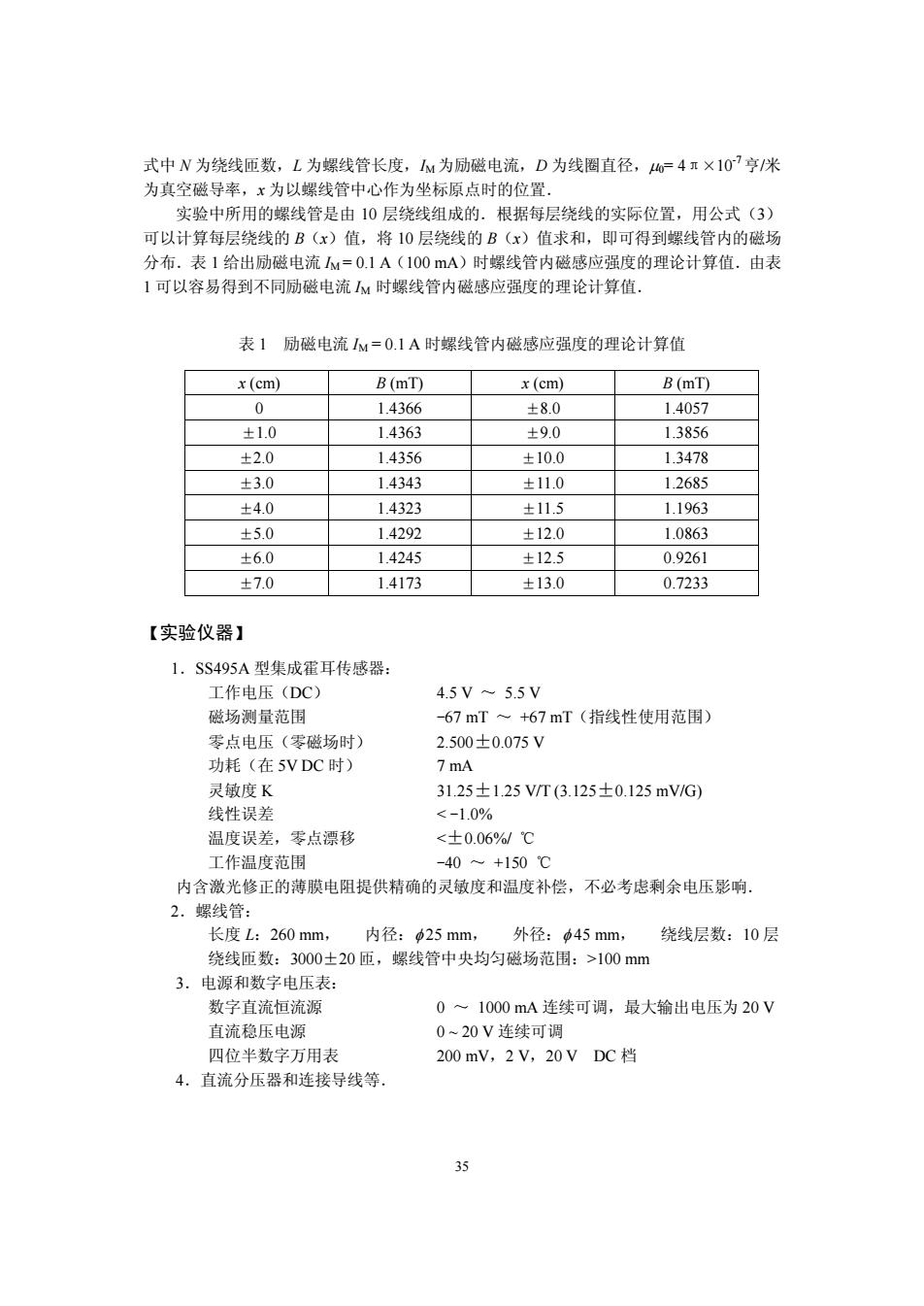
式中N为绕线匝数,L为螺线管长度,M为励磁电流,D为线圈直径,=4π×10?亨/米 为真空磁导率,x为以螺线管中心作为坐标原点时的位置. 实验中所用的螺线管是由10层绕线组成的.根据每层绕线的实际位置,用公式(3) 可以计算每层绕线的B(x)值,将10层绕线的B(x)值求和,即可得到螺线管内的磁场 分布.表1给出励磁电流M=0.1A(100mA)时螺线管内磁感应强度的理论计算值.由表 1可以容易得到不同励磁电流M时螺线管内磁感应强度的理论计算值, 表1励磁电流M=0.1A时螺线管内磁感应强度的理论计算值 x (cm) B(mT) x(cm) B(mT) 0 1.4366 ±8.0 1.4057 ±1.0 1.4363 ±9.0 1.3856 ±2.0 1.4356 ±10.0 1.3478 ±3.0 1.4343 ±11.0 1.2685 ±4.0 1.4323 ±11.5 1.1963 ±5.0 1.4292 ±12.0 1.0863 ±6.0 1.4245 ±12.5 0.9261 ±7.0 1.4173 ±13.0 0.7233 【实验仪器】 1.SS495A型集成霍耳传感器: 工作电压(DC) 4.5V-5.5V 磁场测量范围 -67mT~+67mT(指线性使用范围) 零点电压(零磁场时) 2.500±0.075V 功耗(在5VDC时) 7mA 灵敏度K 31.25±1.25VT(3.125±0.125mV/G) 线性误差 100mm 3.电源和数字电压表: 数字直流恒流源 0~1000mA连续可调,最大输出电压为20V 直流稳压电源 0~20V连续可调 四位半数字万用表 200mV,2V,20VDC档 4.直流分压器和连接导线等 35
35 式中 N 为绕线匝数,L 为螺线管长度,IM为励磁电流,D 为线圈直径,m0= 4π×10-7亨/米 为真空磁导率,x 为以螺线管中心作为坐标原点时的位置. 实验中所用的螺线管是由 10 层绕线组成的.根据每层绕线的实际位置,用公式(3) 可以计算每层绕线的 B(x)值,将 10 层绕线的 B(x)值求和,即可得到螺线管内的磁场 分布.表 1 给出励磁电流 IM = 0.1 A(100 mA)时螺线管内磁感应强度的理论计算值.由表 1 可以容易得到不同励磁电流 IM 时螺线管内磁感应强度的理论计算值. 表 1 励磁电流 IM = 0.1 A 时螺线管内磁感应强度的理论计算值 x (cm) B (mT) x (cm) B (mT) 0 1.4366 ±8.0 1.4057 ±1.0 1.4363 ±9.0 1.3856 ±2.0 1.4356 ±10.0 1.3478 ±3.0 1.4343 ±11.0 1.2685 ±4.0 1.4323 ±11.5 1.1963 ±5.0 1.4292 ±12.0 1.0863 ±6.0 1.4245 ±12.5 0.9261 ±7.0 1.4173 ±13.0 0.7233 【实验仪器】 1.SS495A 型集成霍耳传感器: 工作电压(DC) 4.5 V ~ 5.5 V 磁场测量范围 -67 mT ~ +67 mT(指线性使用范围) 零点电压(零磁场时) 2.500±0.075 V 功耗(在 5V DC 时) 7 mA 灵敏度 K 31.25±1.25 V/T (3.125±0.125 mV/G) 线性误差 100 mm 3.电源和数字电压表: 数字直流恒流源 0 ~ 1000 mA 连续可调,最大输出电压为 20 V 直流稳压电源 0 ~ 20 V 连续可调 四位半数字万用表 200 mV,2 V,20 V DC 档 4.直流分压器和连接导线等.

【实验内容】 1.测量集成蛋耳传感器灵敏度K随工作电压Us的变化.将集成霍耳传感器处于螺线 管内中心点,对于一个给定的工作电压US,测量U6(M=0)和输出电压U(=250mA), 用公式(2)求出K值,M=250mA时,B(x=0)的理论值可通过表1得到.Us取2.5V 至10V.计算K/Us值,并画出K/Us随Us变化图 2.在集成霍耳传感器处于零磁场和Us=5V条件下,将测量线路接成输出电压为零(U。 =0)的补偿电路(即将万用表负端导线接到直流分压器2.4~2.6V输出端,调节电压调 节调旋钮,使得U%=0,为什么?).将集成霍耳传感器处于螺线管内中心点,当螺线管通 过励磁电流M时,在0至500A电流输出范围内,每隔50mA测量集成霍耳传感器的输 出电压U,记录U~M关系数据.从实验结果说明通电螺线管内中心点磁感应强度B(x =0)与霍耳元件产生的霍耳电势差UA之间的关系.注意集成霍耳传感器的输出电压U是 通过霍耳电势差UH信号放大得到的. 3.利用上述测量数据,以通电螺线管中心点磁感应强度B(x=0)的理论计算值为标 准值,校准实验装置上集成霍耳传感器的灵敏度K(用公式(2)求出K值).不同励磁电 流I时螺线管中心点磁感应强度B(x=0)的理论计算值可通过表1得到.另外,也可以 用最小二乘法求出灵敏度K值.由公式(2)和(3),很容易得到U=KC(=O),画出U值 随I变化图,由斜率即可求出K值.将这样确定的灵敏度K值与该产品说明提供的技术 指标比较。 4.测量励磁电流=250A时螺线管内磁场分布,记录输出电压U与位置刻度x的 关系数据,并由此得到磁感应强度B(x)与位置刻度x的关系(灵敏度K用实验内容(3) 确定的值), 5.用作图纸绘出通电螺线管内磁感应强度的实验和理论计算曲线,实验测量数据和理 论计算曲线请分别用实圆点和实线表示,坐标原点选在螺旋管中心处(须对x轴进行坐标 平移). 【注意事项】 1.集成霍耳元件的V+和V极不能接反,否则将损坏元件. 2.仪器接通电源后,应预热数分钟再开始测量数据 3.拆除接线前应先关闭电源. 4.关闭恒流源、稳压电源前,应调节输出电流、电压至零,然后关闭电源. 36
36 【实验内容】 1.测量集成霍耳传感器灵敏度 K 随工作电压 Us 的变化.将集成霍耳传感器处于螺线 管内中心点,对于一个给定的工作电压 Us,测量 U0 (IM = 0)和输出电压 U(IM = 250 mA), 用公式(2)求出 K 值,IM =250 mA 时,B(x = 0)的理论值可通过表 1 得到.Us 取 2.5 V 至 10 V.计算 K/Us 值,并画出 K / Us 随 Us 变化图. 2.在集成霍耳传感器处于零磁场和 Us = 5 V 条件下,将测量线路接成输出电压为零(Uo = 0)的补偿电路(即将万用表负端导线接到直流分压器 2.4 ~ 2.6 V 输出端,调节电压调 节调旋钮,使得 U0 = 0,为什么?).将集成霍耳传感器处于螺线管内中心点,当螺线管通 过励磁电流 IM时,在 0 至 500 mA 电流输出范围内,每隔 50 mA 测量集成霍耳传感器的输 出电压 U,记录 U ~ IM关系数据.从实验结果说明通电螺线管内中心点磁感应强度 B(x = 0)与霍耳元件产生的霍耳电势差 UH之间的关系.注意集成霍耳传感器的输出电压 U 是 通过霍耳电势差 UH信号放大得到的. 3.利用上述测量数据,以通电螺线管中心点磁感应强度 B(x = 0)的理论计算值为标 准值,校准实验装置上集成霍耳传感器的灵敏度 K(用公式(2)求出 K 值).不同励磁电 流 IM时螺线管中心点磁感应强度 B(x = 0)的理论计算值可通过表 1 得到.另外,也可以 用最小二乘法求出灵敏度 K 值.由公式(2)和(3),很容易得到 U = KC (x= 0) IM,画出 U 值 随 IM 变化图,由斜率即可求出 K 值.将这样确定的灵敏度 K 值与该产品说明提供的技术 指标比较. 4.测量励磁电流 IM = 250 mA 时螺线管内磁场分布,记录输出电压 U 与位置刻度 x 的 关系数据,并由此得到磁感应强度 B(x)与位置刻度 x 的关系(灵敏度 K 用实验内容(3) 确定的值). 5.用作图纸绘出通电螺线管内磁感应强度的实验和理论计算曲线,实验测量数据和理 论计算曲线请分别用实圆点和实线表示,坐标原点选在螺旋管中心处(须对 x 轴进行坐标 平移). 【注意事项】 1.集成霍耳元件的 V+和 V- 极不能接反,否则将损坏元件. 2.仪器接通电源后,应预热数分钟再开始测量数据. 3.拆除接线前应先关闭电源. 4.关闭恒流源、稳压电源前,应调节输出电流、电压至零,然后关闭电源.