
试卷代号:2019 座位号■■ 中央广播电视大学2012一2013学年度第二学期“开放专科”期末考试 统计学原理(B) 试题 2013年7月 题 号 三 四 五 总 分 分数 得 分 评卷人 一、单项选择题(从下列每小题的四个选项中,选择一个正确的,将其 顺序号填入题后的括号内,每小题2分,共12分) 1.连续生产的电子管厂,产品质量检验是这样安排的,在一天中,每隔一小时抽取5分钟 的产品进行检验,这是( )。 A.简单随机抽样 B.类型抽样 C.等距抽样 D.整群抽样 2.统计分组的关键是()。 A。正确选择分组标志 B.正确确定组限和组数 C.正确划分分组界限 D.正确选择分组数列的类型 3.直接反映总体规模大小的指标是( )。 A,平均指标 B.相对指标 C.总量指标 D.变异指标 4.抽样调查的主要目的是( A.用样本指标推算总体指标 B.对调查单位作深人研究 C.计算和控制抽样误差 D.广泛运用数学方法 5.相关系数的取值范围是( )。 A.0≤r≤1 B.-1<r<1 C.-1≤r≤1 D.-1≤r≤0 6.根据时期数列计算序时平均数应采用( )。 A.几何平均法 B.加权算术平均法 C.简单算术平均法 D.首末折半法 71
试卷代号 座位号IT] 中央广播电视大学 2 0 3学年度第二学期"开放专科"期末考试 统计学原理 )试题 2013 年7 B.一 B. 型抽 D. B. D.变异指标 B. 调查 D. B. 正确 组 限 D. 组数 D. -1~ :;:;;;; B. D. 首末 半法 一、单项选择题{从下列每小题的四个选项中,选择一个正确的,将其 顺序号填入题后的括号内,每小题 2分,共 2分) 1.连续生产的电子管厂,产品质量检验是这样安排的,在→天中,每隔一小时抽取 5分钟 的产品进行检验,这是( )。 A. C. 抽样 2. 统计分 键是 )。 A. C. 分组界 3. 映总 )。 A. 均指 C. 4. )。 A. 推算 样误 5. )。 A.O:;:;;;;rζl C. -1ζr~三l 6. 据时 算序 A. C. 均法 |题号 - 四l |分数 I I I I I I |得分|评卷人| L I I 71

得分 评卷人 二、多项选择题(以下每小题至少有两项正确答案,全部选对得满分。 多选、少选或错选不得分。每小题2分,本题共8分) 7.下列调查中,调查单位与填报单位一致的有( ). A.工业企业生产设备调查 B.人口普查 C.工业企业现状调查 D.农产量调查 E.城市零售商店销售情况调查 8.下列指标中属于强度相对指标的有( ). A.人口密度 B.平均每人占有粮食产量 C.人口自然增长率 D.人均国内生产总值 E.生产工人劳动生产率 9.在次数分配数列中,( )。 A.各组的频数之和等于100 B.各组的频率大于0 C.频数越小,则该组的标志值所起的作用越小 D.总次数一定,频数和频率成反比 E.频率表明各组标志值对总体的相对作用程度 10.定基发展速度和环比发展速度的关系是( )。 A.两者都属于速度指标 B.环比发展速度的连乘积等于定基发展速度 C.定基发展速度的连乘积等于环比发展速度 D.相邻两个定基发展速度之商等于相应的环比发展速度 E.相邻两个环比发展速度之商等于相应的定基发展速度 得 分 评卷人 三、判断题(判断正误,每小题2分,共10分) 11.在全面工业普查中,全国企业数是统计总体,每个工业企业是总体单位。 () 12.按数量标志分组的目的,就是要区别各组在数量上的差别。 () 13.某企业生产某种产品的单位成本,计划在去年的基础上降低4%,实际降低了3%,则 成本降低计划超额1%完成。 () 14.只有当相关系数接近十1时,才能说明两变量之间存在高度相关关系。 () 15.如果各种商品的销售量平均上涨5%,销售价格平均下降5%,则销售额不变。(·) 72
B. 产量 D. 二、多项选择题{以下每小题至少有两项正确答案,全部选对得满分。 多选、少选或错选不得分。每小题 2分,本题共 8分} 7. 列调 填报单位 )。 A. 工业企业生产设备 查B. c.工业企业现状调查 .农产量调查 E. 店销 情况 8. 下列 强度相 指标 A.人口密度 E. 产率 9. 在 次数分 ( A.各组的频数之和等于 B. C. 频数越 该组 志值 D. 成反 E. 频率 各组 值对 对作用程 10. 定基 展速 A.两者都属于速度指标 B. 发展 连乘 发展速 c.定基发展速度的连乘积等于环比发展速度 D. 邻两 速度之商 发展速度 相邻两 发展 相应 定基发 速度 |得分|评卷人| I I I |得分|评卷人| I I I 三、判断题(判断正误,每小题 2分,共 0分} 1. 面工 数是 工业企业是 ) 12. 各组 数量 ) 13. 企业 某种 单位成本 础上 低4% 了3% 成本降低计划超额 %完成。( ) 14. 数接近+1 两变量之 高度 ) 15. 如果各种 售量平均上涨5% 格平均 降5% 则销 ) 72
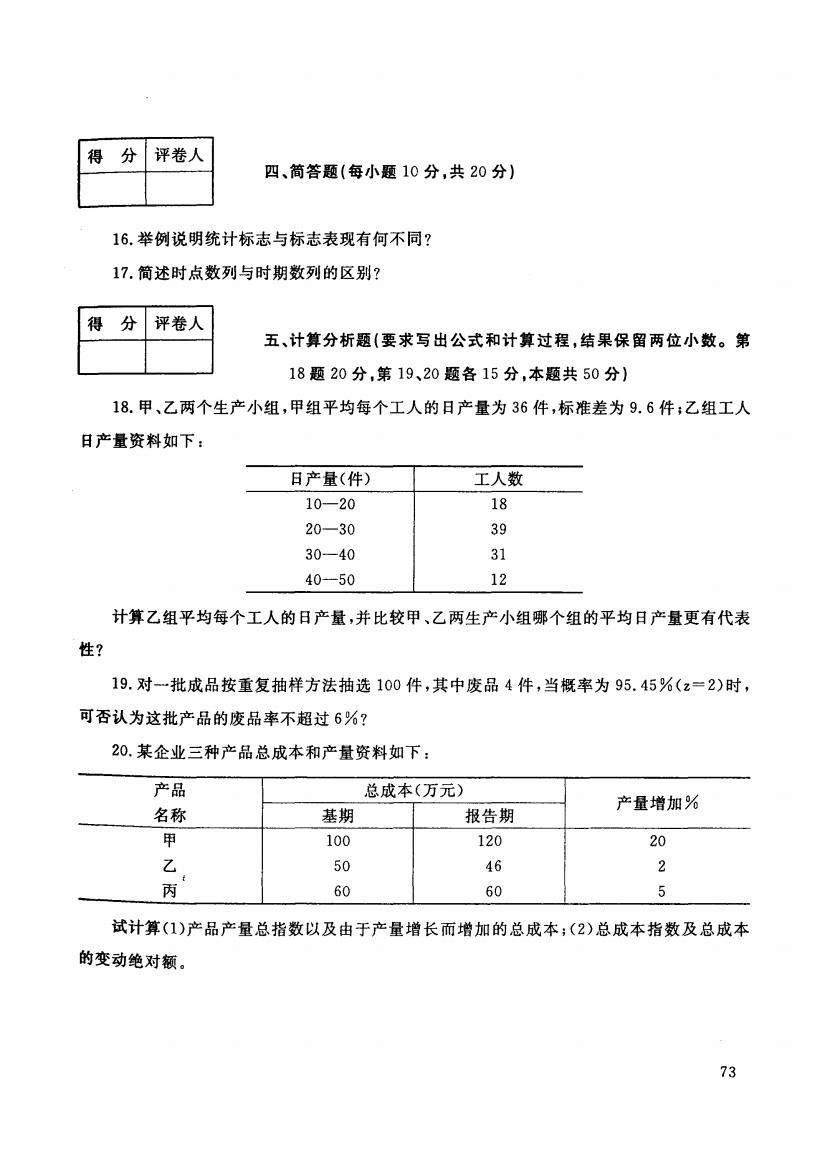
得 分 评卷人 四、简答题(每小题10分,共20分) 16.举例说明统计标志与标志表现有何不同? 17.简述时点数列与时期数列的区别? 得 分 评卷人 五、计算分析题(要求写出公式和计算过程,结果保留两位小数。第 18题20分,第19、20题各15分,本题共50分) 18.甲、乙两个生产小组,甲组平均每个工人的日产量为36件,标准差为9.6件:乙组工人 日产量资料如下: 日产量(件) 工人数 10-20 18 20-30 39 30-40 31 40-50 12 计算乙组平均每个工人的日产量,并比较甲、乙两生产小组哪个组的平均日产量更有代表 性? 19.对-一批成品按重复抽样方法抽选100件,其中废品4件,当概率为95.45%(z=2)时, 可否认为这批产品的废品率不超过6%? 20.某企业三种产品总成本和产量资料如下: 产品 总成本(万元) 产量增加% 名称 基期 报告期 甲 100 120 20 乙 50 46 2 丙 60 60 5 试计算(1)产品产量总指数以及由于产量增长而增加的总成本;(2)总成本指数及总成本 的变动绝对额。 73
得分|评卷人 四、筒答题{每小题 0分,共 0分} 16. 标志 17. 列与 |得分|评卷人| r I I 五、计算分析题{要求写出公式和计算过程,结果保留两位小数。第 18 题20 第19 、20 各15 本题共50 18. 两个 平均 产量为36 为9.6 工人 日产量资料如下 日产量(件) 10-20 I 18 20-30 I 39 30-40 I 31 40-50 I 12 计算乙组平均每个工人的日产量,并比较甲、乙两生产小组哪个组的平均日产量更有代表 性? 19. 对一 按重 抽样方 选100 品4 为95.45%(z=2) 可否认为这批产品的废品率不超过 20. 业三 成本 产品 总成本(万兀) 名称 基期 报告期 产量增加% 100 120 20 50 46 2 60 60 5 试计算(1)产品产量总指数以及由于产量增长而增加的总成本刊 )总成本指数及总成本 的变动绝对额。 73

附页:常用公式 结构相对指标一各组〔或部分)总量 总体总量 比例相对指标=总体中某一部分数值 总体中另一部分数值 比较相对指标一乙单位同类指标值 甲单位某指标值 某种现象总量指标 强度相对指标一另一个有联系而性质不同的现象总量指标 计划完成程度相对指标= 实际完成数 计划任务数 计划完成程度= 计划末期实际达到的水平 计划规定末期应达到的水平 T-22 =2x I=2m =-哥-司-√严 = △.=孙x △p=p n=2说。 N2id2 n-NA:+0 n=p(1-p) Nz2p(1-) △号 n=N△+2b(1- nEzy-ExEy y=√nx=2x)][n2y-(2y叮 y.=a+bx b=12xy-2xEy n∑x2-(∑x)3 a-y-bx s.=√2y-a29-b2 n-2 74
附页:常用公式 一各组(或部分〉总量 结构相对指标一 总体总量 一总体中某一部分数值 比例相对指标一 总体中另一部:frJX-m: 一甲单位某指标值 比较相对指标一 乙单位同类指._~ 某种现象总量指标 强度相对指标= 另一个有联系而性质?一..一.........; --….- 一实际完成数 计划完成程度相对指标一 计划任务数 一计划末期实际达到的水平 计划完成程度一‘. D7 f-u zz z-2d-f -z z-zm-m-z -z f"L, x 2 f σ=....; \. 一/豆豆云 f .. =旦 甘 ~ rfμp- pJ p. l1 (l一是) _ !P(l-P)f1 ....; n ~.=z. .. ~p= z.μp 2 _2 ..,_ 2 _2 zσ 1"'1 n=-.-.- n......" I ~; .• N~;+Z2 z-F-u-AU n N-4hr-z n -N y= n "L, x y - :Ex:E y y' :E 2"] )2 :E -=(:Ey ) 2J yc= α+bx b=n :Exy-~x~y :Ex a= s~=.1 "L,y2 -aL,y-b"L,xy 74

数量指标指数一 po9 ∑po9o 质量指标指数= ∑p94 ∑k9opa 2po91 算术平均数指数= ∑qopo 调和平均数指数= 91p1 9 指数体系: 292=29卫×E9p1 ∑qop, ∑qo0 ∑q1o a=24 n a=2+a:+4+a1+号a 1 n-1 6+2+4+ a=-2 2 ∑f g4.82.8.4an=8 ao a az an-1 ao (a-ao)+(a2-a)+(a3-a2)+A+(an-a-1)=an-ao 平均增长量= 逐期增长量之和累积增长量 逐期增长量个数逐期增长量个数 T=VI an=ao(I)n 75
ar--pu-q =;-z 'E, PIql 质量指标指数一艺五百 指数体系 ÷叶 a= 咛生 +咛生 a= 'E, f _ a c=~b al az a3 • an an ao一一一. "一=- al az an-I ao (al -ao)+ (az -al)+ (a3 -az)+A + (an -an-I) =an-ao 平均增长量一一 -逐期增长量之和-累积增长量 逐期增长量个数逐期增长量个数 '; ll 王=:;f; (x)n 'E, kqoPo 算术平均数指数=一一一一 'E, qoPo 75

试卷代号:2019 中央广播电视大学2012一2013学年度第二学期“开放专科”期未考试 统计学原理(B) 试题答案及评分标准 (供参考) 2013年7月 一、单项选择题(每小题2分,本题共12分) 1.D 2.A 3.C 4.A 5.C 6.C 二、多项选择题(每小题2分,本题共8分) 7.CE 8.ABCD 9.BCDE 10.ABD 三、判断题(判断正误,每小题2分,共10分) 11.× 12.× 13.× 14.X 15.× 四、简答题(每小题10分,共20分) 16.举例说明统计标志与标志表现有何不同? 标志是总体中各单位所共同具有的某特征或属性,即标志是说明总体单位属性和特征的 名称。标志表现是标志特征在各单位的具体表现,是标志的实际体现者。例如:学生的“成绩” 是标志,而成绩为“90”分,则是标志表现。 17.简述时点数列与时期数列的区别? 时期数列是指由反映现象在一段时期内发展过程总量的时期指标构成的动态数列。时点 数列是指由反映现象在某一瞬间总量的时点指标构成的动态数列。二者的区别表现在以下几 个方面: (1)时期数列中各指标的数值是可以相加的,而时点数列中各指标的数值是不能相加的; (2)时期数列中每一个指标数值的大小与所属的时期长短有直接的联系,而时点数列中每 一个指标数值的大小与其时间间隔长短没有直接联系; (3)数列中每个指标的数值,通常是通过连续不断的登记取得的,而时点数列中每个指标 的数值,通常是通过一定时期登记一次而取得的。 76
试卷代号 中央广播电视大学 2 0 3学年度第二学期"开放专科"期末考试 统计学原理 试题 及评 (供参考) 2013 年7 一、单项选择题{每小题 2分,本题共 2分} 1. D 2.A 3. C 4.A S.C 6.C 二、多项选择题{每小题2分,本题共 8分} 7.CE 8. ABCD 9. BCDE 10. ABD 三、判断题(判断正误,每小题 2分,共 0分} 11.X 12. X 13. X 14. X 15. X 四、简答题{每小题 0分,共 0分} 16. 表现有 标志是总体中各单位所共同具有的某特征或属性,即标志是说明总体单位属性和特征的 名称。标志表现是标志特征在各单位的具体表现,是标志的实际体现者。例如 z学生的"成绩" 是标志,而成绩为 " 9 "分,则是标志表现。 17. 时点 的 区 时期数列是指由反映现象在一段时期内发展过程总量的时期指标构成的动态数列。时点 数列是指由反映现象在某一瞬间总量的时点指标构成的动态数列。二者的区别表现在以下几 个方面 (1)时期数列中各指标的数值是可以相加的,而时点数列中各指标的数值是不能相加的; (2) 时期 大小 长短有直接 时点 一个指标数值的大小与其时间间隔长短没有直接联系; (3) 数值 是通过 的数值,通常是通过一定时期登记一次而取得的。 76

五、计算分析题(要求写出公式和计算过程,结果保留两位小数。第18题20分,第19、20题各 15分,本题共50分) 18.(本题20分) 已知甲组x甲=36;0甲=9.6 乙组:元= xf_=15×18+25×39+35×31+45×12=28.7 18+39+31+12 0z= ∑(x-x)了 A ∑f -√西=287刀X18+②5-287×9+35-28.7)X31+45-287X亚 18+39+31+12 =9.13(件) w号80-0,2s7 0z=坚=91=0.318 xz28.7 因为p∠v2,所以甲组的日产量更有代表性。 19.解:n=100,p=4/100=4%,x=2 =包=, 0.04×(1-0.04) =0.0196 n 100 4,=p=2X0.0196=0.039 p士△。=0.04士0.039 即废品率在0.1%一7.9%之间,不能认为废品率是超过6%。 20.解:(1)产品产量总指数 ∑kp9=1.2×100+1.02×50+1.05X60 ∑p9o 100+50+60 234=111.43% 210 由于产量增长而增加的总成本为:∑中90一∑p90=234一210=24(万元) (2)总成本指数 ∑pg 120+46+60=226=107.62% 100+50+60210 总成本的增加值为: ∑p19:-∑p9=226-210=16(万元) 77
五、计算分析题{要求写出公式和计算过程,结果保留两位小数。第 8题 0分,第四、 0题备 15 本题共50 18. (本题 已知甲组王甲 σ甲 X 18 + 25 X 39 + 35 X 31 + 45 X 12 乙组: x= =..LV /,.L V I ~~ /, ~~ I ~~"":': I :J; V "" .L~ = 28.7 、‘ 18 + 39 + 31 + 12 (1 5- 28. 7) 2 X18+(25一28. 7) 瓦于 三H4 三28. 2)(12 18+39+31+ 12 =9.13( -- AU nLpo M-M U 7. 9.13 乙=二:§:::=一,-:=0.318 7 因为 l. 产量更 代表 19. ,ρ=4/100=4 Ap=z,μp=2XO. 0196=0. 039 士~p=O. 04 土0.039 即废品率在 %之间,不能认为废品率是超过 3 ‘hρ 1. 2 X 100 + 1. 02 X 50 + 1. 05 X 60 20. 一一 )'; Poqo 100 + 50 + 60 234 =一~ = 111. 43% 210 由于产量增长而增加的总成本为: ~kPoqo - ~Poqo =234-210=24( …o= ~~~ = 1 >:ρ 100 + 50 + 60 210 总成本的增加值为: ~ρ - ~Poqo =226 77