
§6-5麦克斯伟关系和热系数 理想气体 实际气体 du crdT du dh=c,dT dh ds=Cr+R dv ds= 气体的u,h,s等参数无法直接测量, 实际气体的u,h,s也不能利用理想气体的简单关系, 通常需依据热力学第一、第二定律建立它们与可测参数 的微分关系求解。 上游充通大学 2019年3月23日 3 HANGHAI JLAO TONG UNIVERSITY
2019年3月23日 3 §6–5 麦克斯伟关系和热系数 理想气体 实际气体 g d d d d d d d V p V u c T h c T T v s c R T v d ? d ? d ? u h s 气体的u,h,s等参数无法直接测量, 实际气体的u,h,s也不能利用理想气体的简单关系, 通常需依据热力学第一、第二定律建立它们与可测参数 的微分关系求解

一.全微分(total differential)条件和循环关系 1.全微分判据 设2=z(x,y) 则dz=Mdx+Ndy 其中M= aM ON y Oxoy ( 2.循环关系 若d=0,则 --〔a〔1 3.链式关系 若x,y,z,w中有 =1 两个独立变量,则 上游充通大学 2019年3月23日 4 SHANGHAI JLAO TONG UNIVERSITY
2019年3月23日 4 一.全微分(total differential)条件和循环关系 1.全微分判据 设 z z x y , 则 dz d d , y x z z M x N y M N x y 其中 2.循环关系 若dz=0,则 d d 0 1 y y x x z z z x z y x y x y y x z 2 2 x y M z z N y x y y x x 3.链式关系 若x,y,z,w中有 两个独立变量,则 1 w w w x z z y y x

二.亥姆霍兹函数(Helmholt忆function)和 吉布斯函数(Glibbsian function) 1.亥姆霍兹函数F(比亥姆霍兹函数)一又称自由能 a)定义:F=U-TS;f=u-TB b)因U,T,S均为状态参数,所以F也是状态参数 c)单位J(kJ) d) 物理意义 δg=du+δw→Tds=du+pdv→du=Tds-pdv df=du-Tds-sdT=-sdT-pdv 定温过程-y=∫pdv 所以,可逆定温过程中自由能的减少量是过程膨胀功。 上游充通大学 2019年3月23日 5 HANGHAI JLAO TONG UNIVERSITY
2019年3月23日 5 1.亥姆霍兹函数F(比亥姆霍兹函数 f)—又称自由能 a)定义:F=U–TS;f=u–Ts b)因U,T,S均为状态参数,所以F也是状态参数 c)单位 J ( kJ) d)物理意义 δ d δ d d d d d d d d d d d d q u w T s u p v f u T s s T s v u T s p v T p 二.亥姆霍兹函数(Helmholtz function)和 吉布斯函数(Glibbsian function) 定温过程 2 1 f p v d 所以,可逆定温过程中自由能的减少量是过程膨胀功

2.吉布斯函数G(比吉布斯函数g)一又称自由焓 a)定义:G=H-TSg=h- b)因H,T,S均为状态参数,所以G也是状态参数 c)单位J(kJ) d) 物理意义 δg=dh+δw,→dh=Tds+vdp dg dh-Tds-sdT=-sdT+vdp 定温过程:-g=-∫dp 所以可逆定温过程中自由焓的减少量是过程的技术功。 上游充通大学 2019年3月23日 6 HANGHAI JIAO TONG UNIVERSITY
2019年3月23日 6 2.吉布斯函数G(比吉布斯函数g)—又称自由焓 a)定义:G=H–TS g=h–Ts b)因H,T,S均为状态参数,所以G也是状态参数 c)单位 J (kJ) d)物理意义 δ d δ d d d d d d d d d t q h w g h T h s T s v s T s T v p p 定温过程: 2 1 g v pd 所以可逆定温过程中自由焓的减少量是过程的技术功

三.特性函数 某些状态参数若表示成特定的两个独立参数的函数 时,只需一个状态函数就可以确定系统的其他参数, 这样的函数称之为“特性函数”。如 u=u(s,v);h=h(s,p);fAT,v)Bg=g(p,T), 例 u=u(s,v) Bu du S as) dv 与du=Tds-pdv比较: T= p=- 上游充通大粤 2019年3月23日 7 SHANGHAI JLAO TONG UNIVERSITY
2019年3月23日 7 三.特性函数 某些状态参数若表示成特定的两个独立参数的函数 时,只需一个状态函数就可以确定系统的其他参数, 这样的函数称之为“特性函数”。如 u=u(s,v); h=h(s,p);f=f(T,v) 及 g=g(p,T), 例 , d d d v s u u u u s v u s v s v 与 比较: d d d u T s p v v s u u T p s v

根据 h=u+pv h=u-v 8 Ou f=u-Ts f=u-s Ou g=h-Ts 8=-m, 特性函数建立了各种热力学函数之间的简要关系 上游充通大粤 2019年3月23日 8 SHANGHAI JLAO TONG UNIVERSITY
2019年3月23日 8 根据 s v v s s u s v u g h Ts g u v s u f u Ts f u s v u h u p v h u v 特性函数建立了各种热力学函数之间的简要关系
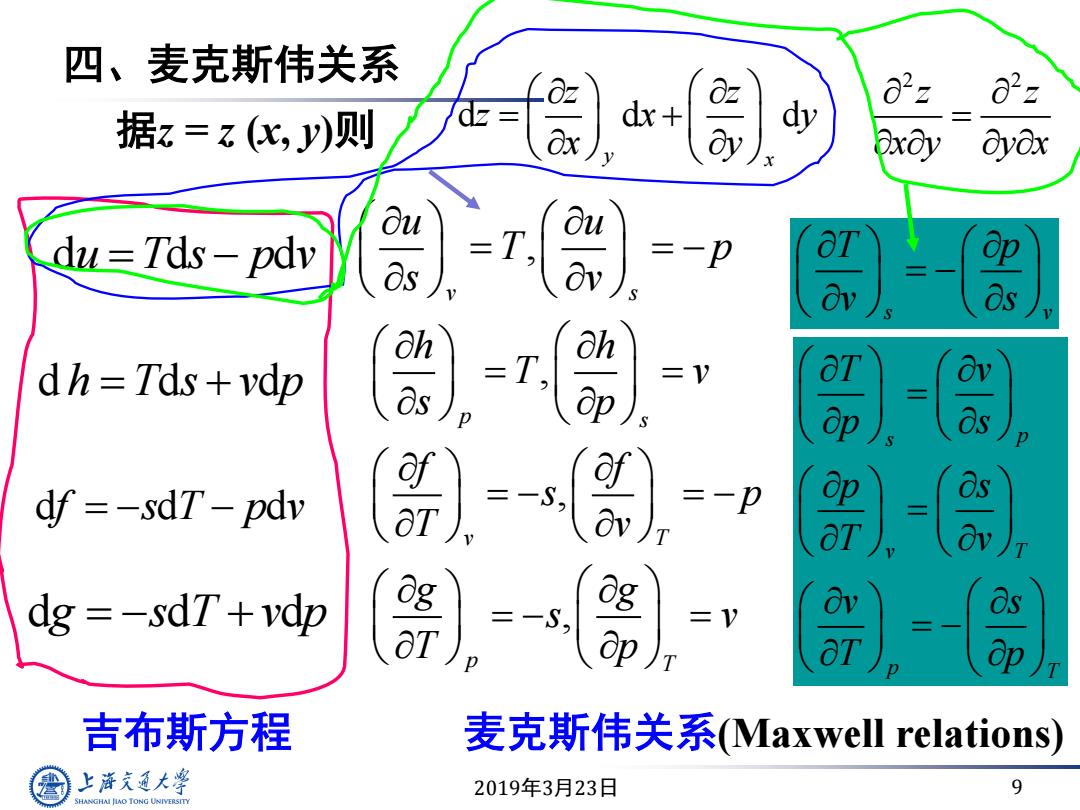
四、麦克斯伟关系 .0z 据z=z(化,y)则 dx+ ax) axoy ayox du=Tds-pdv -p dh=Tds vdp ) p =V a df =-sdT-pdv =-p 江 dg =-sdT+vdp 8) g =V p 吉布斯方程 麦克斯伟关系(Maxwell relations) 上降文通大学 2019年3月23日 9 SHANGHAI JIAO TONG UNIVERSITY
2019年3月23日 9 四、麦克斯伟关系 据z = z (x, y)则 2 2 d d d y x z z z z z x y x y x y y x d d d u T s p v , v s u u T p s v s v T p v s 吉布斯方程 麦克斯伟关系(Maxwell relations) d d d h T s v p d d d f s T p v d d d g s T v p , , , p s v T p T h h T v s p f f s p T v g g s v T p s p v T p T T v p s p s T v v s T p

助忆图 器 =V S =V 器 h S -S =T T→ 8s 1 落脚在p和s的都有负号 上游充通大学 2019年3月23日 10 SHANGHAI JLAO TONG UNIVERSITY
2019年3月23日 10 助忆图 p s T v T T v p v s p s T v s v s p v T p s T v h f g u v p g T s T f v T s u v T T v p v s v p g T 落脚在p和s的都有负号

例题第六章A322343 有一种气体,当体积保持固定时,其压力正比于 绝对温度T,试证明此气体的熵随体积而增加,即 8s 证:由题意体积固定时pcT,故气体服从p=孔v)T 根据麦氏关系 p S 因气体p>0,TP0 T T [fp门 0 即 即气体的熵随体积增大而增大 p T 上游充通大学 2019年3月23日 11 SHANGHAI JIAO TONG UNIVERSITY
2019年3月23日 11 有一种气体,当体积保持固定时,其压力p正比于 绝对温度T,试证明此气体的熵随体积而增加,即 0 T v s 证:由题意 体积固定时pT,故气体服从p=f(v)T 根据麦氏关系 T T v p v s 因气体p>0,T>0 0 0 T p s T v 即 即气体的熵随体积增大而增大 p s T v f v T T f v T p 例题\第六章\A322343

例题第六章4320254 某种气体服从p(v-b)=RT,式中b为常数,若其比热 c为定值,试证明内能U只是温度的函数。 证: 取U=f(V,T) dU dV 己知cv= aU dU=crdT+ (A) dU=Tds-pdv (B) p S as (C) T RT p= 号 v-b (D) 上游充通大粤 2019年3月23日 12 SHANGHAI JLAO TONG UNIVERSITY
2019年3月23日 12 某种气体服从 p(v-b)=RgT,式中b为常数,若其比热 cV为定值,试证明内能U只是温度的函数。 证: , d d d V T U U U f V T U T V T V 取 V V d d d V T U U c U c T V A T V 已知 p s T v d d d T T U S U T s p V T p B V V C T p V S T V g g V R T R p p p D v b T v b T 例题\第六章\A320254