上海交通大学：《热力系统设计与实践 Design and Practice of Thermodynamic System》课程教学资源（2018课件）第03讲 实际气体性质及热力学一般关系式 Behavior of real gases and generalized thermodynamic relationships（压缩因子与范德瓦尔方程等）

第6章 实际气体性质及热力学一做关系式 (Behavior of real gases and generalized thermodynamic relationships) 上游充通大学 2018年3月9日 2 SHANGHAI JLAO TONG UNIVERSIT

2018年3月9日 2 第 6 章 实际气体性质及热力学一般关系式 (Behavior of real gases and generalized thermodynamic relationships)

6-1理想气体状态方程用于实际气体偏差 1.5 35K(63R) 理想气体pN=RT pV=1 50K(90R) R,T 100K(180R) 60K(108R) 200K(360°R) 1.0 实际气体pv=ZRT 300K(540R) 压缩因子(compressibility)Z Z= pv R 100 200 >1 p (atm) Z= =1 氢不同温度时压缩因子 <1 与压力关系 上游通大学 2018年3月9日 3 SHANGHAI JLAO TONG UNIVERSITY

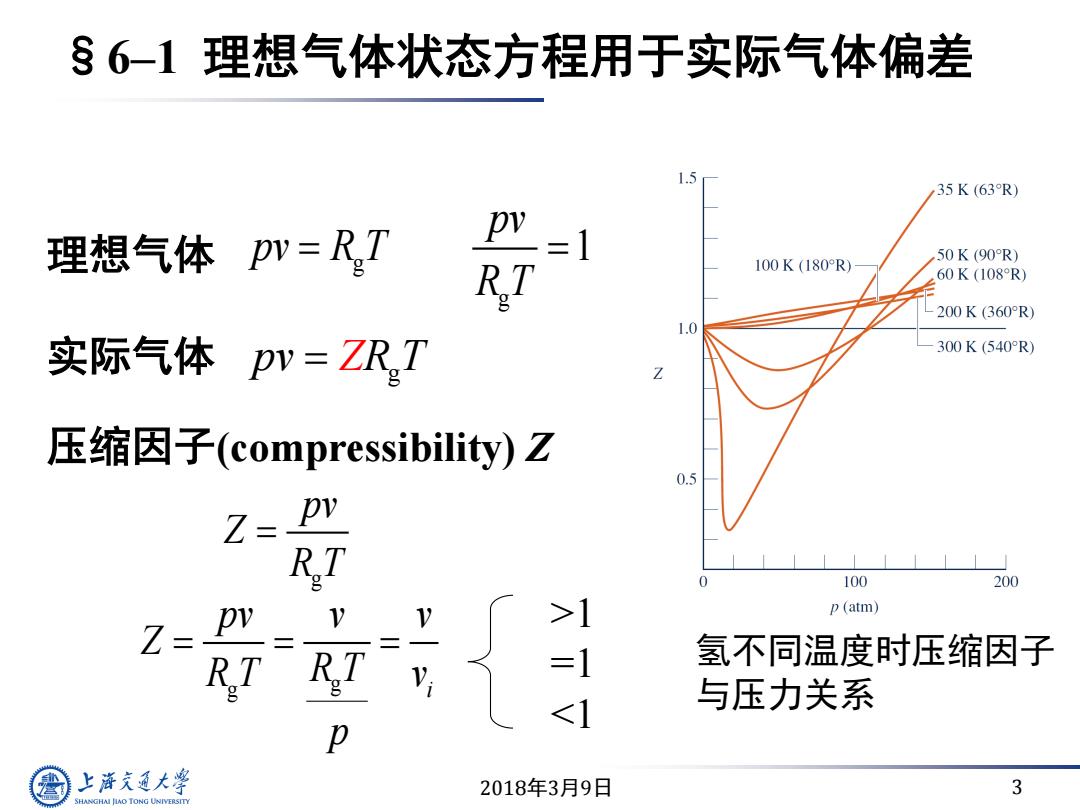
2018年3月9日 3 §6–1 理想气体状态方程用于实际气体偏差 理想气体 g g 1 pv pv R T R T   实际气体 g pv T  ZR 压缩因子(compressibility) Z g g i pv v v Z R T v R T p    >1 =1 <1 g pv Z R T  氢不同温度时压缩因子 与压力关系

rf 方（斥力） r=6f=0分子当量作用半径 4 %=2元3=4×1030m3 3 方1（引力） r>r f>0 -分子有效作用半径 在标准状态下(p-1atm,273.15K) Vm=22.4×10-3m3/mol 有6.02×1023个分子 V=6.02×1023×4×1030=2.4×106m3/mol =1.07x104( 分子自身所占的比例) m 上游充通大学 2018年3月9日 4 SHANGHAI JIAO TONG UNIVERSITY

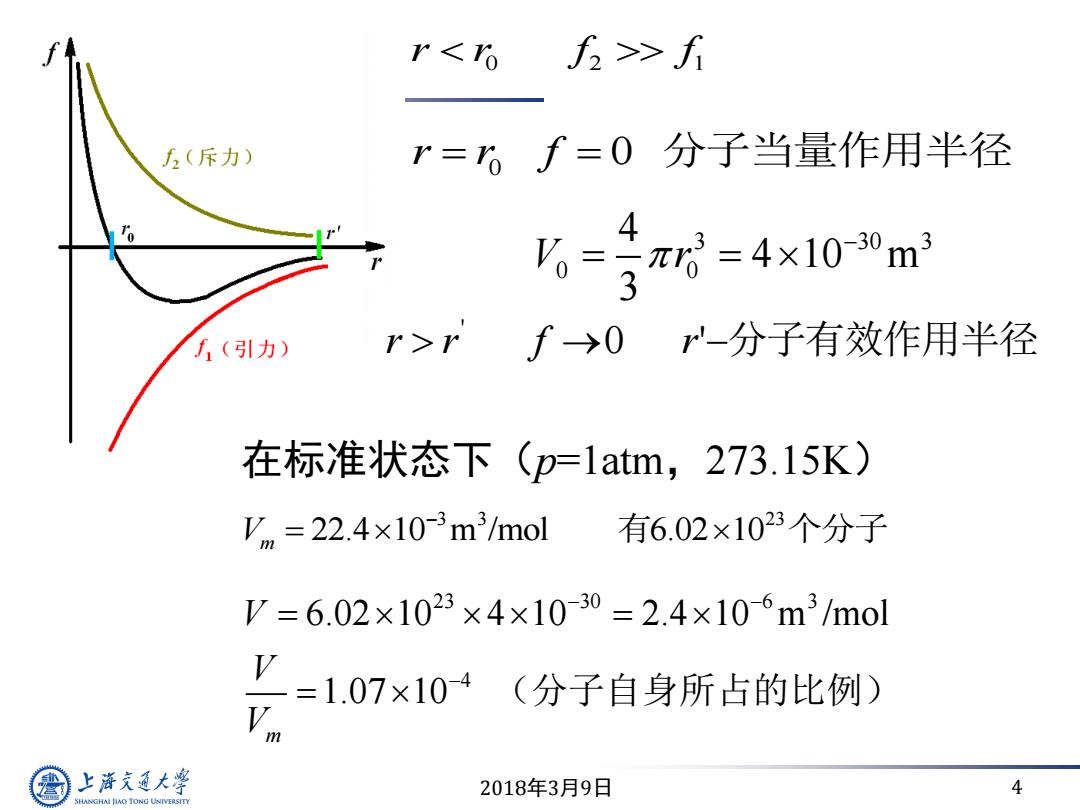
2018年3月9日 4 0 2 1 r r f f   在标准状态下（p=1atm，273.15K） 3 3 23 22.4 10 m /mol 6.02 10 Vm     有 个分子 23 30 6 3 4 6.02 10 4 10 2.4 10 m /mol 1.07 10 m V V V            （分子自身所占的比例） r r f   0 0 分子当量作用半径 3 30 3 0 0 4 4 10 m 3 V r      r  r ' f 0 r'分子有效作用半径

§6-2范德瓦尔方程和R-K方程 一.范德瓦尔方程 (Jahanns Diderik Van der Waals,1873) m-8r一+2时 或p RT a,b物性常数 V.-b v2 a 气态物质较小； 内压力 液态，如水20C时1.05×108Pa (分子引力引起，气体实际施加于壁面的压力比理想气体压力小) (Vmb)一分子自由活动的空间 b-气体体积V中包含气体分子本身的总体积 又称协体积(Covolume) 上游究通大粤 2018年3月9日 5 SHANGHAI JLAO TONG UNIVERSITY

2018年3月9日 5 §6–2 范德瓦尔方程和R-K方程 一.范德瓦尔方程 V b RT V a p m m            2 a, b—物性常数 2 Vm a 内压力 （分子引力引起，气体实际施加于壁面的压力 比 理想气体压力小） 气态物质较小； 液态，如水20℃时1.05×108Pa (Vm–b)—分子自由活动的空间 b – 气体体积V中包含气体分子本身的总体积 又称协体积（Covolume） g pv R T  (Jahanns Diderik Van der Waals, 1873) 2 m m RT a p V b V    或

范氏方程的评价 范氏方程： 1)定性反映气体 p-y-T关系； 范氏方程展开后是体积的立方型方程 2)远离液态时， 即使压力较高，计 算值与实验值误差 C02 323K 较小。如N,常温下 10 350K 100MPa时无显著误 8 304 ed,Ol/d 差。在接近液态时， 误差较大，如C0,常 温下5MPa时误差约 273.16K 4%,100MPa时误差 35%; 0.2 0.4 0.6 3)巨大理论意义 'm/(10-3m3.mol-l ap a >0没有物理意义 上泽充通大 2018年3月9日 6 SHANGHAI JIAO TONG UNIVERSITY

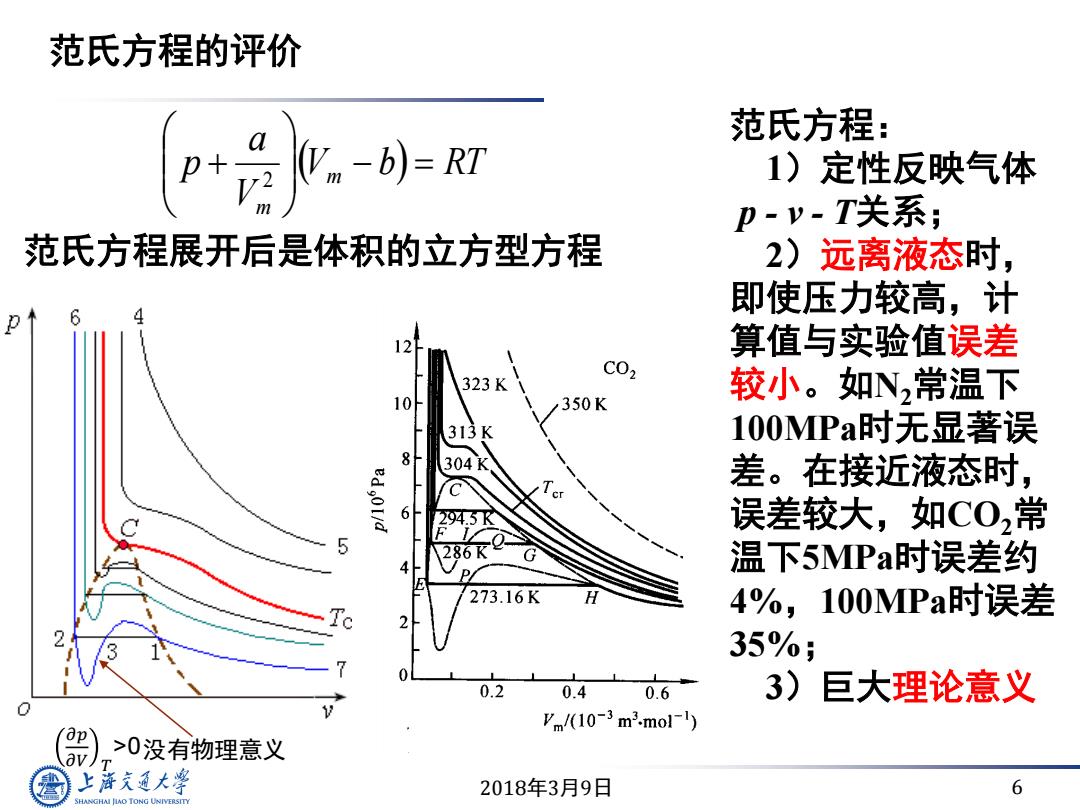
2018年3月9日 6 范氏方程： 1）定性反映气体 p - v - T关系； 2）远离液态时， 即使压力较高，计 算值与实验值误差 较小。如N2常温下 100MPa时无显著误 差。在接近液态时， 误差较大，如CO2常 温下5MPa时误差约 4%，100MPa时误差 35%； 3）巨大理论意义 范氏方程展开后是体积的立方型方程 范氏方程的评价 V b RT V a p m m            2 没有物理意义 𝜕𝑝 𝜕𝑉 𝑇 >0

p 范德瓦尔常数a,b求法 1)利用p、y、T实测数据拟合； 2)利用通过临界点c的等温线 性质求取： RT 临界点p、y、T值满足范氏方程 V-b p =0 迎 RT. 2a (Vm-b) =0 mc =0 2RT. 6a )(U-by 27RT2 b= 1RT a= R= 64 Pe 8 Pc 3 T. 上游充通大学 2018年3月9日 7 SHANGHAI JIAO TONG UNIVERSITY

2018年3月9日 7 范德瓦尔常数a，b求法 1）利用p、v、T实测数据拟合; 2）利用通过临界点c的等温线 性质求取: 临界点p、v、T值满足范氏方程 2 mc mc c c V a V b RT p      0 2 0 2 3                       mc mc c T T V a V b RT v p v p c c 2 2 27 1 8 64 8 3 c c c mc c c c R T RT p V a b R p p T      0 2 6 0 2 3 4 2 2 2                          mc mc c T T V a V b RT v p v p c c

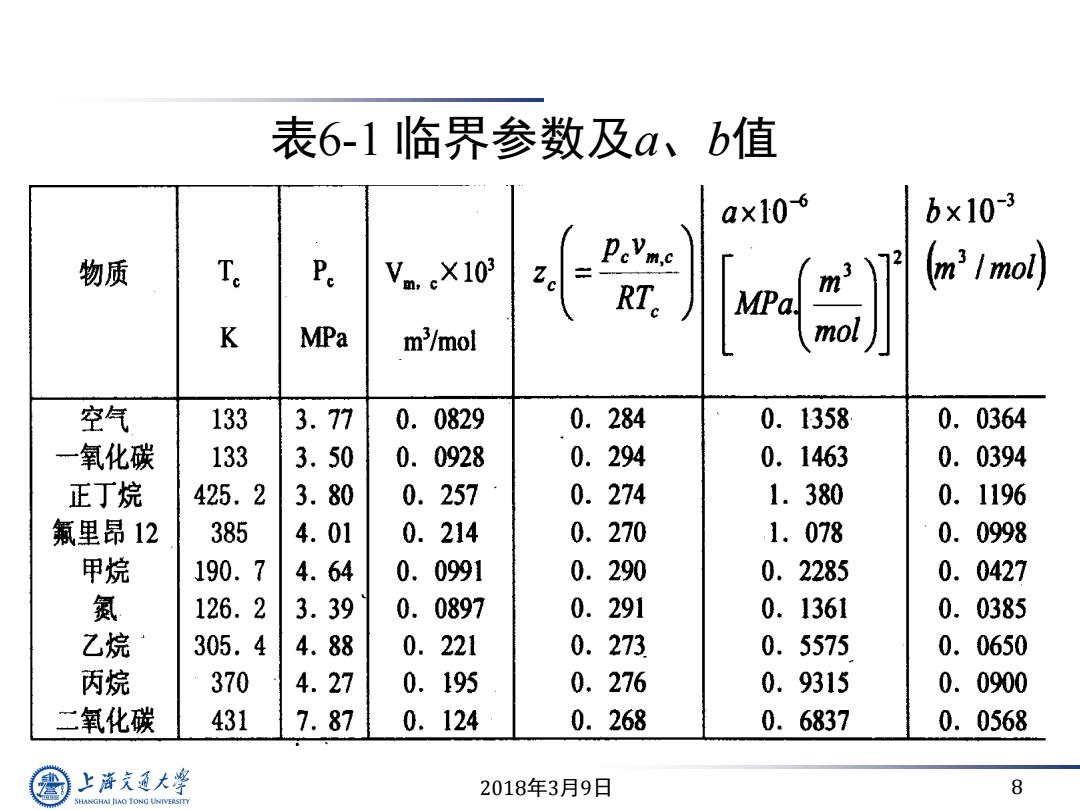
表6-1临界参数及a、b值 ax106 b×10-3 物质 Te Pe Vm.X103 Zc K MPa m'/mol 空气 133 3.77 0. 0829 0.284 0.1358 0.0364 氧化碳 133 3.50 0.0928 0.294 0.1463 0.0394 正丁烷 425.2 3.80 0.257 0.274 1.380 0.1196 氟里昂12 385 4.01 0.214 0.270 1.078 0. 0998 甲烷 190.7 4.64 0.0991 0.290 0.2285 0.0427 氮 126.2 3.39 0.0897 0.291 0.1361 0.0385 乙烷 305.4 4.88 0.221 0.273 0.5575 0. 0650 丙烷 370 4.27 0.195 0.276 0.9315 0.0900 二氧化碳 431 7.87 0.124 0.268 0.6837 0.0568 上游充通大学 2018年3月9日 8 SHANGHAI JIAO TONG UNIVERSITY

2018年3月9日 8 表6-1 临界参数及a、b值

更多流体的临界参数 Critical-point properties Gas Molar mass, constant, Temperature, Pressure, Volume, Substance Formula M kg/kmol R kJ/kg·K K MPa m3/kmol Air 28.97 0.2870 132.5 3.77 0.0883 Ammonia NH3 17.03 0.4882 405.5 11.28 0.0724 Argon Ar 39.948 0.2081 151 4.86 0.0749 Benzene CeHs 78.115 0.1064 562 4.92 0.2603 Bromine Br2 159.808 0.0520 584 10.34 0.1355 n-Butane CaHio 58.124 0.1430 425.2 3.80 0.2547 Carbon dioxide C02 44.01 0.1889 304.2 7.39 0.0943 Carbon monoxide Co 28.011 0.2968 133 3.50 0.0930 Carbon tetrachloride CCI4 153.82 0.05405 556.4 4.56 0.2759 Chlorine Cl2 70.906 0.1173 417 7.71 0.1242 Chloroform CHCI3 119.38 0.06964 536.6 5.47 0.2403 Dichlorodifluoromethane(R-12) CCI2F2 120.91 0.06876 384.7 4.01 0.2179 Dichlorofluoromethane(R-21) CHCIF 102.92 0.08078 451.7 5.17 0.1973 Ethane C2H5 30.070 0.2765 305.5 4.48 0.1480 Ethyl alcohol C2HOH 46.07 0.1805 516 6.38 0.1673 Ethylene C2Ha 28.054 0.2964 282.4 5.12 0.1242 Helium He 4.003 2.0769 5.3 0.23 0.0578 n-Hexane C6H14 86.179 0.09647 507.9 3.03 0.3677 Hydrogen (normal) H2 2.016 4.1240 33.3 1.30 0.0649 Krypton 83.80 0.09921 209.4 5.50 0.0924 Methane CHa 16.043 0.5182 191.1 4.64 0.0993 Methyl alcohol CHOH 32.042 0.2595 513.2 7.95 0.1180 Methyl chloride CHCI 50.488 0.1647 416.3 6.68 0.1430 Neon N 20.183 0.4119 44.5 2.73 0.0417 Nitrogen N2 28.013 0.2968 126.2 3.39 0.0899 Nitrous oxide 20 44.013 0.1889 309.7 7.27 0.0961 Oxygen 02 31.999 0.2598 154.8 5.08 0.0780 Propane CaH8 44.097 0.1885 370 4.26 0.1998 Propylene C3H6 42.081 0.1976 365 4.62 0.1810 Sulfur dioxide S02 64.063 0.1298 430.7 7.88 0.1217 Tetrafluoroethane(R-134a) CFCH>F 102.03 0.08149 374.2 4.059 0.1993 Trichlorofluoromethane (R-11) CCIaF 137.37 0.06052 471.2 4.38 0.2478 Water H20 18.015 0.4615 647.1 22.06 0.0560 Xenon e 131.30 0.06332 289.8 5.88 0.1186 "The unit kJ/kg.K is equivalent to kPa.m/kg.K.The gas constant is calculated from R-R/M,where R-8.31447 kJ/kmol.K and M is the molar ma55. Source:K.A.Kobe and R.E.Lynn.Jr..Chemical Review 52 (1953).pp.117-236:and ASHRAE.Handbook of Fundamentals (Atlanta,GA:American Society of Heating.Refrigerating and Air-Conditioning Engineers,Inc.,1993),pp.16.4 and 36.1 上通大学 2018年3月9日 9 SHANGHAI JIAO TONG UNIVERSITY

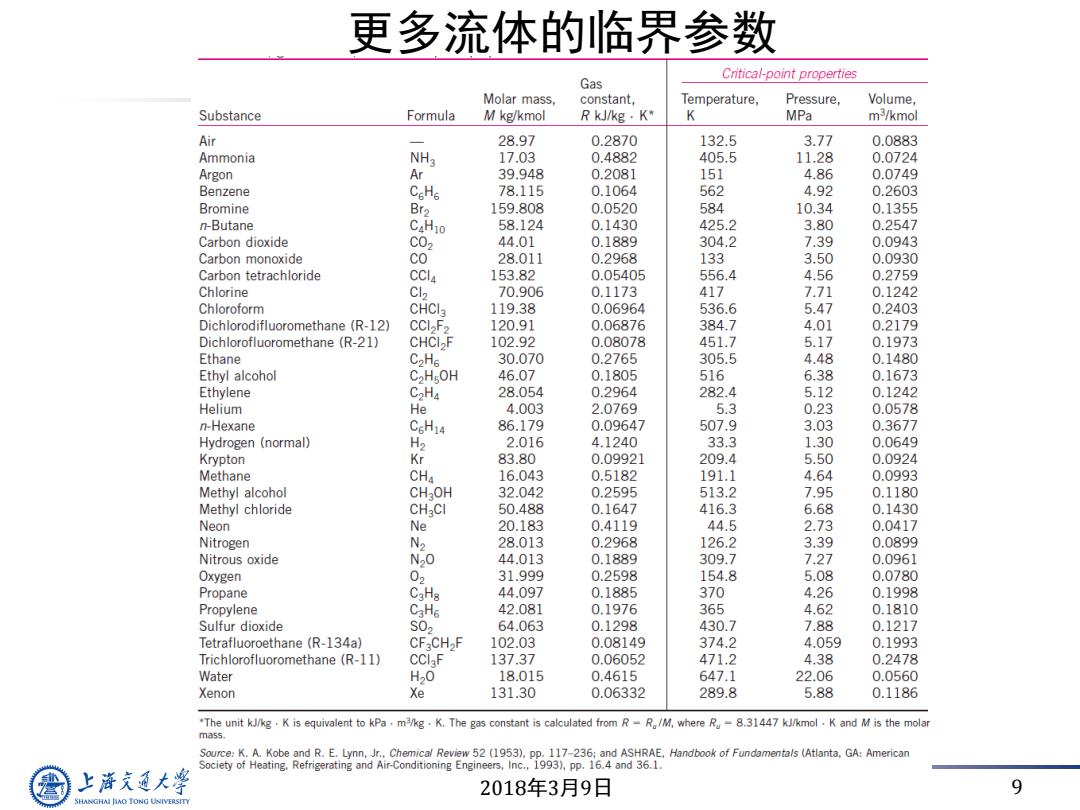
2018年3月9日 9 更多流体的临界参数

按以上分析结果，对任何范德瓦尔气体，都有 a ×3b 2762 3 0.375 RgTe 8 a 8 27R.b 事实表明，对于不同的气体上述比值并不相同： 对理想气体，该值应等于1； 对大多数实际气体，该值都远小于0.375， 范德瓦尔方程在定量说明实际气体热力性质方面不够成功！ 上游充通大学 2018年3月9日 10 SHANGHAI JLAO TONG UNIVERSITY

2018年3月9日 10 按以上分析结果，对任何范德瓦尔气体，都有 事实表明，对于不同的气体上述比值并不相同： 对理想气体，该值应等于1； 对大多数实际气体，该值都远小于0.375， 范德瓦尔方程在定量说明实际气体热力性质方面不够成功！

二、R-K方程(Redlich-Kwong,1949) RT a p 修正压力项 V-b ToV V+b) →精度提高 a,b_物性常数 1)由p,v,T实验数据拟合； 2)由临界参数求取 0.427480R2T25 0.08664RT a= b= Pe 对于气液相平衡和混合物的计算符合总体很好。但液相密度误差大。 比较适用于简单物质如Ar,Kr,N2,02,C0,CH4等 →Wi l son方程、SRK方程 上游充通大学 2018年3月9日 11 HANGHAI JLAO TONG UNIVERSITY

2018年3月9日 11 二、R-K方程 (Redlich-Kwong，1949) T V V b a V b RT p m m m     0.5 a, b—物性常数 1）由p，v，T实验数据拟合； 2）由临界参数求取 c c c c p RT b p R T a 0.427480 0.08664 2 2.5    Wilson方程、SRK方程 修正压力项 精度提高 对于气液相平衡和混合物的计算符合总体很好。但液相密度误差大。 比较适用于简单物质如Ar，Kr，N2，O2，CO，CH4等