上海交通大学：《热力系统设计与实践 Design and Practice of Thermodynamic System》课程教学资源（2017课件）第09讲 理想气体混合物及湿空气 Ideal gas mixture and moisture（湿空气热物性）

2 第12章 理想气体混合物及湿空气 (deal gas mixture and moisture) 上游充通大粤 Mar/14,2017 2 HANGHAI JLAO TONG UNIVERSIT

Mar/14, 2017 2 2 第 12 章 理想气体混合物及湿空气 (Ideal gas mixture and moisture)

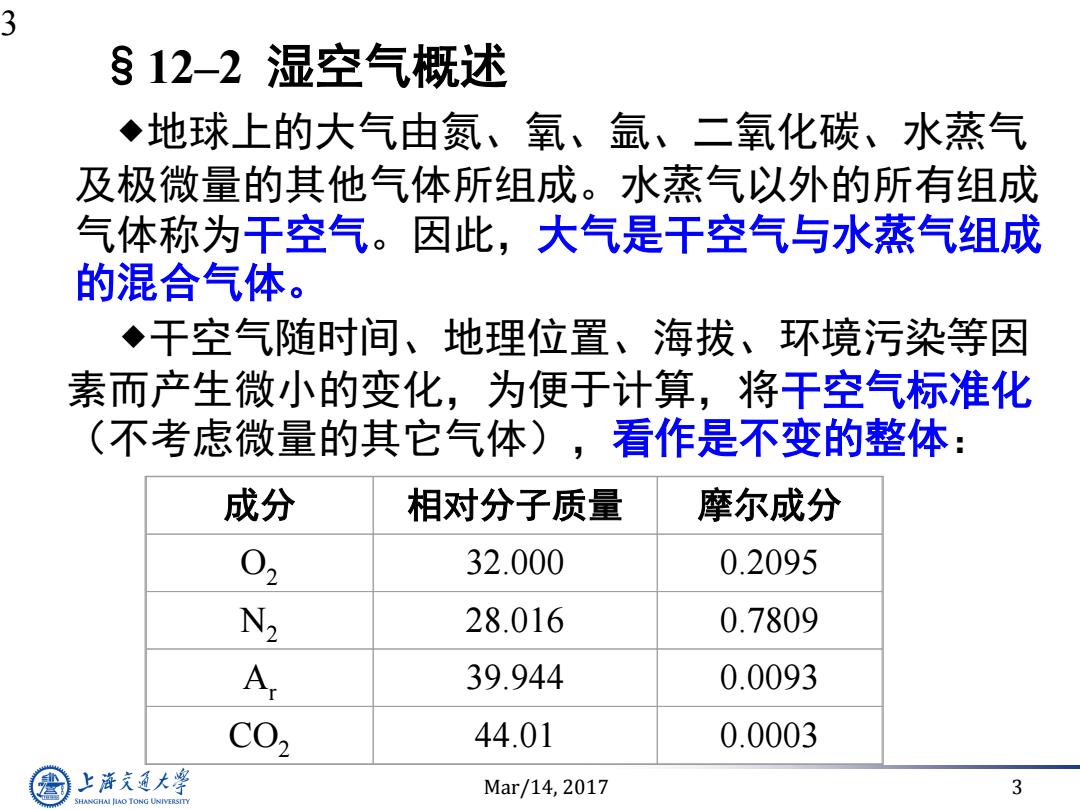
3 §12-2湿空气概述 ◆地球上的大气由氮、氧、氩、二氧化碳、水蒸气 及极微量的其他气体所组成。水蒸气以外的所有组成 气体称为干空气。因此，大气是干空气与水蒸气组成 的混合气体。 ◆干空气随时间、地理位置、海拔、环境污染等因 素而产生微小的变化，为便于计算，将干空气标准化 (不考虑微量的其它气体)，看作是不变的整体： 成分 相对分子质量 摩尔成分 02 32.000 0.2095 N, 28.016 0.7809 A 39.944 0.0093 C02 44.01 0.0003 上游充通大学 Mar/14,2017 3 SHANGHAI JIAO TONG UNIVERSITY

Mar/14, 2017 3 3 §12–2 湿空气概述 地球上的大气由氮、氧、氩、二氧化碳、水蒸气 及极微量的其他气体所组成。水蒸气以外的所有组成 气体称为干空气。因此，大气是干空气与水蒸气组成 的混合气体。 干空气随时间、地理位置、海拔、环境污染等因 素而产生微小的变化，为便于计算，将干空气标准化 （不考虑微量的其它气体），看作是不变的整体： 成分 相对分子质量 摩尔成分 O2 32.000 0.2095 N2 28.016 0.7809 Ar 39.944 0.0093 CO2 44.01 0.0003

4 湿空气=干空气(dry air)+ p=pa+p 水蒸气(water vapor) R R 湿空气是理想气体混合物 M 一.未饱和湿空气(unsaturated air)和 饱和湿空气(saturated air) 过热t>t,（p,)空气未饱和 空气中的水蒸气 (t,p)饱和t=t,（p,)空气饱和 所以空气饱和与否取决于t,P, 上游通大学 Mar/14,2017 4 HANGHAI JLAO TONG UNIVERSITY

Mar/14, 2017 4 4 湿空气=干空气(dry air) + 水蒸气(water vapor) 湿空气是理想气体混合物 a v p p p   一.未饱和湿空气(unsaturated air)和 饱和湿空气(saturated air) t t p  s v   所以空气饱和与否取决于t，pv g R R M  空气中的水蒸气 t t p  s v   过热 空气未饱和 （t，pv） 饱和 空气饱和

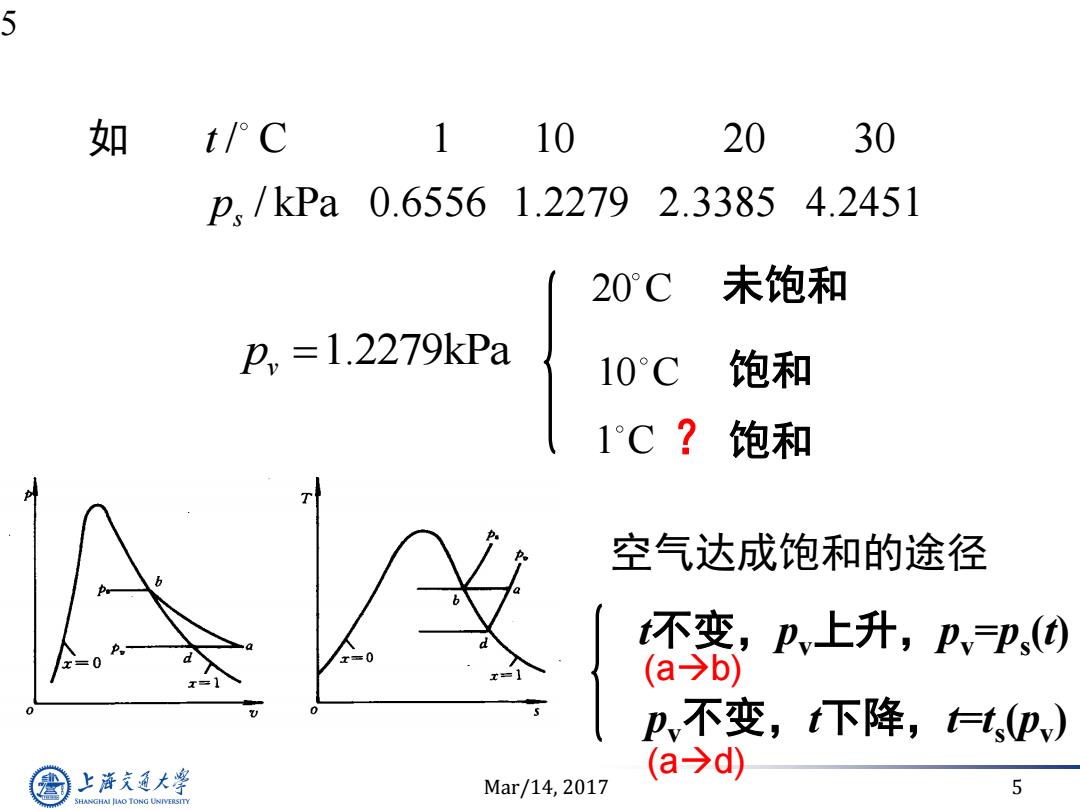
5 如 t/°C 1 10 20 30 p,/kPa 0.65561.2279 2.33854.2451 20°C 未饱和 p,=1.2279kPa 10°C饱和 1°C?饱和 空气达成饱和的途径 t不变，pv上升，p=P、() (a→b) p,不变，t下降，t) 上游究通大粤 (a→d Mar/14,2017 5 SHANGHAI JLAO TONG UNIVERSITY

Mar/14, 2017 5 5 如 / C 1 10 20 30 / kPa 0.6556 1.2279 2.3385 4.2451 s t p 1.2279kPa v p  20 C 10 C 未饱和 饱和 1 C ？ 饱和 空气达成饱和的途径 t不变，pv上升，pv =ps (t) pv不变，t下降，t=t s (pv ) (ad) (ab)

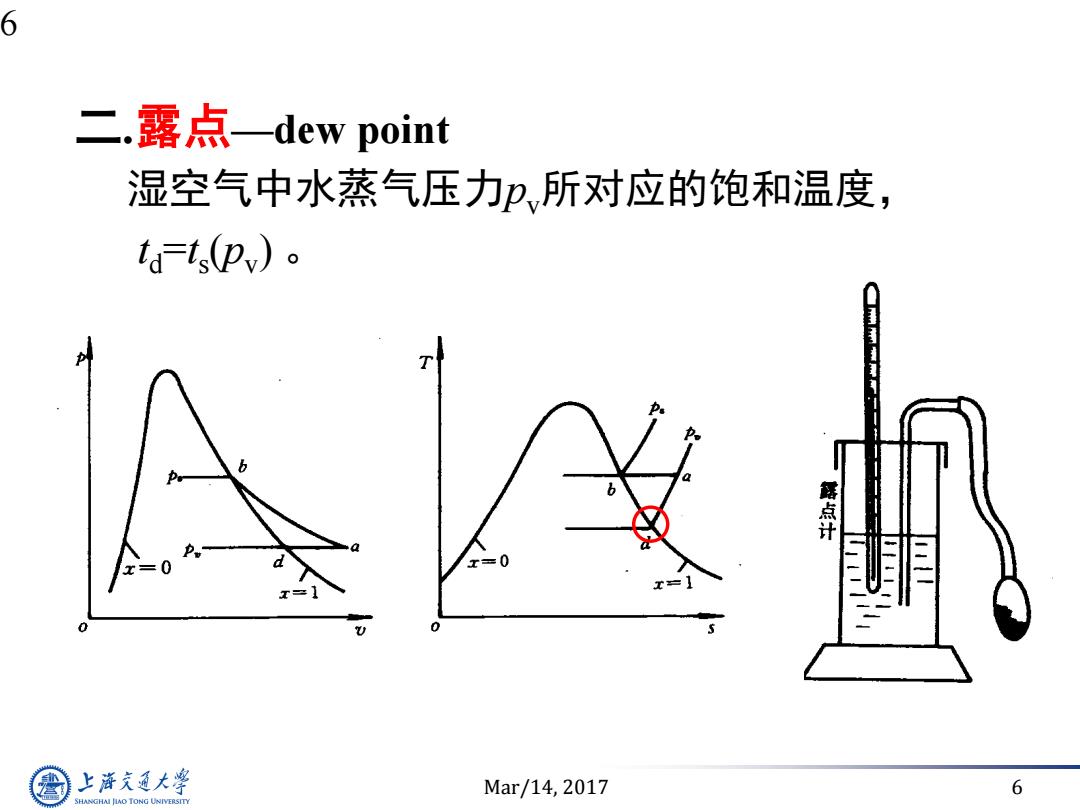
6 二.露点一dew point 湿空气中水蒸气压力，所对应的饱和温度， ta=tpv)。 点计 x=0 上净充通大学 Mar/14,2017 6 SHANGHAI JLAO TONG UNIVERSITY

Mar/14, 2017 6 6 二.露点—dew point 湿空气中水蒸气压力pv所对应的饱和温度， td =t s (pv )

例题1第十二章A422144 氢气和水蒸气混合物中容积成分如下： pH=0.965,p1o=0.035混合物的总压力p=0.15MPa 假定该混合物被等压冷却到20°℃，求露点温度和终态 时气相部分的容积成分。 解： 根据理想气体混合物性质，= X= p p,=x,p=0.035×0.15MPa=0.00525MPa=5.25kPa 在露点温度时，水蒸气的饱和压力等于5.25kPa,查表 得：t=33.8C 因为20℃〈t,所以20℃时是饱和湿空气。 P,20c=P20c=2.34kPa=0.00234MPa 此时PH,=p-P,20c=0.15MPa-0.00234MPa=0.14766MPa P=0.9844 XH,0,汽= P20c=0.0156 p 上游气通大学 Mar/14,2017 7 HANGHAI JIAO TONG UNIVERSITY

Mar/14, 2017 7 氢气和水蒸气混合物中容积成分如下： φH2=0.965， φH2O=0.035混合物的总压力p=0.15MPa 假定该混合物被等压冷却到20℃，求露点温度和终态 时气相部分的容积成分。 解：根据理想气体混合物性质 i i p x p  v v p x p      0.035 0.15MPa 0.00525MPa 5.25kPa 在露点温度时，水蒸气的饱和压力等于5.25kPa，查表 得：td=33.8℃ v,20 C ,20 C 2.34kPa 0.00234MPa s p p    此时 H2 ,20 C 0.15MPa 0.00234MPa 0.14766MPa v p p p      2 2 2 H ,20 C H H O, 0.9844 0.0156 v p p x x p p     汽 i i x  例题\第十二章\A422144 因为20℃ < td，所以20℃时是饱和湿空气

8 §12-3相对湿度(the relative humidity)和 含湿量(humidity;humidity ratio) 一绝对湿度(absolute humidity)pv 每立方米湿空气中水蒸气的质量kg/m3 所以 1)P,P, PK-RT31-A 2)p,≤pv.max=Ps Pv≤P3=Pv,max=p' 3)P数值不能直接反映湿空气吸湿能力的大小 如pv=0.6566kPa,1C时p,=ps,无吸湿能力 10C时p,<p,有吸湿能力。 上游充通大学 Mar/14,2017 8 HANGHAI JLAO TONG UNIVERSITY

Mar/14, 2017 8 8 §12-3 相对湿度(the relative humidity)和 含湿量(humidity; humidity ratio) 一.绝对湿度(absolute humidity) ρv 每立方米湿空气中水蒸气的质量 kg/m3 所以 v v v v v gv v v gv 1 1) p p p v R T v R T              3）ρv数值不能直接反映湿空气吸湿能力的大小 如pv=0.6566kPa，1℃时pv =ps，无吸湿能力 10℃时pv <ps有吸湿能力。 v v,max v v,max 2) '' s s p p p         

9 二、相对湿度 (饱和度)-humidity 一湿空气中水蒸气含量与同温度下最大可能含量之比。 1) Ps Py=ps P Vs 2) p=0 干空气 吸湿 0≤0≤1 0t(p), 如在1atm时，t>100C时， 由于水蒸汽的最大压力（饱和压力）p、>p,故 Pv,max=p<P此时 Pv.max 上游究通大学 Mar/14,2017 9 SHANGHAI JLAO TONG UNIVERSITY

Mar/14, 2017 9 9 二、相对湿度（饱和度）-- humidity —湿空气中水蒸气含量与同温度下最大可能含量之比。 v s     v s p p   0 1    =0 干空气 0 t s（p），如在1atm时，t > 100 ℃时， 由于水蒸汽的最大压力（饱和压力）ps > p，故 v,max s p p p    1） v s p p  v v v gv 1 p v R T    s s s gv 1 p v R T    2）    此时 v v v,max p p p p   

10 三、含湿量d 一1kg干空气中所含水蒸气的质量d= mv m d=P,' =P= =0.622P=0.622 Pa Pa Pa P-P =0.622 p,≈0.622 kg水蒸气/kg干空气kg/kgDA 卫-p、 讨论： a)当p一定时， d←→p, b)pp一定，t个→卫个→d个升温吸湿原理 上游充通大学 Mar/14,2017 10 SHANGHAI JLAO TONG UNIVERSITY

Mar/14, 2017 10 10 三、含湿量d ——1kg干空气中所含水蒸气的质量 v a m d m  a）当p一定时， v d p  t  v 0.622 p p  s    p d s s p p p     0.622 v v 0.622 p p p   v a V d V    v a    v g,v a g,a p R T p R T  v a 0.622 p p  kg水蒸气/kg干空气 b) p、 一定， 升温吸湿原理 kg/kgDA 讨论：

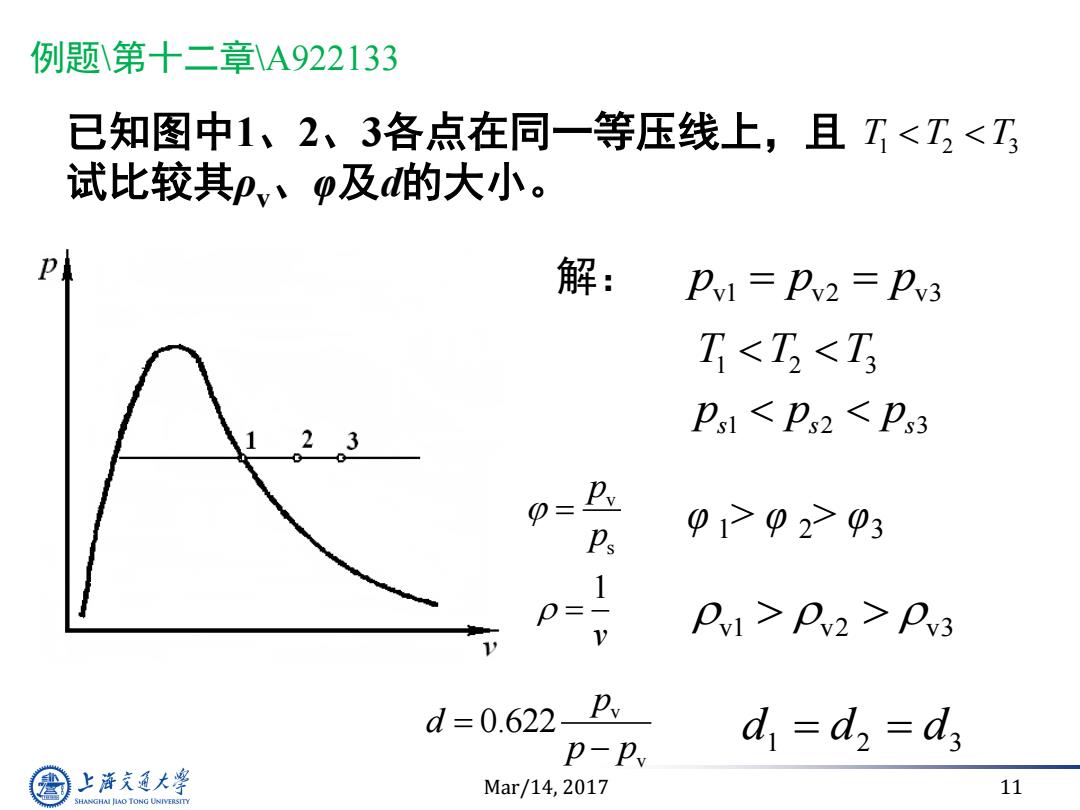
例题1第十二章\A922133 已知图中1、2、3各点在同一等压线上，且T02>03 1 P Pv2>Pv3 d=0.622 d =d,d; p-P 上游充通大学 Mar/14,2017 11 SHANGHAI JLAO TONG UNIVERSITY

Mar/14, 2017 11 已知图中1、2、3各点在同一等压线上，且 试比较其ρv、φ及d的大小。 解： v1 v2 v3 p p p   T T T 1 2 3   s s s 1 2 3 p p p      v1 v2 v3   d1  d2  d3 φ 1> φ 2> φ3 T T T 1 2 3   v s p p   1 v   v v 0.622 p d p p   例题\第十二章\A922133