
电机学课堂讲义第三部分同步电机16h 上海交通大学电气工程系EE SJTU 第六讲同步电机负载运行原理 重点:电磁关系,时空矢量图,等效电路 难点:电枢反应电势 问题:同步电机带负载运行的电磁过程如何描述?同步电抗如何定义?如何描述同步电机的等效电 路?同步发电机有哪些运行特性? 5、独立负载运行 (1)同步发电机 同步电机在原动机拖动下,以同步速旋转,转子加励磁电压,电枢接阻抗负载的运行方式 同步电机电磁耦合模型 同步电机直轴与交轴气隙可能不同,因此直轴与交轴电枢反应不同,需要将直轴和交轴分开考虑电 路和磁路的耦合作用。由于磁场感应的电势总是滞后磁场90°,且同步发电机的直轴正方向超前交轴 正方向90°,因此直轴磁场产生的感应电势正好位于交轴正方向,而交轴磁场产生的感应电势在直轴 反方向,即出现负号。根据电枢磁场等价的方式,将定子三相绕组用等效的两相d与q正交绕组取 代,空间产生的电枢磁势不变。 三相对称绕组流过对称电流产生的合成磁势基波幅值等于每相磁势最大值的m/2倍 m 4 Wks1 2π2p 2 m.ph (1)静止两相正交绕组(等效匝数等于每相等效匝数的m/2倍,交流电流有效值不变) F =F cos(ot-0)=F cosotcos0+F cos(cott/2)cos(0-/2) (2)同步旋转两相正交绕组(等效匝数等于每相等效匝数的血/2倍,直流电流等于每相电流幅值) F=F cos(at-0)=F cos(ot F cos(ot-0,)cosu -F sin(ot-0 )sinu 个A相轴线 4个d相轴线 R wN U. NΦ q相轴线 ⊕ 8X -wN④ U B B相轴线 C相轴线 电枢电流时兖矢量I滞后于q轴中角,那么电枢磁势时空矢量F与电流I重合,电枢磁势可以看成是两 个正交磁势F和F的合成,或者等价地电枢电流时空矢量Ia可以分解为两个正交矢量I和I的合成。 直轴主磁路包含转子直轴磁阻Rrd、直轴气隙磁阻Rsd、定子铁芯磁阻Rs,直轴转子励磁磁势F、直轴 电枢反应磁势Fad=NiIa相互作用,同时考虑转子励磁漏磁阻Rt.和电枢漏磁路磁阻Rs。 交轴主磁路包含转子交轴磁阻Ra、交轴气隙磁阻Ra、定子铁芯磁阻Rs,交轴转子没有励磁磁势, 只有交轴电枢反应磁势F=NI的作用,同时不考虑转子交轴漏磁阻,但考虑电枢漏磁路磁阻。 交轴电压方程等效电路:交轴电流I,在电枢电阻R。上的压降、直轴电枢漏磁通Φs如在交轴感应电枢漏 电势wN1Φsod、直轴气隙磁通Φa在电枢绕组感应交轴电势ωN1Φd(包括交轴电枢反应电势owN1Φa和交 轴励磁电势wNΦr两者的合成)
电机学课堂讲义 第三部分 同步电机 16h 上海交通大学电气工程系 EE SJTU 1 第六讲 同步电机负载运行原理 重点:电磁关系,时空矢量图,等效电路 难点:电枢反应电势 问题:同步电机带负载运行的电磁过程如何描述?同步电抗如何定义?如何描述同步电机的等效电 路?同步发电机有哪些运行特性? 5、独立负载运行 (1)同步发电机 同步电机在原动机拖动下,以同步速旋转,转子加励磁电压,电枢接阻抗负载的运行方式。 同步电机电磁耦合模型 同步电机直轴与交轴气隙可能不同,因此直轴与交轴电枢反应不同,需要将直轴和交轴分开考虑电 路和磁路的耦合作用。由于磁场感应的电势总是滞后磁场90 0 ,且同步发电机的直轴正方向超前交轴 正方向90 0 ,因此直轴磁场产生的感应电势正好位于交轴正方向,而交轴磁场产生的感应电势在直轴 反方向,即出现负号。根据电枢磁场等价的方式,将定子三相绕组用等效的两相d与q正交绕组取 代,空间产生的电枢磁势不变。 三相对称绕组流过对称电流产生的合成磁势基波幅值等于每相磁势最大值的m/2倍 m m ph w m F m I p m W k F , 1 1 2 2 4 2 = = ! (1)静止两相正交绕组(等效匝数等于每相等效匝数的m/2倍,交流电流有效值不变) F = F cos(#t $" ) = F cos#t cos" + F cos(#t $ ! / 2)cos(" $ ! / 2) a m m m (2)同步旋转两相正交绕组(等效匝数等于每相等效匝数的m/2倍,直流电流等于每相电流幅值) a m m r a m r a m r a F = F cos(#t $" ) = F cos(#t $" +! ) = F cos(#t $" )cos! $ F sin(#t $" )sin! 电枢电流时空矢量Ia滞后于q轴ψ角,那么电枢磁势时空矢量Fa与电流Ia重合,电枢磁势可以看成是两 个正交磁势Fad和Faq的合成,或者等价地电枢电流时空矢量Ia可以分解为两个正交矢量Id和Iq的合成。 直轴主磁路包含转子直轴磁阻Rmrd、直轴气隙磁阻Rmδd、定子铁芯磁阻Rms,直轴转子励磁磁势Ff、直轴 电枢反应磁势Fad=N1Id相互作用,同时考虑转子励磁漏磁阻Rmfσ和电枢漏磁路磁阻Rmsσ。 交轴主磁路包含转子交轴磁阻Rmrq、交轴气隙磁阻Rmδq、定子铁芯磁阻Rms,交轴转子没有励磁磁势, 只有交轴电枢反应磁势Faq=N1Iq的作用,同时不考虑转子交轴漏磁阻,但考虑电枢漏磁路磁阻。 交轴电压方程等效电路:交轴电流Iq在电枢电阻Ra上的压降、直轴电枢漏磁通Φsσd在交轴感应电枢漏 电势ωN1Φsσd、直轴气隙磁通Φδd在电枢绕组感应交轴电势ωN1Φδd(包括交轴电枢反应电势ωN1Φad和交 轴励磁电势ωN1Φaf两者的合成)。 A相轴线 S N Z B A Y C X B相轴线 C相轴线 Id Iq d相轴线 S N Ud Uq q相轴线 Uq I Ra q ωN1Φsσd ωN1Φδd Ud I Ra d -ωN1Φsσq -ωN1Φδq Φδd Rmδd Ff Fad Rmfσ Rmsσ Φfσ Φsσd Rms Rmrd Φδq Rmδq Rmrq Rmsσ Faq Φsσq Rms

电机学课堂讲义第三部分同步电机16h 上海交通大学电气工程系EE SJTU 值得注意的是相同励磁绕组磁势与电枢磁势在气隙中产生的基波磁密(磁通)是不同的,为了解决 这个问题,需要对电枢磁势进行折算,使得折算后的电枢磁势与励磁磁势等价,从而可以利用磁路 计算磁通。折算的原则是产生相同基波气隙磁密所需的励磁磁势与电枢磁势关系。由于直轴与交轴 磁路不同,因此折算时,电枢磁势的直轴和交轴分量都按照直轴位置产生的磁密进行折算? 直轴电压方程等效电路:直轴电流I在电枢电阻R。上的压降、交轴电枢漏磁通Φs在直轴感应电枢漏 电势-wN1④sa、交轴气隙磁通Φ在电枢绕组感应直轴电枢反应电势-wN1④a。 空间坐标参考为转子直轴,称为d轴,滞后直轴90°电角的转子坐标位置称为交轴或q轴。 凸极同步电机转子励磁绕组是集中绕组,产生基波励磁磁场依靠不均匀气隙: 隐极同步电机转子励磁绕组是分布绕组,气隙是均匀的,能产生较好的基波励磁磁场。 电枢绕组产生的气隙磁势波形与气隙形状没有关系,仅仅取决于电流分布。 隐极同步电机气隙均匀,直轴和交轴气隙磁阻一样,直轴和交轴的转子磁阻在忽略转子饱和的条件 下也认为一样(其实存在大小齿有一点区别)。这样线性磁路隐极同步电机电磁耦合模型可以合并 成时空矢量耦合模型。 重要结论:在电枢电压确定的条件下,气隙磁场每极磁通幅值基本不变!因为电枢电流在电枢电阻 和漏电抗上的压降基本上可以忽略不计。 稳态等效电路:(1)合成气隙磁场产生的电势,漏阻抗压降,端电压构成回路,获得电枢电流,交 流电机: (2)隐极同步发电机:合成气隙磁场产生的电势包含两部分,转子励磁绕组基波气隙磁场产生的励 磁电势和电枢反应电流引起的基波气隙磁场产生的电枢反应电势,后者可以用电枢反应电抗压降形 式表示。 (3)凸极同步发电机:需要采用双反应理论,分别建立直轴与交轴等效电路。 (4)直轴电流为零的交轴等效电路:直流电机。 A、基本电磁关系: 负载运行时同步发电机的机电能量转换过程比较复杂,可以表述为以下反馈过程: 励磁电压→励磁电流→励磁磁势→主磁场一基波主磁密→主磁通→励磁电势→端电压→负载电流: 负载电流就是电枢电流,它有三个作用:产生电枢反应(AR)磁场,包括直轴和交轴电枢反应磁 场,形成直轴和交轴电枢反应电势:产生电枢漏磁场,形成漏电势:引起电枢绕组电阻压降。这三 个作用反过来影响电枢端电压与负载电流,最终达到动态平衡,稳定运行,如图1所示。 0 Uf→y→F>By→Bn→④E→U。→l=La 9 Fa) →Fad→Bad→Bad→Φad→Ead Fag→Bag→Bag1→Φag→Eag →Bao→Φao→E。 >Rala 0 lad Fad 图1同步发电机负载运行时的电磁关系 图2时空矢量Fa,I分解 电枢电流→AR磁势→直轴AR磁势→直轴AR磁场→直轴AR基波磁密→直轴AR基波电势: 卜--→交轴AR磁势→交轴AR磁场→交轴AR基波磁密→交轴AR基波电势: 电枢电流→漏磁场→漏电势:电枢电流→电阻压降。 B、电势与电流的关系 2
电机学课堂讲义 第三部分 同步电机 16h 上海交通大学电气工程系 EE SJTU 2 值得注意的是相同励磁绕组磁势与电枢磁势在气隙中产生的基波磁密(磁通)是不同的,为了解决 这个问题,需要对电枢磁势进行折算,使得折算后的电枢磁势与励磁磁势等价,从而可以利用磁路 计算磁通。折算的原则是产生相同基波气隙磁密所需的励磁磁势与电枢磁势关系。由于直轴与交轴 磁路不同,因此折算时,电枢磁势的直轴和交轴分量都按照直轴位置产生的磁密进行折算? 直轴电压方程等效电路:直轴电流Id在电枢电阻Ra上的压降、交轴电枢漏磁通Φsσq在直轴感应电枢漏 电势-ωN1Φsσq、交轴气隙磁通Φδq在电枢绕组感应直轴电枢反应电势-ωN1Φδq。 空间坐标参考为转子直轴,称为d轴,滞后直轴90 0 电角的转子坐标位置称为交轴或q轴。 凸极同步电机转子励磁绕组是集中绕组,产生基波励磁磁场依靠不均匀气隙; 隐极同步电机转子励磁绕组是分布绕组,气隙是均匀的,能产生较好的基波励磁磁场。 电枢绕组产生的气隙磁势波形与气隙形状没有关系,仅仅取决于电流分布。 隐极同步电机气隙均匀,直轴和交轴气隙磁阻一样,直轴和交轴的转子磁阻在忽略转子饱和的条件 下也认为一样(其实存在大小齿有一点区别)。这样线性磁路隐极同步电机电磁耦合模型可以合并 成时空矢量耦合模型。 重要结论:在电枢电压确定的条件下,气隙磁场每极磁通幅值基本不变!因为电枢电流在电枢电阻 和漏电抗上的压降基本上可以忽略不计。 稳态等效电路:(1)合成气隙磁场产生的电势,漏阻抗压降,端电压构成回路,获得电枢电流,交 流电机; (2)隐极同步发电机:合成气隙磁场产生的电势包含两部分,转子励磁绕组基波气隙磁场产生的励 磁电势和电枢反应电流引起的基波气隙磁场产生的电枢反应电势,后者可以用电枢反应电抗压降形 式表示。 (3)凸极同步发电机:需要采用双反应理论,分别建立直轴与交轴等效电路。 (4)直轴电流为零的交轴等效电路:直流电机。 A、基本电磁关系: 负载运行时同步发电机的机电能量转换过程比较复杂,可以表述为以下反馈过程: 励磁电压→励磁电流→励磁磁势→主磁场→基波主磁密→主磁通→励磁电势→端电压→负载电流; 负载电流就是电枢电流,它有三个作用:产生电枢反应(AR)磁场,包括直轴和交轴电枢反应磁 场,形成直轴和交轴电枢反应电势;产生电枢漏磁场,形成漏电势;引起电枢绕组电阻压降。这三 个作用反过来影响电枢端电压与负载电流,最终达到动态平衡,稳定运行,如图1所示。 电枢电流→AR磁势→直轴AR磁势→直轴AR磁场→直轴AR基波磁密→直轴AR基波电势; |----→交轴AR磁势→交轴AR磁场→交轴AR基波磁密→交轴AR基波电势; 电枢电流→漏磁场→漏电势;电枢电流→电阻压降。 B、电势与电流的关系 Uf If Ff Bf Bf1 Φf Ef Ua IL=Ia Ia Fa Fad Bad Bad1 Φad Ead Faq Baq Baq1 Φaq Eaq RaIa Baσ Φaσ Eσ 图1 同步发电机负载运行时的电磁关系 图2 时空矢量Fa, Ia分解 0 q d Fa (Ia) ψ ωt Iad Fad Iaq Faq

电机学课堂讲义第三部分同步电机16h 上海交通大学电气工程系EE SJTU 由于电枢电流空间分布与其产生的气隙磁势空间分布都与电机气隙大小无关,两者是线性关系。而 时空矢量可以看成是不同的正交分解的两个时空矢量之和,因此将电枢电流或磁势时空矢量分解成 直轴和交轴分量是合理的,也是正确的,如图2所示。分析同步电机的双反应理论就是基于这一时空 矢量分解思想。 直轴与交轴电枢反应电势是由相应的直轴和交轴电枢反应磁场产生的。在磁路不饱和的线性条件 下,直轴电枢反应电势与直轴电枢反应磁密呈正比,而磁密与直轴电枢反应磁势或电流呈正比,因 此直轴电枢反应电势与直轴电枢反应电流分量呈正比。 同样地,交轴电枢反应电势也与交轴电枢电流呈正比。 利用直轴和交轴等效气隙磁导得到直轴和交轴基波磁通(磁链)与电枢电流分量之间的关系 od =aFd =aW lad Vod =WKAaWilad =32pAaWilad Ladlad ④g1=÷A,Fg=2A,W1am,平g1=2Wk1A,W1g=22pA,W1g=Loglog 其中,Ld,Lag分别为直轴和交轴电枢反应电感,这些结果与前面通过气隙磁场能量法得到的每相电 感不同。直轴和交轴电枢电流分量前采用系数32,这是由于图15中合成磁势所对应的是每相电流幅 值产生的等效磁势的3/2倍,而系数4/π是由于每相等效集中绕组W,匝引起的每极磁通幅值。磁链是 2p个极的总磁链,等于每极磁链乘以极数。 于是,直轴和交轴电枢反应电势分别为 Ead =Ladlad =Xadlad Eag =@Laglag =Xaglag 其中,Xa和Xag分别为直轴和交轴电枢反应电抗。 根据正方向规定如图3所示,对于发电机电流由发电机流向负载产生电压降 落,电流、电势与磁通符合右手螺旋关系。这样,电势的相位滞后于产生该电 势的磁场90电角度,因此直轴和交轴电枢反应电势时空矢量的相位分别滞后 于直轴和交轴电枢反应磁势或电流90电角度,即可以用时空矢量(复数)表 示为 图3正方向惯例 B..--jol-xjol 电枢漏电势是由漏磁场产生的,引入等效漏磁导及相应的漏电感和漏电抗,用电枢电流表示电枢绕 组的每极等效漏磁通、总漏磁链和漏电势分别为 Φo=÷Ao月=W1.,平。=2pAW1。=L1, E。=-jLLa-jXL 励磁电势与励磁电流的关系由空载特性确定,励磁电势时空矢量的相位滞后于直轴(轴)正方向 90°电角度。需要强调的是采用了双反应理论和引入等效磁导概念后,将原来电枢绕组的三相电磁耦 合状态进行了解耦,即等效后的三相电枢系统不再存在电磁耦合作用,成为独立的或时空统一的三 相绕组。从电感参数来说,漏电感包括自漏电感和两相互漏电感,直轴和交轴电枢反应电感也是三 相合成磁场的作用结果。 C、电势平衡关系 根据正方向惯例和基尔霍夫电压定律(KVL),可以写出电势平衡关系 Et+Ead Eaa+Ea-R la-Ua=0 3
电机学课堂讲义 第三部分 同步电机 16h 上海交通大学电气工程系 EE SJTU 3 由于电枢电流空间分布与其产生的气隙磁势空间分布都与电机气隙大小无关,两者是线性关系。而 时空矢量可以看成是不同的正交分解的两个时空矢量之和,因此将电枢电流或磁势时空矢量分解成 直轴和交轴分量是合理的,也是正确的,如图2所示。分析同步电机的双反应理论就是基于这一时空 矢量分解思想。 直轴与交轴电枢反应电势是由相应的直轴和交轴电枢反应磁场产生的。在磁路不饱和的线性条件 下,直轴电枢反应电势与直轴电枢反应磁密呈正比,而磁密与直轴电枢反应磁势或电流呈正比,因 此直轴电枢反应电势与直轴电枢反应电流分量呈正比。 同样地,交轴电枢反应电势也与交轴电枢电流呈正比。 利用直轴和交轴等效气隙磁导得到直轴和交轴基波磁通(磁链)与电枢电流分量之间的关系 ! "ad1 = 4 # $dFad = 3 2 4 # $dW1Iad , ! "ad1 = 3 2 4 # Wkw1$dW1Iad = 3 2 2p$dW1 2 Iad = Lad Iad ! "aq1 = 4 # $qFaq = 3 2 4 # $qW1Iaq , ! "aq1 = 3 2 4 # Wkw1$qW1Iaq = 3 2 2 p$qW1 2 Iaq = Laq Iaq 其中,Lad,Laq分别为直轴和交轴电枢反应电感,这些结果与前面通过气隙磁场能量法得到的每相电 感不同。直轴和交轴电枢电流分量前采用系数3/2,这是由于图15中合成磁势所对应的是每相电流幅 值产生的等效磁势的3/2倍,而系数4/π是由于每相等效集中绕组W1匝引起的每极磁通幅值。磁链是 2p个极的总磁链,等于每极磁链乘以极数。 于是,直轴和交轴电枢反应电势分别为 ! Ead ="Lad Iad = Xad Iad , ! Eaq ="Laq Iaq = Xaq Iaq 其中,Xad和Xaq分别为直轴和交轴电枢反应电抗。 根据正方向规定如图3所示,对于发电机电流由发电机流向负载产生电压降 落,电流、电势与磁通符合右手螺旋关系。这样,电势的相位滞后于产生该电 势的磁场900 电角度,因此直轴和交轴电枢反应电势时空矢量的相位分别滞后 于直轴和交轴电枢反应磁势或电流900 电角度,即可以用时空矢量(复数)表 示为 ! Ead = " j#Lad Iad = " jXad Iad , ! Eaq = " j#Laq Iaq = " jXaq Iaq 电枢漏电势是由漏磁场产生的,引入等效漏磁导及相应的漏电感和漏电抗,用电枢电流表示电枢绕 组的每极等效漏磁通、总漏磁链和漏电势分别为 ! "a# = 4 $ %#Fa = 4 $ %#W1Ia , ! "a# = 2p$#W1 2 Ia = L# Ia , ! E" = # j$L" Ia = # jX" Ia 励磁电势与励磁电流的关系由空载特性确定,励磁电势时空矢量的相位滞后于直轴(d轴)正方向 900 电角度。需要强调的是采用了双反应理论和引入等效磁导概念后,将原来电枢绕组的三相电磁耦 合状态进行了解耦,即等效后的三相电枢系统不再存在电磁耦合作用,成为独立的或时空统一的三 相绕组。从电感参数来说,漏电感包括自漏电感和两相互漏电感,直轴和交轴电枢反应电感也是三 相合成磁场的作用结果。 C、电势平衡关系 根据正方向惯例和基尔霍夫电压定律(KVL),可以写出电势平衡关系 ! Ef + Ead + Eaq + E" # Ra Ia # Ua = 0 图3 正方向惯例 Ia Φ Ua E
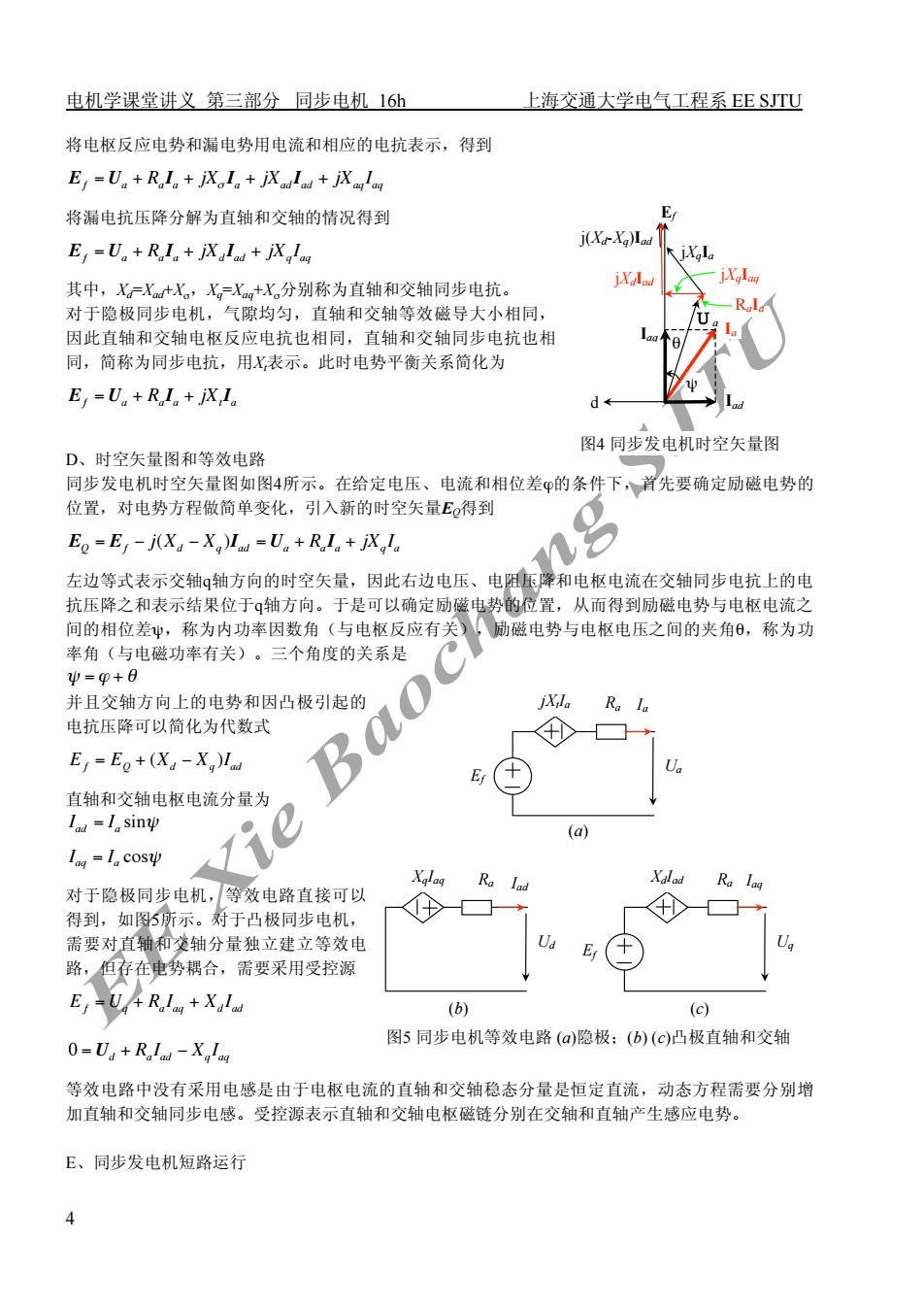
电机学课堂讲义第三部分同步电机16h 上海交通大学电气工程系EE SJTU 将电枢反应电势和漏电势用电流和相应的电抗表示,得到 Ej=U。+R。Ln+jX。La+jXadIad+jXaqIag 将漏电抗压降分解为直轴和交轴的情况得到 E=U。+RLn+jXla+jXalag j(Xa-Xg)Iad 其中,X-Xad+X。,X,Xag+X.分别称为直轴和交轴同步电抗。 iXalad 对于隐极同步电机,气隙均匀,直轴和交轴等效磁导大小相同, 因此直轴和交轴电枢反应电抗也相同,直轴和交轴同步电抗也相 同,简称为同步电抗,用X表示。此时电势平衡关系简化为 E=Un+RI。+jXLa d 图4同步发电机时空矢量图 D、时空矢量图和等效电路 同步发电机时空矢量图如图4所示。在给定电压、电流和相位差的条件下,首先要确定励磁电势的 位置,对电势方程做简单变化,引入新的时空矢量E得到 Eo=E,-jX4-X,La=U。+RL。+jX,La 左边等式表示交轴q轴方向的时空矢量,因此右边电压、电阻压降和电枢电流在交轴同步电抗上的电 抗压降之和表示结果位于q轴方向。于是可以确定励磁电势的位置,从而得到励磁电势与电枢电流之 间的相位差ψ,称为内功率因数角(与电枢反应有关)励磁电势与电枢电压之间的夹角,称为功 率角(与电磁功率有关)。三个角度的关系是 ψ=p+8 并且交轴方向上的电势和因凸极引起的 Ra la 电抗压降可以简化为代数式 E=Eo+(Xa-X)lad U 直轴和交轴电枢电流分量为 Iad=I sinψ (a) 1g=L,cosψ Xglag Ra lad Xalad Ra lag 对于隐极同步电机,等效电路直接可以 得到,如图5所示。对于凸极同步电机, 需要对直轴和交轴分量独立建立等效电 路,但存在电势耦合,需要采用受控源 Ef-U+Ralag Xalad (b) (c) 图5同步电机等效电路(α)隐极:(b)(c)凸极直轴和交轴 0=U4+R。1a-Xg1ag 等效电路中没有采用电感是由于电枢电流的直轴和交轴稳态分量是恒定直流,动态方程需要分别增 加直轴和交轴同步电感。受控源表示直轴和交轴电枢磁链分别在交轴和直轴产生感应电势。 E、同步发电机短路运行 4
电机学课堂讲义 第三部分 同步电机 16h 上海交通大学电气工程系 EE SJTU 4 将电枢反应电势和漏电势用电流和相应的电抗表示,得到 ! Ef = Ua + Ra Ia + jX" Ia + jXad Iad + jXaq Iaq 将漏电抗压降分解为直轴和交轴的情况得到 ! Ef = Ua + Ra Ia + jXd Iad + jXq Iaq 其中,Xd=Xad+Xσ,Xq=Xaq+Xσ分别称为直轴和交轴同步电抗。 对于隐极同步电机,气隙均匀,直轴和交轴等效磁导大小相同, 因此直轴和交轴电枢反应电抗也相同,直轴和交轴同步电抗也相 同,简称为同步电抗,用Xt表示。此时电势平衡关系简化为 ! Ef = Ua + Ra Ia + jXt Ia D、时空矢量图和等效电路 同步发电机时空矢量图如图4所示。在给定电压、电流和相位差ϕ的条件下,首先要确定励磁电势的 位置,对电势方程做简单变化,引入新的时空矢量EQ得到 ! EQ = Ef " j(Xd " Xq )Iad = Ua + Ra Ia + jXq Ia 左边等式表示交轴q轴方向的时空矢量,因此右边电压、电阻压降和电枢电流在交轴同步电抗上的电 抗压降之和表示结果位于q轴方向。于是可以确定励磁电势的位置,从而得到励磁电势与电枢电流之 间的相位差ψ,称为内功率因数角(与电枢反应有关),励磁电势与电枢电压之间的夹角θ,称为功 率角(与电磁功率有关)。三个角度的关系是 ! " = # + $ 并且交轴方向上的电势和因凸极引起的 电抗压降可以简化为代数式 ! E f = EQ + (Xd " Xq )Iad 直轴和交轴电枢电流分量为 ! Iad = Ia sin" ! Iaq = Ia cos" 对于隐极同步电机,等效电路直接可以 得到,如图5所示。对于凸极同步电机, 需要对直轴和交轴分量独立建立等效电 路,但存在电势耦合,需要采用受控源 ! E f = Uq + Ra Iaq + Xd Iad ! 0 = Ud + Ra Iad " Xq Iaq 等效电路中没有采用电感是由于电枢电流的直轴和交轴稳态分量是恒定直流,动态方程需要分别增 加直轴和交轴同步电感。受控源表示直轴和交轴电枢磁链分别在交轴和直轴产生感应电势。 E、同步发电机短路运行 图4 同步发电机时空矢量图 d Ia ψ θ jXdIad Iad Ef Iaq Ua jXqIaq jXqIa j(Xd-Xq)Iad RaIa XqIaq Ra Ud Iad Ef XdIad Ra Uq Iaq Ef jXtIa Ra Ua Ia (c) 图5 同步电机等效电路 (a)隐极;(b) (c)凸极直轴和交轴 (b) (a)

电机学课堂讲义第三部分同步电机16h 上海交通大学电气工程系EE SJTU 同步发电机电枢绕组三相短路,输出电压等于零,U。=0,直轴和交轴电枢电压分量都等于零。在忽 略电枢电阻的条件下,根据直轴与交轴等效电路和电压方程可以发现,交轴电枢反应电流分量也等 于零,只有直轴电枢反应电流分量,即短路电流I=ld,直轴电枢反应起去磁作用,以抵消励磁磁 场。励磁电势与电枢反应电势平衡E=Xalk。 因电枢反应起去磁作用,因此磁路不饱和,励磁电势或励磁电流与电枢电流成线性关系,电枢短路 电流随励磁电流变化的短路特性是过零点的线性直线,并且直轴不饱和同步电抗X=EIk。 F、零功率因数负载运行 假设负载功率因数等于零,那么电枢电压可以用电枢电流和电抗表示 Ua=iXLIa:Ud=-XLIag:Ua=XLIad 代入直轴和交轴电压方程得到 E=R I +(Xd+X)Iod =(Xd +XL)Iad O=R Iad (Xa+X)Ia=-(Xa +XL)Iag 于是,在忽略电枢电阻的条件下,交轴电枢反应电流分量等于零,当负载电抗与直轴同步电抗之和 为感性时,直轴电枢反应起去磁作用:当负载电抗与直轴同步电抗之和为容性时,直轴电枢反应起 助磁作用:当负载电抗与直轴同步电抗之和接近零时,电枢电阻不能忽略,或者励磁电流接近零, 否则电枢电流因串联谐振而损坏绕组。 G.直轴电枢反应电流等于零条件下的同步电机 当1=0时,电枢电流只有交轴电枢反应电流分量, 忽略电枢电阻,直轴电枢电压分量等于电枢电流与 交轴同步电抗乘积,交轴电枢电压分量等于励磁电势,因此额定负载功率因数与励磁电势标么值 E1-cosey1-X 电枢电流超前电压,功率角与功率因数角大小相等。 (2)同步电动机 同步电机转子通过辅助装置拖动到同步速,电枢与三相对称电源连接,转子加励磁电流,因此可以 驱动机械负载或直流发电机运行。关于同步电机起动过程略。这时,电枢电流方向与同步发电机相 反,因此电枢反应磁场以及由此感应的电枢反应电势方向也改变,但电压和励磁电势的方向不变, 电压平衡关系成为 U。=月+R+jXla+X,g 同步电动机稳态等效电路与同步发电机一样。 6、标幺值系统 标么值是实际值与基值之比。基值通常选取额定值。采用标么值的优势是: 数值归一化,额定值的标么值等于1,其它采用有效值和相量表示的数值都小于1: 等效电路和基本方程不再需要折算: 不同容量的同类电机具有相同或相近的标么值参数,性能比较接近: 不同坐标系之间的变换矩阵不变: 5
电机学课堂讲义 第三部分 同步电机 16h 上海交通大学电气工程系 EE SJTU 5 同步发电机电枢绕组三相短路,输出电压等于零,Ua=0,直轴和交轴电枢电压分量都等于零。在忽 略电枢电阻的条件下,根据直轴与交轴等效电路和电压方程可以发现,交轴电枢反应电流分量也等 于零,只有直轴电枢反应电流分量,即短路电流Iak=Iad,直轴电枢反应起去磁作用,以抵消励磁磁 场。励磁电势与电枢反应电势平衡Ef=XdIak。 因电枢反应起去磁作用,因此磁路不饱和,励磁电势或励磁电流与电枢电流成线性关系,电枢短路 电流随励磁电流变化的短路特性是过零点的线性直线,并且直轴不饱和同步电抗Xd=Ef/Iak。 F、零功率因数负载运行 假设负载功率因数等于零,那么电枢电压可以用电枢电流和电抗表示 ! Ua = jXL Ia , ! Ud = "XL Iaq , ! Uq = XL Iad 代入直轴和交轴电压方程得到 ! E f = Ra Iaq + (Xd + XL )Iad " (Xd + XL )Iad ! 0 = Ra Iad " (Xq + XL )Iaq # "(Xq + XL )Iaq 于是,在忽略电枢电阻的条件下,交轴电枢反应电流分量等于零;当负载电抗与直轴同步电抗之和 为感性时,直轴电枢反应起去磁作用;当负载电抗与直轴同步电抗之和为容性时,直轴电枢反应起 助磁作用;当负载电抗与直轴同步电抗之和接近零时,电枢电阻不能忽略,或者励磁电流接近零, 否则电枢电流因串联谐振而损坏绕组。 G.直轴电枢反应电流等于零条件下的同步电机 当Id=0时,电枢电流只有交轴电枢反应电流分量,忽略电枢电阻,直轴电枢电压分量等于电枢电流与 交轴同步电抗乘积,交轴电枢电压分量等于励磁电势,因此额定负载功率因数与励磁电势标幺值 ! E f * = cos" N = 1# Xq *2 电枢电流超前电压,功率角与功率因数角大小相等。 (2)同步电动机 同步电机转子通过辅助装置拖动到同步速,电枢与三相对称电源连接,转子加励磁电流,因此可以 驱动机械负载或直流发电机运行。关于同步电机起动过程略。这时,电枢电流方向与同步发电机相 反,因此电枢反应磁场以及由此感应的电枢反应电势方向也改变,但电压和励磁电势的方向不变, 电压平衡关系成为 ! Ua = Ef + Ra Ia + jXd Iad + jXq Iaq 同步电动机稳态等效电路与同步发电机一样。 6、标幺值系统 标幺值是实际值与基值之比。基值通常选取额定值。采用标幺值的优势是: 数值归一化,额定值的标幺值等于1,其它采用有效值和相量表示的数值都小于1; 等效电路和基本方程不再需要折算; 不同容量的同类电机具有相同或相近的标幺值参数,性能比较接近; 不同坐标系之间的变换矩阵不变;

电机学课堂讲义第三部分同步电机16h 上海交通大学电气工程系EE SJTU 有些物理量的标么值相同,如电感与额定频率的电抗,磁通与磁链,电流与磁势等: 瞬时值、有效值、相量或时空矢量的基值相同: 交流电机标么值功率与相数无关: 同类电机的特性曲线具有相似的形式: 总结: 同步电机是定转子同时独立励磁的。从定子观测磁场是时间交变空间分布的同步旋转波:从转子观 测磁场是静止恒定的分布波。同步电机在同步坐标系中观测时空矢量是恒定的矢量,可以采用简单 的复数量或直流量进行代数运算。基本方程、时空矢量图和等效电路是分析电机的三大法宝。电枢 反应的性质主要是交轴交磁作用、直轴去磁或助磁作用,它与电机的运行状态内功率因数角有关。 功率角与电磁功率有关,将在以后介绍。 教学方法 两个独立磁场一一内部电磁关系一一电枢电压平衡一一相量图/时空矢量图 等效电路及其参 数—标么值系统。 EE Xie Baochang 6
电机学课堂讲义 第三部分 同步电机 16h 上海交通大学电气工程系 EE SJTU 6 有些物理量的标幺值相同,如电感与额定频率的电抗,磁通与磁链,电流与磁势等; 瞬时值、有效值、相量或时空矢量的基值相同; 交流电机标幺值功率与相数无关; 同类电机的特性曲线具有相似的形式; 总结: 同步电机是定转子同时独立励磁的。从定子观测磁场是时间交变空间分布的同步旋转波;从转子观 测磁场是静止恒定的分布波。同步电机在同步坐标系中观测时空矢量是恒定的矢量,可以采用简单 的复数量或直流量进行代数运算。基本方程、时空矢量图和等效电路是分析电机的三大法宝。电枢 反应的性质主要是交轴交磁作用、直轴去磁或助磁作用,它与电机的运行状态内功率因数角有关。 功率角与电磁功率有关,将在以后介绍。 教学方法 两个独立磁场——内部电磁关系——电枢电压平衡——相量图/时空矢量图——等效电路及其参 数——标幺值系统

电机学课堂进义第八部分卓越工程师课程 上海交通大学电气工程系EE SJTU 附录:同步发电机时空矢量图 正方向规定同步发电机是电源,发电机电枢外接负载。对于负载正电压产生正电流,对于发电机绕 组正电流产生正磁通,正磁通产生正电势。转子以逆时针旋转为正,直轴与转子励磁磁场N极一致, 交轴滞后直轴90°电角,三相绕组轴线作为各自的时轴,以便获得多时轴单矢量的表达效果。 根据转子励磁电流产生的励磁磁势时空矢量,励磁磁势不仅在转子绕组产生漏磁场与漏磁通,而且 还与电枢耦合的主磁场与主磁通,主磁通在电枢绕组感应励磁电势。假设励磁每极磁通幅值中,转 子直轴超前A相绕组轴线0电角度,那么A相绕组励磁磁通瞬时值为 中A=Φmcos日, 考虑到磁通与磁链的关系,A相绕组产生的励磁电势瞬时值根据电磁感应定律得到 dundun de, =o,WkwΦmsin6, dt de,dt 或者用励磁电势幅值表示为 eA=Eicos(6,-π/2) 由此可见,A相绕组励磁电势滞后于直轴90°电角,位于交轴,即励磁电势的时空矢量位于交轴。 由于电枢回路呈现感性,因此同步发电机接对称负载时通常产生滞后的对称电枢电流。电流滞后励 磁电势的相位角用中表示。一旦电枢电流形成,将产生三相合成旋转磁势时空矢量,合成电枢磁势的 位置与电流时空矢量一致。对于凸极同步发电机,直轴与校轴气隙长度不同,电枢磁势与其产生的 磁场不是简单的比例关系,而是需要利用双反应理论,分别确定直轴与交轴电枢反应磁势所产生的 电枢反应磁场。假设合成电枢磁势基波以A相轴线为参考的表达式为 fn=Fcos(ω,t-) 其中幅值F位于=w1t。它可以分解为直轴与交轴两个分量 F=F cos(t-0,).F =F cos(o+) 从电枢上观测,是两个幅值分别为F和Fg,且分别处在转子直轴和交轴的旋转磁势 fa fad fag 9 其中,两个旋转磁势的表达式分别为 KE fad F cos(@t-0,)cos(0,-0) Ead fm=Fcos(,t-6,+π/2)cos(0,-π12-8) U 根据前面分析得到转子位置角日,=ω,t+型+π/2。 Fag la 8 1 F 尽管电枢友应磁势仍然是基波,但是产生的电枢反应磁场中除了基 波还有谐波。对于基波磁场与磁通,将在电枢绕组中感应电枢反应 ψ 电势。这些电势将滞后于相应的磁通90°电角。电枢电流还产生漏磁 d← lad Fad 场和漏磁通,同样要感应漏电势,电枢绕组有电阻,电枢绕组电阻附图同步发电机时空矢量图 压降与电流同相位。 从转子上观测时空矢量图中各时空矢量是静止的,但从电枢上观测它们以转子电角频率旋转。所 以,同步电机模型都是建立在转子q坐标系统基础上的。 电机是机电耦合系统,内部本质上是电磁耦合系统。 7
电机学课堂讲义 第八部分 卓越工程师课程 上海交通大学电气工程系 EE SJTU 7 附录:同步发电机时空矢量图 正方向规定同步发电机是电源,发电机电枢外接负载。对于负载正电压产生正电流,对于发电机绕 组正电流产生正磁通,正磁通产生正电势。转子以逆时针旋转为正,直轴与转子励磁磁场N极一致, 交轴滞后直轴900 电角,三相绕组轴线作为各自的时轴,以便获得多时轴单矢量的表达效果。 根据转子励磁电流产生的励磁磁势时空矢量,励磁磁势不仅在转子绕组产生漏磁场与漏磁通,而且 还与电枢耦合的主磁场与主磁通,主磁通在电枢绕组感应励磁电势。假设励磁每极磁通幅值Φfm,转 子直轴超前A相绕组轴线θr电角度,那么A相绕组励磁磁通瞬时值为 ! " fA = #fm cos$r 考虑到磁通与磁链的关系,A相绕组产生的励磁电势瞬时值根据电磁感应定律得到 ! efA = " d# fA dt = " d# fA d$r d$r dt =%1 Wkw1&fm sin$r 或者用励磁电势幅值表示为 ! efA = E fm cos("r # $ /2) 由此可见,A相绕组励磁电势滞后于直轴900 电角,位于交轴,即励磁电势的时空矢量位于交轴。 由于电枢回路呈现感性,因此同步发电机接对称负载时通常产生滞后的对称电枢电流。电流滞后励 磁电势的相位角用ψ表示。一旦电枢电流形成,将产生三相合成旋转磁势时空矢量,合成电枢磁势的 位置与电流时空矢量一致。对于凸极同步发电机,直轴与交轴气隙长度不同,电枢磁势与其产生的 磁场不是简单的比例关系,而是需要利用双反应理论,分别确定直轴与交轴电枢反应磁势所产生的 电枢反应磁场。假设合成电枢磁势基波以A相轴线为参考的表达式为 ! fa = Fa cos("1t #$) 其中幅值Fa位于θ=ω1t。它可以分解为直轴与交轴两个分量 ! Fad = Fa cos("1t #$r), ! Faq = Fa cos("1t #$r + % /2) 从电枢上观测,是两个幅值分别为Fad和Faq,且分别处在转子直轴和交轴的旋转磁势 ! fa = f ad + f aq 其中,两个旋转磁势的表达式分别为 ! fad = Fa cos("1t #$r)cos($r #$) ! faq = Fa cos("1t #$r + % /2)cos($r # % /2 #$) 根据前面分析得到转子位置角 ! "r =#1t +$ + % /2。 尽管电枢反应磁势仍然是基波,但是产生的电枢反应磁场中除了基 波还有谐波。对于基波磁场与磁通,将在电枢绕组中感应电枢反应 电势。这些电势将滞后于相应的磁通900 电角。电枢电流还产生漏磁 场和漏磁通,同样要感应漏电势,电枢绕组有电阻,电枢绕组电阻 压降与电流同相位。 从转子上观测时空矢量图中各时空矢量是静止的,但从电枢上观测它们以转子电角频率旋转。所 以,同步电机模型都是建立在转子dq坐标系统基础上的。 电机是机电耦合系统,内部本质上是电磁耦合系统。 附图 同步发电机时空矢量图 d Ia ψ θ Ead Iad Ef Iaq Ua Eaq q RaIa Ff Fa Eaσ Faq Fad A q d Bf θr EfA

先假设磁路是线性的,忽略磁路饱和的影响,所有电磁参数都是确定的常数,可以采用叠加原理。 分析时将气隙磁场基波与谐波分开,气隙磁场中由电枢绕组产生的谐波归于漏磁场,转子磁极绕组 产生的谐波忽略不计(否则计算电枢谐波电势),电枢绕组中的感应电势由总漏磁场和总气隙基波 磁场决定,气隙磁场在同步电机中将励磁磁极产生的、电枢磁势直轴分量与交轴分量产生的分别考 虑,再用叠加原理合成。 不考虑磁滞与涡流,如何考虑铁芯损耗? 磁路模型与电机结构密切相关,但是旋转电机的基本结构是定子、转子和两者之间的气隙。定转子 铁芯通常包含齿与磁轭,他们是使得气隙磁通连续的主磁路。根据磁路半周期对称性,磁势采用每 极磁势,主磁路为同时耦合定转子绕组的封闭磁力线对称回路长度的一半,包括一个气隙,定子一 个齿和半极距定子磁轭,转子一个齿和半极距转子磁轭,各部分磁阻根据相应磁路长度、电枢轴向 有效长度和不同圆周半径位置半极距大小,即由电机的几何尺寸进行计算。漏磁路比较复杂,必须 根据实际绕组分布及电流计算所有漏磁路磁通,以及与绕组匝链的磁链,再获得等效漏磁通与相应 的磁阻。漏磁路磁阻可以认为是恒定的,因为磁感应线主要经过相对磁导率接近空气的槽部或端部 闭合。主磁路中气隙磁阻也是恒定的,但主磁路中铁芯部分磁阻(定转子齿或磁轭磁阻)呈非线 性,因为铁磁材料的磁化曲线存在饱和。整个主磁路的B-H磁化特性可以等效为磁通与磁势的关系曲 线,因为正弦波气隙磁密幅值与每极磁通幅值的关系可以表示为平均磁密与每极电枢表面积乘积: Φ。=2Bnm6Iet/π。 每极磁势等于平均磁场强度与磁路长度的乘积F。=HLm 电气模型:电枢绕组采用三相集中等效绕组,只考虑基波气隙磁势和基波气隙磁场的作用,电枢绕 组产生的谐波磁场作为漏磁场的一部分,与槽漏磁、 端部漏磁一起统称为漏磁场。从磁场的角度, 分析各绕组中的电势,电流产生的磁势和磁场。 规定正方向:用线圈表示!两种常用方法:发电机惯例(同步电机),电动机惯例(异步电机), 两种惯例混合使用(变压器)。不变的是电流与磁链,磁链与感应电势的正方向总是符合右手螺旋 关系。 按照发电机惯例,电流在负载上形成端电压:按照电动机惯例,电压在电枢绕组上形成正电流。 稳态运行时,幅值与有效值比例关系恒定,幅值等于有效值的根号2倍,因此在时空矢量图表示同步 电机电磁关系时,只要采用相同的量就没有区别,即都用有效值或者都是幅值,在列方程计算时, 则习惯上采用有效值。(采用有效值可能比较习惯) 第一个问题:三相时间对称量的时空矢量表示(电流、电压、电势): 通常采用三角函数表示,三角函数又可以表示为复矢量,复矢量在复平面上的表示,在同一复平面 上,三相对称时间函数对应的复矢量空间互差120°,即单时轴多矢量的表示方法。三相不对称正弦 函数可以利用对称分量法分解为正、负和零相序,其中正相序相位依次滞后120°、负相序相位依次 超前20°,而零相序相位一致。如果采用多时轴的方法又会怎样呢?假设将每相时轴与各相绕组的 相轴致,而各相相轴按照正相序逆时针互差120°排列,那么三相复矢量在空间就重合,即多时轴 单矢量表示方法。 第二个问题:电流时空矢量与电流产生的合成磁势时空矢量的关系: 如果按照电流与其产生的磁通满足右手螺旋关系,磁通与其产生的电势也满足右手螺旋关系,那么 三相对称绕组流过对称电流产生的空间合成磁势时空矢量与电流矢量是重合的,合成磁势与其产生 的磁通密度在气隙均匀的情况下是重合的,磁通密度与绕组轴线重合时产生的磁通或磁链最大,电 势矢量滞后于产生该电势的磁通矢量90°。 第三个问题:转子正弦波磁场在定子三相绕组中产生的感应电势时空矢量表示: 8
8 先假设磁路是线性的,忽略磁路饱和的影响,所有电磁参数都是确定的常数,可以采用叠加原理。 分析时将气隙磁场基波与谐波分开,气隙磁场中由电枢绕组产生的谐波归于漏磁场,转子磁极绕组 产生的谐波忽略不计(否则计算电枢谐波电势),电枢绕组中的感应电势由总漏磁场和总气隙基波 磁场决定,气隙磁场在同步电机中将励磁磁极产生的、电枢磁势直轴分量与交轴分量产生的分别考 虑,再用叠加原理合成。 不考虑磁滞与涡流,如何考虑铁芯损耗? 磁路模型与电机结构密切相关,但是旋转电机的基本结构是定子、转子和两者之间的气隙。定转子 铁芯通常包含齿与磁轭,他们是使得气隙磁通连续的主磁路。根据磁路半周期对称性,磁势采用每 极磁势,主磁路为同时耦合定转子绕组的封闭磁力线对称回路长度的一半,包括一个气隙,定子一 个齿和半极距定子磁轭,转子一个齿和半极距转子磁轭,各部分磁阻根据相应磁路长度、电枢轴向 有效长度和不同圆周半径位置半极距大小,即由电机的几何尺寸进行计算。漏磁路比较复杂,必须 根据实际绕组分布及电流计算所有漏磁路磁通,以及与绕组匝链的磁链,再获得等效漏磁通与相应 的磁阻。漏磁路磁阻可以认为是恒定的,因为磁感应线主要经过相对磁导率接近空气的槽部或端部 闭合。主磁路中气隙磁阻也是恒定的,但主磁路中铁芯部分磁阻(定转子齿或磁轭磁阻)呈非线 性,因为铁磁材料的磁化曲线存在饱和。整个主磁路的B-H磁化特性可以等效为磁通与磁势的关系曲 线,因为正弦波气隙磁密幅值与每极磁通幅值的关系可以表示为平均磁密与每极电枢表面积乘积: $# = 2Bm#lfe " /! 。 每极磁势等于平均磁场强度与磁路长度的乘积 Fa = HavLmc 。 电气模型:电枢绕组采用三相集中等效绕组,只考虑基波气隙磁势和基波气隙磁场的作用,电枢绕 组产生的谐波磁场作为漏磁场的一部分,与槽漏磁、端部漏磁一起统称为漏磁场。从磁场的角度, 分析各绕组中的电势,电流产生的磁势和磁场。 规定正方向:用线圈表示!两种常用方法:发电机惯例(同步电机),电动机惯例(异步电机), 两种惯例混合使用(变压器)。不变的是电流与磁链,磁链与感应电势的正方向总是符合右手螺旋 关系。 按照发电机惯例,电流在负载上形成端电压;按照电动机惯例,电压在电枢绕组上形成正电流。 稳态运行时,幅值与有效值比例关系恒定,幅值等于有效值的根号2倍,因此在时空矢量图表示同步 电机电磁关系时,只要采用相同的量就没有区别,即都用有效值或者都是幅值,在列方程计算时, 则习惯上采用有效值。(采用有效值可能比较习惯) 第一个问题:三相时间对称量的时空矢量表示(电流、电压、电势); 通常采用三角函数表示,三角函数又可以表示为复矢量,复矢量在复平面上的表示,在同一复平面 上,三相对称时间函数对应的复矢量空间互差1200 ,即单时轴多矢量的表示方法。三相不对称正弦 函数可以利用对称分量法分解为正、负和零相序,其中正相序相位依次滞后120 0 、负相序相位依次 超前120 0 ,而零相序相位一致。如果采用多时轴的方法又会怎样呢?假设将每相时轴与各相绕组的 相轴一致,而各相相轴按照正相序逆时针互差1200 排列,那么三相复矢量在空间就重合,即多时轴 单矢量表示方法。 第二个问题:电流时空矢量与电流产生的合成磁势时空矢量的关系; 如果按照电流与其产生的磁通满足右手螺旋关系,磁通与其产生的电势也满足右手螺旋关系,那么 三相对称绕组流过对称电流产生的空间合成磁势时空矢量与电流矢量是重合的,合成磁势与其产生 的磁通密度在气隙均匀的情况下是重合的,磁通密度与绕组轴线重合时产生的磁通或磁链最大,电 势矢量滞后于产生该电势的磁通矢量90 0 。 第三个问题:转子正弦波磁场在定子三相绕组中产生的感应电势时空矢量表示;

电机学课堂进义第八部分卓越工程师课程 上海交通大学电气工程系EE SJTU 转子磁场位于直轴正方向,每极磁通确定,在每相绕组中的等效磁通与磁链等于每极磁通在绕组轴 线(相轴)上的投影(磁链还要乘以等效串联匝数),根据电磁感应定律,感应励磁电势瞬时值等 于磁链对时间的微分的相反数,因此感应励磁电势的相位总是滞后于励磁磁通90°电角,对于同步发 电机来说励磁电势总是位于交轴正方向。 第四个问题:电枢电流产生的两个空间位置正交(轴与q轴)的正弦波磁场分别在电枢绕组中产生 的感应电势时空矢量(凸极同步电机的双反应理论): 一般物理意义上,电势与产生电势的磁场励磁电流关系 E=-jo =-jo,N=-jo,NAF =-jo AN'I=-jo LI =-jXI 根据电磁感应定律的正弦矢量表示,磁链等于匝数与磁通乘积,磁通等于磁导与磁势乘积,磁势等 于匝数与电流乘积,磁导与匝数平方乘积表示电感,角频率与电感乘积表示电抗,电势与电抗压降 相差一个符号。 电枢电流产生的合成基波磁势不一定正好与直轴或交轴重合,因此电枢电流产生的气隙磁场需要根 据双反应理论计算,即将合成基波磁势分解成直轴与交轴电枢反应磁势基波分量,相应地电枢电流 也可以分解成直轴和交轴电枢反应电流分量,假设电枢电流滞后于交轴一个电角度,那么双反应理 论的数学描述为 尽管直轴和交轴电枢反应磁势是基波分量,但是产生的磁通密度是否也是不含谐波的基波分量呢? 直轴电枢反应磁势基波分量的幅值与转子励磁电流产生相同磁势幅值引起的直轴磁通密度是否一 致?要回答这些问题,必须要根据直轴和交轴位置的气隙大小分布和励磁绕组情况才能确定。 转子每极励磁电流产生的励磁磁势波形与励磁绕组分布和磁极形状有关,(凸极与隐极),励磁磁 势产生的磁通密度也与直轴气隙大小和极弧形状有关,其每极磁通与基波磁通密度关系 直轴电枢反应磁势基波分量产生的磁通密度分布,每极磁通,磁通密度的基波分量 通常将电枢反应磁势的直轴与交轴分量折算到等效的励磁磁势,用折算系数来表示 直轴电枢反应磁势的折算系数是产生相同直轴磁通密度基波幅值条件下,等效励磁磁势幅值与直轴 电枢反应磁势基波分量幅值之比。 交轴电枢反应磁势的折算系数是在交轴电枢反应磁势产生相同直轴磁通密度基波幅值条件下,等效 励磁磁势幅值与交轴电枢反应磁势基波分量幅值之比。 第五个问题:电枢电流时空矢量的漏磁场在电枢绕组中产生的感应电势: 电枢电流产生的漏磁场在电枢绕组中的交变频率等于电枢电流频率,磁场大小与电枢电流呈正比, 因此漏磁通与电枢电流星正比,其产生的感应电势(漏电势)大小与电流呈正比,相位滞后于电流 90°。 电势是驱动正电荷运动的方向,它与相应的电抗压降方向相反。 第六个问题:电枢电流时空矢量在电枢绕组电阻上的电压降落用时空矢量表示。 电枢电流在绕组电阻上的电压降与电流呈正比,因此两者方向一致。 电枢电流产生的气隙磁场谐波性质与磁极电流产生的谐波磁场性质比较,列表 v次谐波 电枢磁场谐波 励磁磁场谐波 频率 电流频率f1 vf 极对数 vp vp 转速 n/v 转子转速n1 削弱方法 分布、短距和斜槽 分布,极弧形状 9
电机学课堂讲义 第八部分 卓越工程师课程 上海交通大学电气工程系 EE SJTU 9 转子磁场位于直轴正方向,每极磁通确定,在每相绕组中的等效磁通与磁链等于每极磁通在绕组轴 线(相轴)上的投影(磁链还要乘以等效串联匝数),根据电磁感应定律,感应励磁电势瞬时值等 于磁链对时间的微分的相反数,因此感应励磁电势的相位总是滞后于励磁磁通90 0 电角,对于同步发 电机来说励磁电势总是位于交轴正方向。 第四个问题:电枢电流产生的两个空间位置正交(d轴与q轴)的正弦波磁场分别在电枢绕组中产生 的感应电势时空矢量(凸极同步电机的双反应理论); 一般物理意义上,电势与产生电势的磁场励磁电流关系 ! E = " j#1$ = " j#1N% = " j#1N&F = " j#1&N2 I = " j#1LI = " jXI 根据电磁感应定律的正弦矢量表示,磁链等于匝数与磁通乘积,磁通等于磁导与磁势乘积,磁势等 于匝数与电流乘积,磁导与匝数平方乘积表示电感,角频率与电感乘积表示电抗,电势与电抗压降 相差一个符号。 电枢电流产生的合成基波磁势不一定正好与直轴或交轴重合,因此电枢电流产生的气隙磁场需要根 据双反应理论计算,即将合成基波磁势分解成直轴与交轴电枢反应磁势基波分量,相应地电枢电流 也可以分解成直轴和交轴电枢反应电流分量,假设电枢电流滞后于交轴一个电角度,那么双反应理 论的数学描述为 尽管直轴和交轴电枢反应磁势是基波分量,但是产生的磁通密度是否也是不含谐波的基波分量呢? 直轴电枢反应磁势基波分量的幅值与转子励磁电流产生相同磁势幅值引起的直轴磁通密度是否一 致?要回答这些问题,必须要根据直轴和交轴位置的气隙大小分布和励磁绕组情况才能确定。 转子每极励磁电流产生的励磁磁势波形与励磁绕组分布和磁极形状有关,(凸极与隐极),励磁磁 势产生的磁通密度也与直轴气隙大小和极弧形状有关,其每极磁通与基波磁通密度关系 直轴电枢反应磁势基波分量产生的磁通密度分布,每极磁通,磁通密度的基波分量 通常将电枢反应磁势的直轴与交轴分量折算到等效的励磁磁势,用折算系数来表示 直轴电枢反应磁势的折算系数是产生相同直轴磁通密度基波幅值条件下,等效励磁磁势幅值与直轴 电枢反应磁势基波分量幅值之比。 交轴电枢反应磁势的折算系数是在交轴电枢反应磁势产生相同直轴磁通密度基波幅值条件下,等效 励磁磁势幅值与交轴电枢反应磁势基波分量幅值之比。 第五个问题:电枢电流时空矢量的漏磁场在电枢绕组中产生的感应电势; 电枢电流产生的漏磁场在电枢绕组中的交变频率等于电枢电流频率,磁场大小与电枢电流呈正比, 因此漏磁通与电枢电流呈正比,其产生的感应电势(漏电势)大小与电流呈正比,相位滞后于电流 90 0 。 电势是驱动正电荷运动的方向,它与相应的电抗压降方向相反。 第六个问题:电枢电流时空矢量在电枢绕组电阻上的电压降落用时空矢量表示。 电枢电流在绕组电阻上的电压降与电流呈正比,因此两者方向一致。 电枢电流产生的气隙磁场谐波性质与磁极电流产生的谐波磁场性质比较,列表 ν次谐波 电枢磁场谐波 励磁磁场谐波 频率 电流频率f1 νf1 极对数 νp νp 转速 n1/ν 转子转速n1 削弱方法 分布、短距和斜槽 分布,极弧形状