上海交通大学：《电机学 Electric Machinery》课程教学资源（PPT讲稿）交流电机共性问题（电势）

饮水思 源爱国 电机学 荣校 厚德载 2010卓越工程师班 物 自 上海交通大学电气工程系 强不息

饮水思源爱国荣校 厚德载物自强不息 电机学 2010卓越工程师班 上海交通大学电气工程系

交流电机共性问题：电势 水思 ·电势的概念 ·电势的波图形 源爱国 荣 ·电势的基波和谐波分量 校 厚 电势的串联 德 载 电枢磁场感应电势的特点 物 ·磁极磁场感应电势的特点 自 强 不 息 2022-3-12 上海交通大学电气工程系谢宝昌 2

饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 2 交流电机共性问题：电势 • 电势的概念 • 电势的波图形 • 电势的基波和谐波分量 • 电势的串联 • 电枢磁场感应电势的特点 • 磁极磁场感应电势的特点

饮 电势的概念 水 电势是电枢绕组在时变磁场引起的涡旋电场在串联线圈中的累积描述，是时 思 间的函数，不是空间的函数，但不同空间位置绕组的感应电势不同。交流电 源 枢绕组的电势具有如下特点： (1)规定电势与磁场的参考方向符合右手螺旋关系； 爱 这一点主要是为了满足电磁感应定律和楞次定律。 国 (2)绕组的电势等于各并联支路的电势； 荣 这一点是为了满足空载无环流的要求。 (3)并联支路的电势等于各串联线圈电势的代数和； 校 厚 这一点是必须遵循基尔霍夫电压定律。 (4)线圈的电势等于线圈内各导体电势的代数和； 德 (5)电势的基波与谐波含量取决于磁链（各线圈磁通代数和）的基波和谐波 载 含量。 物 需要注意的是，尽管实际电机绕组是安放在铁芯槽内的，但是在计算电势时 自 等价于导体集中在电枢表面槽口处，这样电势只与槽口位置气隙磁场有关。 在分析电势时，不关心绕组实际串并联连接方式，计算时考虑到对称性，都 强 认为是串联，所得结果除以并联支路数。这里电势主要与气隙磁场相关联， 不 不考虑漏磁场感应的漏电势。 息 2022-3-12 上海交通大学电气工程系谢宝昌 3

饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 3 电势的概念 电势是电枢绕组在时变磁场引起的涡旋电场在串联线圈中的累积描述，是时 间的函数，不是空间的函数，但不同空间位置绕组的感应电势不同。交流电 枢绕组的电势具有如下特点： （1）规定电势与磁场的参考方向符合右手螺旋关系； 这一点主要是为了满足电磁感应定律和楞次定律。 （2）绕组的电势等于各并联支路的电势； 这一点是为了满足空载无环流的要求。 （3）并联支路的电势等于各串联线圈电势的代数和； 这一点是必须遵循基尔霍夫电压定律。 （4）线圈的电势等于线圈内各导体电势的代数和； （5）电势的基波与谐波含量取决于磁链（各线圈磁通代数和）的基波和谐波 含量。 需要注意的是，尽管实际电机绕组是安放在铁芯槽内的，但是在计算电势时 等价于导体集中在电枢表面槽口处，这样电势只与槽口位置气隙磁场有关。 在分析电势时，不关心绕组实际串并联连接方式，计算时考虑到对称性，都 认为是串联，所得结果除以并联支路数。这里电势主要与气隙磁场相关联， 不考虑漏磁场感应的漏电势

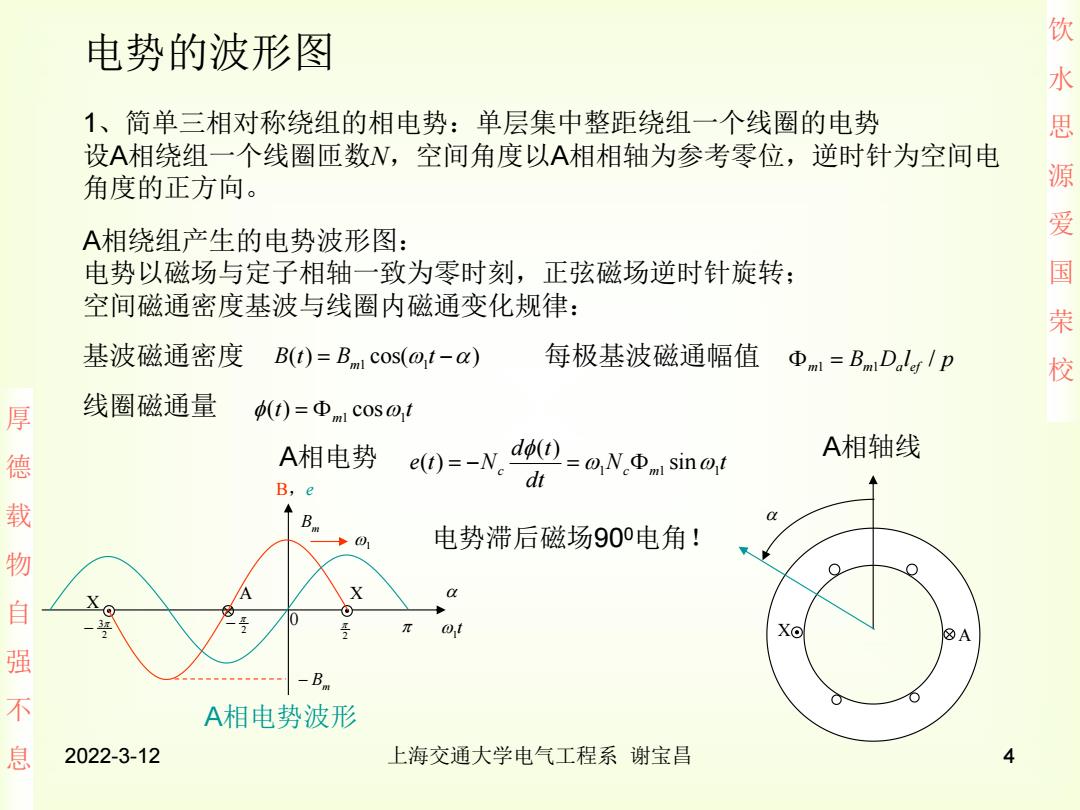
饮 电势的波形图 水 1、简单三相对称绕组的相电势：单层集中整距绕组一个线圈的电势 思 设A相绕组一个线圈匝数N,空间角度以A相相轴为参考零位，逆时针为空间电 角度的正方向。 源 A相绕组产生的电势波形图： 爱 电势以磁场与定子相轴一致为零时刻，正弦磁场逆时针旋转； 国 空间磁通密度基波与线圈内磁通变化规律： 荣 基波磁通密度B(t)=Bnm1cos(o,t-) 每极基波磁通幅值 Φml=BmD.lerI p 校 厚 线圈磁通量 (t)=Φm1cos0,t A相电势 e()=-N.d dp=o,N.Φsint A相轴线 德 载 B,e 01 电势滞后磁场90°电角！ 物 自强 X 0 π wt X⊙ A -B 不 A相电势波形 息 2022-3-12 上海交通大学电气工程系谢宝昌 4

饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 4 电势的波形图 1、简单三相对称绕组的相电势：单层集中整距绕组一个线圈的电势 设A相绕组一个线圈匝数N，空间角度以A相相轴为参考零位，逆时针为空间电 角度的正方向。 A相绕组产生的电势波形图： 电势以磁场与定子相轴一致为零时刻，正弦磁场逆时针旋转； 空间磁通密度基波与线圈内磁通变化规律： X A A相轴线  A相电势波形 ( ) cos( ) B t  Bm1 1 t  t t m1 1 ( )   cos B D l p m m a ef /  1  1 A相电势 N t dt d t e t Nc 1 c m1 1 sin ( ) ( )        B，e  0 2 3  2  2 Bm  Bm A X X 1  t 1 电势滞后磁场900电角！ 基波磁通密度 每极基波磁通幅值 线圈磁通量

电势的波形图 水 空间磁通密度谐波与线圈内磁通变化规律： 思 (1)磁极谐波磁场：转速等于基波，极数等于基波的谐波次数倍 源 B,(t)=Bv cos(v@,t-va) 中(t)=ΦCOS(vo,t) Φmv=Bmv Dalet vp 爱 A相电势 国 e,)=-N.项@=o,N.Φsinvod 电势滞后磁场900电角！ 荣 dt (2)电枢谐波磁势磁场：谐波频率等于基波，极数等于基波的谐波次数倍 校 厚 B.(t)=B cos(@t-va) 中(t)=ΦcoS(ot) Φmv=BmvDaler /vp 德 载 A相电势 物 .(-xd-on 电势滞后磁场900电角！ 自 A相电势波形：磁极磁场基波和电枢磁势磁场都感应基波电势，磁极谐波磁场感 强 应谐波电势；谐波电势大小与谐波磁通密度幅值成正比。 下面仅讨论磁极磁场产生的电枢电势。 不 息 2022-3-12 上海交通大学电气工程系谢宝昌 5

饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 5 电势的波形图 空间磁通密度谐波与线圈内磁通变化规律： （1）磁极谐波磁场：转速等于基波，极数等于基波的谐波次数倍 A相电势波形：磁极磁场基波和电枢磁势磁场都感应基波电势，磁极谐波磁场感 应谐波电势；谐波电势大小与谐波磁通密度幅值成正比。 下面仅讨论磁极磁场产生的电枢电势。 ( ) cos( ) B t  Bm 1 t  ( ) cos( ) 1 t t   m  B D l p m  m a ef / A相电势 N t dt d t e t Nc 1 c m 1 sin ( ) ( )           （2）电枢谐波磁势磁场：谐波频率等于基波，极数等于基波的谐波次数倍 ( ) cos( ) B t  Bm 1 t  ( ) cos( ) 1 t t   m  B D l p m  m a ef / A相电势 N t dt d t e t Nc 1 c m 1 sin ( ) ( )           电势滞后磁场900电角！ 电势滞后磁场900电角！

饮 电势的波形图 水 2、双层整数槽集中短距绕组一相每对极两个线圈的电势 思 设A相绕组每对极两个线圈，每个线圈匝数N,空间角度以A相相轴为参考零位， 源 逆时针为空间电角度的正方向。短距线圈节距系数 B=ylr 爱 A相绕组产生的电势波形图 (1)短距线圈AX和A2X2串联；磁通密度给定，线圈AX1和X2A2的磁通量计算： 国 荣 B(t)=B cos(@t-a) )DB cos(@-@da=sin(Bz/2)coso 校 Φm1=Bm1Dlr/p 厚 DBos-a)daim(/2yco 德 e=-N de0+N.4出 d40=2a,N.Φnk1 sin A相轴线 电势基波 _dt 载 Bπ/2 B,e 基波短距系数k,=sin(Bm/2) 物 电势滞后磁场90电角！ 自 Xi X2 A2 AL a AT A 强 -π -B 0 @t 不 A相两个线圈合成电势波形 息 2022-3-12 上海交通大学电气工程系谢宝昌 6

饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 6 电势的波形图 2、双层整数槽集中短距绕组一相每对极两个线圈的电势 设A相绕组每对极两个线圈，每个线圈匝数Nc，空间角度以A相相轴为参考零位， 逆时针为空间电角度的正方向。短距线圈节距系数 A相绕组产生的电势波形图 （1）短距线圈A1X1和A2X2串联；磁通密度给定，线圈A1X1和X2A2的磁通量计算： A相两个线圈合成电势波形   y / ( ) cos( ) B t  Bm1 1 t  B D l p m m a ef /  1  1 t D l B t d t a ef m m1 1 / 2 / 2 2 1 1 1 1  ( ) cos( )  sin( / 2) cos         t D l B t d t a ef m m1 1 / 2 / 2 2 1 1 1 2  ( ) cos( )  sin( / 2) cos            N k t dt d t N dt d t e Nc c 1 c m1 y1 1 1 2 2 sin ( ) ( )          B，e t 1 0 2   2   Bm  Bm A1 X1 X2 A2 A1 电势滞后磁场900电角！ 电势基波   1 A1 X1 A相轴线  A2 X2  / 2 基波短距系数 sin( / 2) ky1  

电势的波形图 水思 A相绕组产生的电势波形图 (2)将短距线圈AX1和A2X2串联看成是整距线圈AX2和A2X1串联。 磁通密度给定，两等价线圈的磁通量计算 磁通密度 B(t)=B cos(@t-a) 源爱国 荣 线圈AX2的磁通量 42(t)=Φm1cos(o,t-π/2+Bm/2) 厚 线圈X2A的磁通量 421(t)=-Φmc0s(o,t+π/2-Bm/2) A相轴线 德 每极磁通量幅值 Φm1=Bnm1 alerI p βπ/2 载 物 电势 )2.,sio e=-N.di 自 X2 基波短距系数k,=sin(Bm/2) A 强 不 两种方法计算结果完全相同 息 2022-3-12 上海交通大学电气工程系谢宝昌 7

饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 7 电势的波形图 A相绕组产生的电势波形图 （2）将短距线圈A1X1和A2X2串联看成是整距线圈A1X2和A2X1串联。 磁通密度给定，两等价线圈的磁通量计算 两种方法计算结果完全相同 ( ) cos( ) B t  Bm1 1 t  B D l p m m a ef /  1  1 ( ) cos( / 2 / 2) 12 t  m1 1 t    N k t dt d t N dt d t e Nc c 1 c m1 y1 1 12 21 2 sin ( ) ( )          ( ) cos( / 2 / 2) 21 t  m1 1 t    A1 X1 A相轴线  A2 X2  / 2 磁通密度 线圈A1X2的磁通量 线圈X2A1的磁通量 每极磁通量幅值 电势 基波短距系数 sin( / 2) ky1  

饮 电势的波形图 水 3、双层整数槽分布短距绕组一相每对极2q个线圈的电势 思 设A相绕组每对极2q个线圈，每个线圈匝数N,空间角度以A相相轴为参考零位， 源 顺时针为空间电角度的正方向。短距线圈节距系数 B=ylr A相绕组产生的电势波形图： 爱 (1)2q个短距线圈A1.aX1.g和A2X2a'看成是q个分布的短距线圈对。 国 如每极9槽，线圈节距y=8,q=3的电势波形为 荣 校 厚 e A相轴线 Bm/2+(q-1)a./2 德 载 A2.4 88gw 88。 图风段 物 A14 X2 亦A1.g @t B号 24 --A1 自 ⑧ A29 强 A相2q个线圈合成磁势波形 不 息 2022-3-12 上海交通大学电气工程系谢宝昌 8

饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 8 电势的波形图 3、双层整数槽分布短距绕组一相每对极2q个线圈的电势 设A相绕组每对极2q个线圈，每个线圈匝数Nc，空间角度以A相相轴为参考零位， 顺时针为空间电角度的正方向。短距线圈节距系数 A相绕组产生的电势波形图： （1）2q个短距线圈A1.qX1.q和A2.qX2.q，看成是q个分布的短距线圈对。 如每极9槽，线圈节距y=8，q=3的电势波形为 A相2q个线圈合成磁势波形   y / B，e  2   2  Bm  Bm A1.q X1.q A相轴线  A2.q X2.q / 2 ( 1) / 2 e   q   t 1 0 A  1.q A2.q X1.q A2.q X2.q A1.q

电势的波形图 饮 磁通密度 B(t)=B cos(@t-a) 思 线圈对A,X1和AzX2的磁通量 4(t)=2Φm1kcos(o,t-(g-1)a./2) 其它线圈对的磁通量 源爱国 4(t)=2④nmik,1cos(o,t+(k-1)a。-(g-1)a。/2) 每极磁通量幅值Φnm1=Bm1D1gIp 荣 电势基波 磁链 e=-N.() 台dt 校 0=N24d 厚 k=1 du(t) 德 -2N.Dmk,>cos(@l+(k-1)a.-(q-1)a./2) dt =2oqNΦmikw1sino,t 载 -2N..k, 基波绕组系数 kyn kyka 物 自 -2No.kRewwa 基波短距系数k,=sin(Bm/2) 强 -2N0,ga7 sin(qa。/2 cos(@,t) 不 基波分布系数k-sin(qa/2 gsin(a./2) 息 2022-3-12 上海交通大学电气工程系谢宝昌 9

饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 9 ( ) cos( ) B t  Bm1 1 t  B D l p m m a ef /  1  1 ( ) 2 cos( ( 1) / 2) 1 m1 y1 1 q e  t   k  t    qN k t dt d t dt d t e N c m w q k k c 1 1 1 1 1 2 sin ( ) ( )            磁通密度 线圈对A1X1 和A2X2的磁通量 其它线圈对的磁通量 每极磁通量幅值 电势基波 电势的波形图 ( ) 2 cos( ( 1) ( 1) / 2) k m1 y1 1 e q e  t   k  t  k      磁链 cos( ) sin( / 2) sin( / 2) 2 1 1 2 Re 2 Re 2 cos( ( 1) ( 1) / 2) ( ) ( ) 1 1 1 ( ( 1) / 2) 1 1 1 ( ( 1) ( 1) / 2) 1 1 1 1 1 1 1 1 1 t q N k e e N k e N k e N k t k q t N t e e c m y j jq j t q c m y q k j t k q c m y q k c m y e e q k c k e e e e e                                                       基波绕组系数 w1 y1 q1 k  k k 基波短距系数 sin( / 2) ky1   基波分布系数 sin( / 2) sin( / 2) 1 e e q q q k   

饮 电势的波形图 水 思 对于整数槽绕组来说，每相每对极下各线圈电势代数和的基波分量是相同的。 电势的基波是以基波频率周期变化的正弦波。 源 每相电势基波等于上述计算结果乘以极对数再除以并联支路数，根据并联支路数 爱 计算每相串联匝数 国 相电势 @.pqNDmksinot=0Wk.msinot e= 总是滞后磁场90电角 荣 校 双层整数槽绕组的每相串联匝数 W=2pqNe 厚 a 德 双层整数槽绕组的每相电势幅值Em1=o,WM中ml 载 复杂的整数槽绕组的电势基波由简单三相绕组的一相电势基波计算方法获得双层 物 短距、分布绕组的合成电势基波，并引入短距系数和分布系数，它们在磁势计算 中已经出现过；也可以利用空间复矢量计算电势基波合成幅值，而不考虑相位， 自 因为电势基波的相位总是滞后磁场90电角； 强 这样，将复杂的积分和三角函数求和运算转变成简单的复矢量和运算。 不 息 2022-3-12 上海交通大学电气工程系谢宝昌 10

饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 10 电势的波形图 对于整数槽绕组来说，每相每对极下各线圈电势代数和的基波分量是相同的。 电势的基波是以基波频率周期变化的正弦波。 每相电势基波等于上述计算结果乘以极对数再除以并联支路数，根据并联支路数 计算每相串联匝数 复杂的整数槽绕组的电势基波由简单三相绕组的一相电势基波计算方法获得双层 短距、分布绕组的合成电势基波，并引入短距系数和分布系数，它们在磁势计算 中已经出现过；也可以利用空间复矢量计算电势基波合成幅值，而不考虑相位， 因为电势基波的相位总是滞后磁场900电角； 这样，将复杂的积分和三角函数求和运算转变成简单的复矢量和运算。 t Wk t a pqN k e w m c m w 1 1 1 1 1 1 1 1 sin sin 2         a pqN W 2 c  相电势 双层整数槽绕组的每相串联匝数 总是滞后磁场900电角 m1 1W w1 m1 双层整数槽绕组的每相电势幅值 E  k 