
饮水思 源爱国 电机学 荣校 厚德载 2010卓越工程师班 物 自 上海交通大学电气工程系 强不息
饮水思源爱国荣校 厚德载物自强不息 电机学 2010卓越工程师班 上海交通大学电气工程系

交流电机共性问题:磁势 水思 ·磁势的概念 ·磁势的波图形 源爱国 荣 ·磁势波中的基波和谐波 校 厚 ·磁势波的合成 德 载 合成磁势基波和谐波的特点 物 ·磁势波产生的磁场 自 强 不 息 2022-3-12 上海交通大学电气工程系谢宝昌 2
饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 2 交流电机共性问题:磁势 • 磁势的概念 • 磁势的波图形 • 磁势波中的基波和谐波 • 磁势波的合成 • 合成磁势基波和谐波的特点 • 磁势波产生的磁场

饮 磁势的概念 水 磁势是电枢表面电流空间分布的累积描述,既是电流时间变化的函数,又是 思 空间位置的函数。交流电枢绕组的磁势具有如下特点: 源 (1)规定磁势以磁场从转子到定子为正: 这一点主要是为了满足正磁势产生正磁场(磁场由转子到定子为正方向)。 爱 (2)任意两点的磁势差等于该两点之间所有电枢导体电流的代数和; 国 这一点是为了满足磁路高斯定理,即安培环路定律。 荣 (3)磁势波形正、负半波面积相等: 这一点是必须遵循电流连续性原理,并满足空间磁通连续。 校 厚 (4)磁势波形是周期性的; 德 这一点是因为交流绕组电流空间是周期分布的。 对于整数槽绕组,周期是一对磁极距离。 载 物 需要注意的是,尽管实际电机绕组是安放在铁芯槽内的,但是在计算磁势时 假设电流是集中在电枢表面槽口处,这样磁势波只在槽口位置发生突变,突 自 变量为所关注的槽内导体总电流。在分析磁势波形时,不关心绕组端部连接 强 方式,只关心槽内导体电流方向和导体数。这是因为磁势波形主要与气隙磁 场相关联,不考虑漏磁场问题。 不 息 2022-3-12 上海交通大学电气工程系谢宝昌 3
饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 3 磁势的概念 磁势是电枢表面电流空间分布的累积描述,既是电流时间变化的函数,又是 空间位置的函数。交流电枢绕组的磁势具有如下特点: (1)规定磁势以磁场从转子到定子为正; 这一点主要是为了满足正磁势产生正磁场(磁场由转子到定子为正方向)。 (2)任意两点的磁势差等于该两点之间所有电枢导体电流的代数和; 这一点是为了满足磁路高斯定理,即安培环路定律。 (3)磁势波形正、负半波面积相等; 这一点是必须遵循电流连续性原理,并满足空间磁通连续。 (4)磁势波形是周期性的; 这一点是因为交流绕组电流空间是周期分布的。 对于整数槽绕组,周期是一对磁极距离。 需要注意的是,尽管实际电机绕组是安放在铁芯槽内的,但是在计算磁势时 假设电流是集中在电枢表面槽口处,这样磁势波只在槽口位置发生突变,突 变量为所关注的槽内导体总电流。在分析磁势波形时,不关心绕组端部连接 方式,只关心槽内导体电流方向和导体数。这是因为磁势波形主要与气隙磁 场相关联,不考虑漏磁场问题
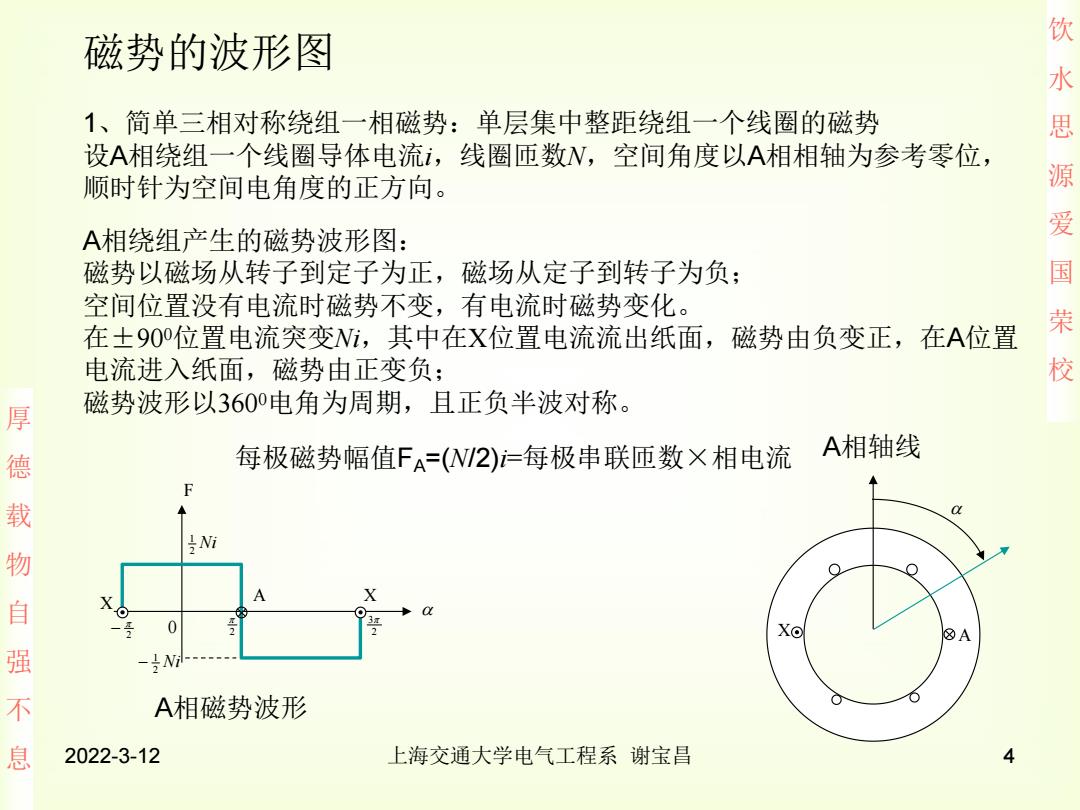
磁势的波形图 饮 水 1、简单三相对称绕组一相磁势:单层集中整距绕组一个线圈的磁势 思 设A相绕组一个线圈导体电流i,线圈匝数N,空间角度以A相相轴为参考零位, 顺时针为空间电角度的正方向。 源 A相绕组产生的磁势波形图: 爱 磁势以磁场从转子到定子为正,磁场从定子到转子为负; 国 空间位置没有电流时磁势不变,有电流时磁势变化。 在±90位置电流突变Wi,其中在X位置电流流出纸面,磁势由负变正,在A位置 荣 电流进入纸面,磁势由正变负: 校 磁势波形以360电角为周期,且正负半波对称。 厚 德 每极磁势幅值FA=(NW2)=每极串联匝数×相电流 A相轴线 F 载 Ni 物 自 0 X⊙ A 强 不 A相磁势波形 息 2022-3-12 上海交通大学电气工程系谢宝昌 4
饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 4 磁势的波形图 1、简单三相对称绕组一相磁势:单层集中整距绕组一个线圈的磁势 设A相绕组一个线圈导体电流i,线圈匝数N,空间角度以A相相轴为参考零位, 顺时针为空间电角度的正方向。 A相绕组产生的磁势波形图: 磁势以磁场从转子到定子为正,磁场从定子到转子为负; 空间位置没有电流时磁势不变,有电流时磁势变化。 在±90 0位置电流突变Ni,其中在X位置电流流出纸面,磁势由负变正,在A位置 电流进入纸面,磁势由正变负; 磁势波形以360 0电角为周期,且正负半波对称。 X A A相轴线 每极磁势幅值FA=(N/2)i=每极串联匝数×相电流 A相磁势波形 F 0 2 2 2 3 Ni 2 1 Ni 2 1 A X X

饮 磁势的波形图 水 2、双层整数槽集中短距绕组一相每对极两个线圈的磁势 思 设A相绕组每对极两个线圈导体电流i,线圈匝数N。,空间角度以A相相轴为参考 源 零位,顺时针为空间电角度的正方向。短距线圈节距系数B=yπ 爱 A相绕组产生的磁势波形图:短距线圈AX和A2X2,有电流时磁势变化。在线圈 国 导体所在位置磁势波形突变N,i,磁势波形以360电角为周期,且磁势正负半波 对称。磁势波形也可看成是线圈导体AX和A2X组成的整距线圈磁势的合成。 荣 校 厚 每极磁势幅值FA=N=每极串联匝数×相电流 A相轴线 德 载 iNi 物 X2 X A ⊙⊙ -B受 0 B -B受 0 自 -Ni 8 A 强 A相两个线圈合成磁势波形 A相两个等价整距线圈磁势波形 不 息 2022-3-12 上海交通大学电气工程系谢宝昌 5
饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 5 磁势的波形图 2、双层整数槽集中短距绕组一相每对极两个线圈的磁势 设A相绕组每对极两个线圈导体电流i,线圈匝数Nc,空间角度以A相相轴为参考 零位,顺时针为空间电角度的正方向。短距线圈节距系数 A相绕组产生的磁势波形图:短距线圈A1X1和A2X2,有电流时磁势变化。在线圈 导体所在位置磁势波形突变Nc i,磁势波形以3600电角为周期,且磁势正负半波 对称。磁势波形也可看成是线圈导体A1X2和A2X1组成的整距线圈磁势的合成。 每极磁势幅值FA=Nc i=每极串联匝数×相电流 A相两个线圈合成磁势波形 A1 X1 A相轴线 A2 X2 F 0 2 2 N i c N i c X1 A1 A2 X2 X1 y / F 0 2 2 N i 2 c 1 N i 2 c 1 X A2 X1 1 A1 X2 A相两个等价整距线圈磁势波形
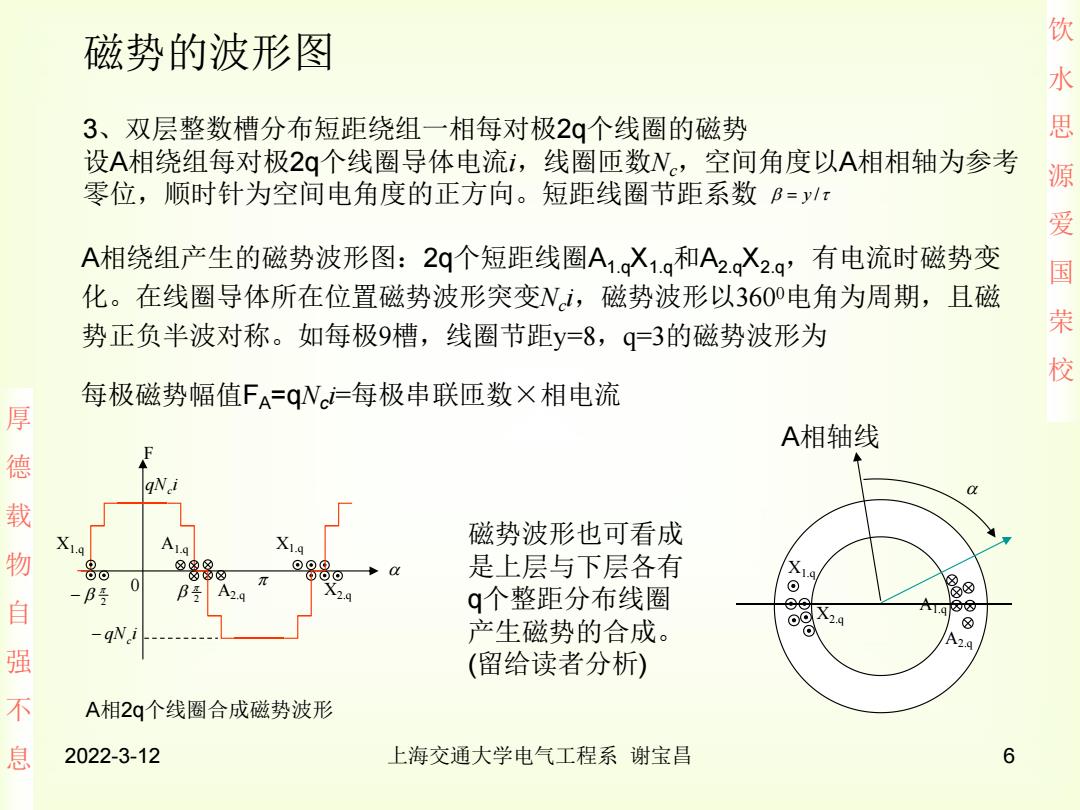
饮 磁势的波形图 水 3、双层整数槽分布短距绕组一相每对极2q个线圈的磁势 思 设A相绕组每对极2q个线圈导体电流i,线圈匝数N,空间角度以A相相轴为参考 零位,顺时针为空间电角度的正方向。短距线圈节距系数B=yπ 源 爱 A相绕组产生的磁势波形图:2q个短距线圈A1.gX1.g和A2.gX2a,有电流时磁势变 国 化。在线圈导体所在位置磁势波形突变Ni,磁势波形以360电角为周期,且磁 势正负半波对称。如每极9槽,线圈节距y=8,q=3的磁势波形为 荣 校 每极磁势幅值FA=qN=每极串联匝数×相电流 厚 A相轴线 德 qNi 载 物 14 磁势波形也可看成 OO④ ǒ可 是上层与下层各有 -B号 0 B号 A2.q 2 2.q q个整距分布线圈 烟 自 ⑧ -gN i 产生磁势的合成。 A2.9 强 (留给读者分析) 不 A相2q个线圈合成磁势波形 息 2022-3-12 上海交通大学电气工程系谢宝昌 6
饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 6 磁势的波形图 3、双层整数槽分布短距绕组一相每对极2q个线圈的磁势 设A相绕组每对极2q个线圈导体电流i,线圈匝数Nc,空间角度以A相相轴为参考 零位,顺时针为空间电角度的正方向。短距线圈节距系数 A相绕组产生的磁势波形图:2q个短距线圈A1.qX1.q和A2.qX2.q,有电流时磁势变 化。在线圈导体所在位置磁势波形突变Nc i,磁势波形以360 0电角为周期,且磁 势正负半波对称。如每极9槽,线圈节距y=8,q=3的磁势波形为 每极磁势幅值FA=qNc i=每极串联匝数×相电流 A相2q个线圈合成磁势波形 y / A1.q X1.q A相轴线 A2.q X2.q F 0 2 2 qN i c qN i c A2.q X1.q A1.q X1.q X2.q 磁势波形也可看成 是上层与下层各有 q个整距分布线圈 产生磁势的合成。 (留给读者分析)

饮 磁势的波形图 水 思 对于整数槽绕组来说,每相每极磁势的波形是以360电角为周期且正负半波对称 的阶梯波,阶梯波的台阶取决于所关注的槽内导体总电流。 源 每相每极磁势幅值等于每极串联导体数与相电流乘积。电流恒定时,磁势幅值恒 爱 定;电流交变时,磁势幅值交变。幅值位置不变而大小随时间周期变化的磁势称 为脉振磁势。 国 不论电流是否变化,任意时刻磁势是空间对称周期函数,因此可以通过Fourier分 荣 解获得基波和谐波,其中谐波仅仅含有奇次谐波,而没有偶次谐波。 基波是以电机极距为半波长度的空间磁势波,谐波极距为基波极距的谐波次数分 校 厚 之一 德 载 复杂的整数槽绕组的磁势波可以由简单三相绕组的一相磁势波在不同空间位置的 物 合成,这种空间位置的差别是槽间电角的整数倍。因此可以通过先计算简单三相 绕组一相磁势基波和谐波的幅值,然后利用空间复矢量计算合成,将复杂的积分 自 转变成简单的复矢量和运算。 强 不 息 2022-3-12 上海交通大学电气工程系谢宝昌 7
饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 7 磁势的波形图 对于整数槽绕组来说,每相每极磁势的波形是以3600电角为周期且正负半波对称 的阶梯波,阶梯波的台阶取决于所关注的槽内导体总电流。 每相每极磁势幅值等于每极串联导体数与相电流乘积。电流恒定时,磁势幅值恒 定;电流交变时,磁势幅值交变。幅值位置不变而大小随时间周期变化的磁势称 为脉振磁势。 不论电流是否变化,任意时刻磁势是空间对称周期函数,因此可以通过Fourier分 解获得基波和谐波,其中谐波仅仅含有奇次谐波,而没有偶次谐波。 基波是以电机极距为半波长度的空间磁势波,谐波极距为基波极距的谐波次数分 之一 复杂的整数槽绕组的磁势波可以由简单三相绕组的一相磁势波在不同空间位置的 合成,这种空间位置的差别是槽间电角的整数倍。因此可以通过先计算简单三相 绕组一相磁势基波和谐波的幅值,然后利用空间复矢量计算合成,将复杂的积分 转变成简单的复矢量和运算
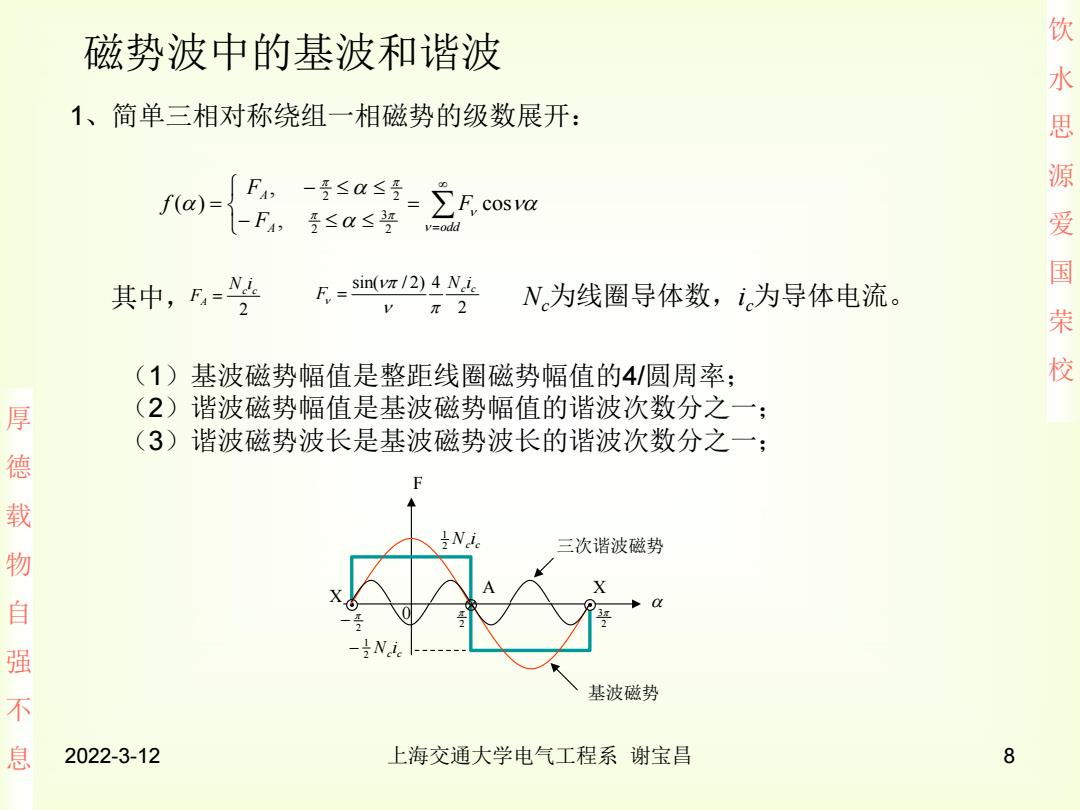
磁势波中的基波和谐波 1、简单三相对称绕组一相磁势的级数展开: 水思 吾≤≤ cosva 其中,学 F=sin(vz/2)4 Ni 源爱国 π2 N为线圈导体数,i为导体电流。 荣 (1)基波磁势幅值是整距线圈磁势幅值的4/圆周率; 校 厚 (2) 谐波磁势幅值是基波磁势幅值的谐波次数分之一; (3)谐波磁势波长是基波磁势波长的谐波次数分之一: 德 F 载 Neie 三次谐波磁势 物 X 自 强 基波磁势 不 息 2022-3-12 上海交通大学电气工程系谢宝昌 8
饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 8 1、简单三相对称绕组一相磁势的级数展开: 磁势波中的基波和谐波 A odd A F F F f cos , , ( ) 2 3 2 2 2 2 sin( / 2) 4 c c N i F 其中, Nc为线圈导体数,ic为导体电流。 (1)基波磁势幅值是整距线圈磁势幅值的4/圆周率; (2)谐波磁势幅值是基波磁势幅值的谐波次数分之一; (3)谐波磁势波长是基波磁势波长的谐波次数分之一; F 0 2 2 2 3 c c N i 2 1 c c N i 2 1 A X X 基波磁势 三次谐波磁势 2 c c A N i F
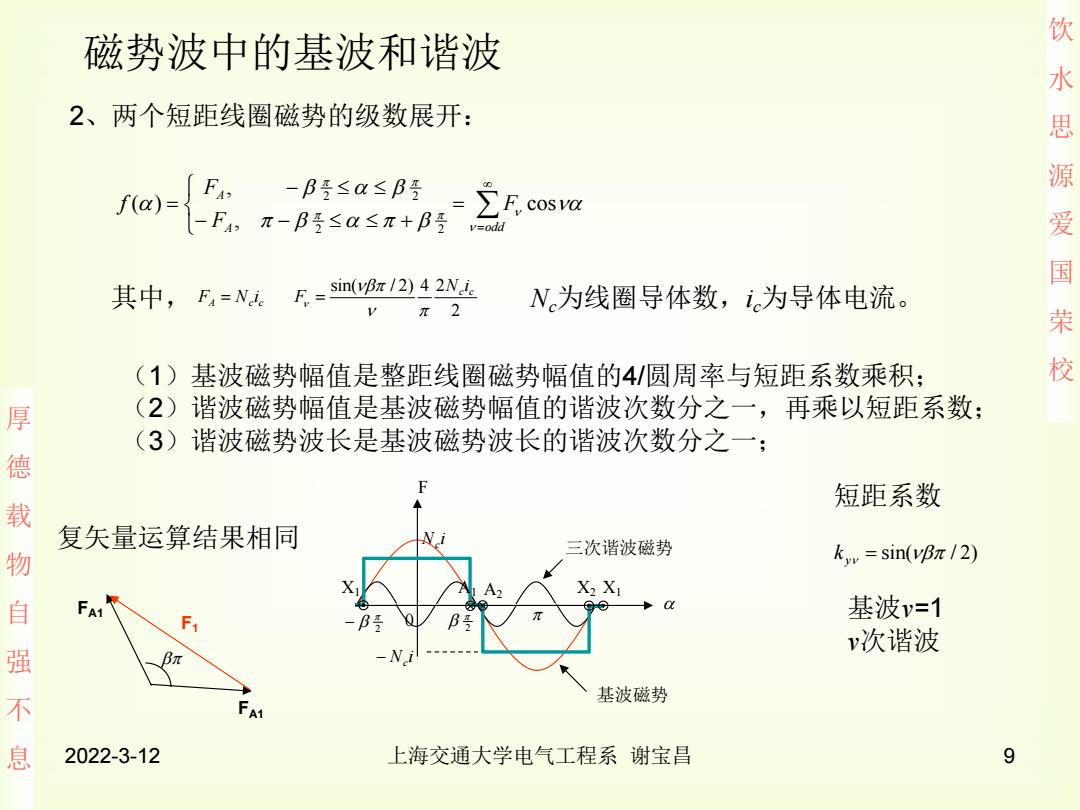
磁势波中的基波和谐波 2、两个短距线圈磁势的级数展开: 水思 f(@- -B受≤a≤B受 -FA,π-B号≤a≤π+B受 y=odd 源爱国 其中,F4=N。 F=sin(vBz/2)4 2Nie π2 N为线圈导体数,i为导体电流。 荣 (1)基波磁势幅值是整距线圈磁势幅值的4/圆周率与短距系数乘积; 校 厚 (2)谐波磁势幅值是基波磁势幅值的谐波次数分之一,再乘以短距系数: (3)谐波磁势波长是基波磁势波长的谐波次数分之一; 德 短距系数 载 复矢量运算结果相同 三次谐波磁势 物 kyv sin(vB/2) X2 X 自 基波v=1 B v次谐波 强 Bπ 基波磁势 不 A1 息 2022-3-12 上海交通大学电气工程系谢宝昌 9
饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 9 2、两个短距线圈磁势的级数展开: 磁势波中的基波和谐波 A odd A F F F f cos , , ( ) 2 2 2 2 2 sin( / 2) 4 2 c c N i F 其中, Nc为线圈导体数,ic为导体电流。 (1)基波磁势幅值是整距线圈磁势幅值的4/圆周率与短距系数乘积; (2)谐波磁势幅值是基波磁势幅值的谐波次数分之一,再乘以短距系数; (3)谐波磁势波长是基波磁势波长的谐波次数分之一; 基波磁势 三次谐波磁势 A c c F N i F 0 2 2 N i c N i c X1 A1 A2 X2 X1 FA1 FA1 F1 sin( / 2) ky 短距系数 基波v=1 v次谐波 复矢量运算结果相同

磁势波中的基波和谐波 3、2q个短距线圈磁势的级数展开: 水思 fa)=∑,cosa 其中,F =sin(vpr/2)sin(va,/2)42qNi 源 sin(va。/2)π2 v=odd 爱 N为线圈导体数,i为导体电流。 国 (1)基波磁势幅值是整距线圈磁势幅值的4/圆周率与绕组系数乘积; 荣 (2)谐波磁势幅值是基波磁势幅值的谐波次数分之一,再乘以绕组系数; (3)谐波磁势波长是基波磁势波长的谐波次数分之一; 校 厚 分布系数 德 载 三次谐波磁势 fir= in(vqa。/2) sin(va。/2) 物 基波v=1 v次谐波 自 %° -B号 B 强 绕组系数kv=kwk 不 基波磁势 息 2022-3-12 上海交通大学电气工程系谢宝昌 10
饮 水 思 源 爱 国 荣 校 厚 德 载 物 自 强 不 息 2022-3-12 上海交通大学电气工程系 谢宝昌 10 3、2q个短距线圈磁势的级数展开: 磁势波中的基波和谐波 odd f F () cos 2 4 2 sin( / 2) sin( / 2) sin( / 2) c c e e q qN i F 其中, Nc为线圈导体数,ic为导体电流。 (1)基波磁势幅值是整距线圈磁势幅值的4/圆周率与绕组系数乘积; (2)谐波磁势幅值是基波磁势幅值的谐波次数分之一,再乘以绕组系数; (3)谐波磁势波长是基波磁势波长的谐波次数分之一; 基波磁势 三次谐波磁势 sin( / 2) sin( / 2) e e q q k 分布系数 基波v=1 v次谐波 e FA1 FA1 F1 FA1 F 0 2 2 qN i c qN i c A2.q X1.q A1.q X1.q X2.q 绕组系数 w y q k k k