上海交通大学：《热力系统设计与实践 Design and Practice of Thermodynamic System》课程教学资源（2017课件）第12-13讲 气体与蒸气的流动 Gas and Steam Flow（开口系节流过程及J-T系数）

2 第7章 气体与蒸气的流动 (Gas and Steam Flow) 上游充通大粤 Mar/17,2017 2 SHANGHAI JLAO TONG UNIVERSIT

Mar/17, 2017 2 2 第 7 章 气体与蒸气的流动 (Gas and Steam Flow)

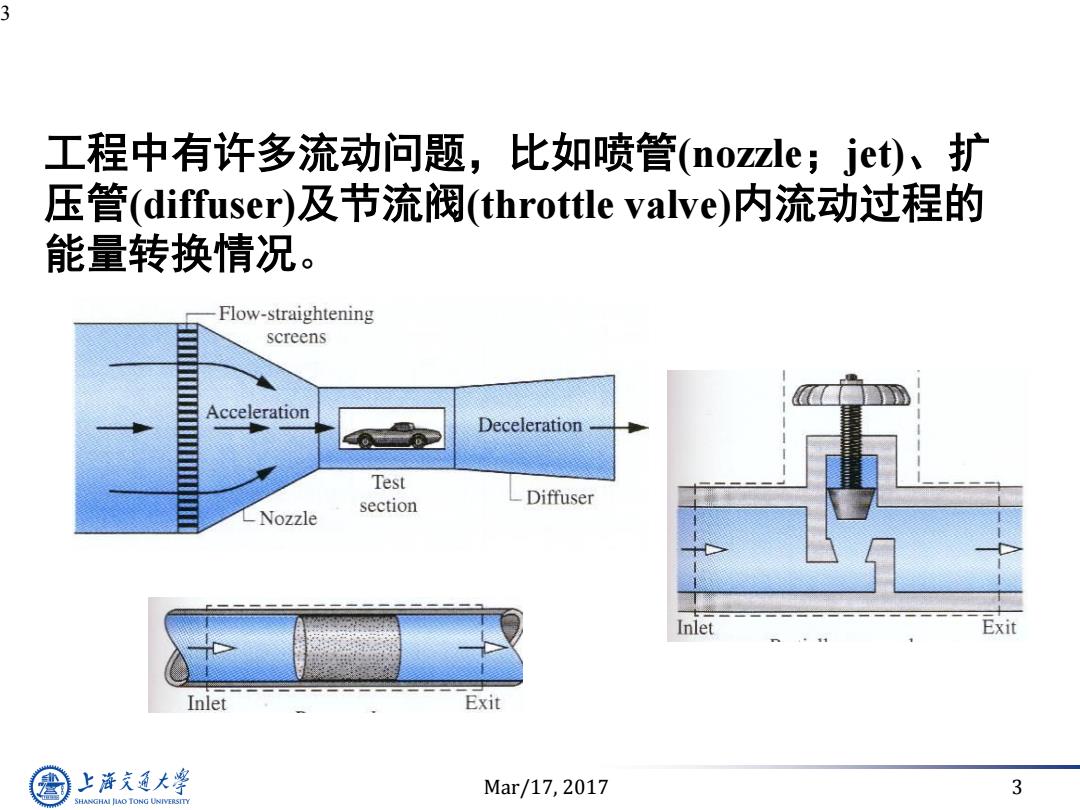
3 工程中有许多流动问题，比如喷管(nozzle;jet)、扩 压管(diffuser)及节流阀(throttle valve)内流动过程的 能量转换情况。 Flow-straightening screens Acceleration Deceleration Test section Diffuser -Nozzle Inlet Exit Inlet Exit 上游充通大学 Mar/17,2017 3 SHANGHAI JIAO TONG UNIVERSITY

Mar/17, 2017 3 3 工程中有许多流动问题，比如喷管(nozzle；jet)、扩 压管(diffuser)及节流阀(throttle valve)内流动过程的 能量转换情况

4 §7-1稳定流动的基本方程式 一.简化 稳定 一 热 可 二稳定流动基本方程 1.质量守恒方程 （连续性方程)-continuity equation A =dm2= P2 V V2 内T编 1m2 dv d cp y A Ce 2 dp dA or dcr =0 A 上游充通大 Mar/17,2017 4 SHANGHAI JLAO TONG UNIVERSITY

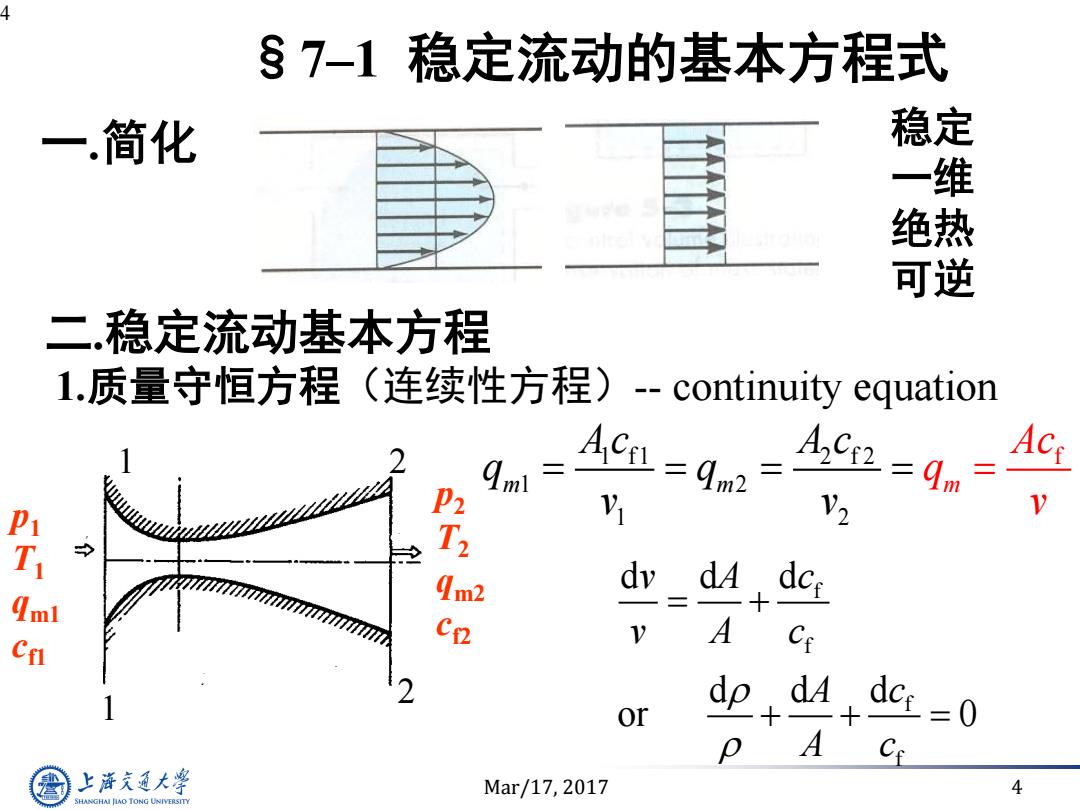
Mar/17, 2017 4 1 1 2 2 p1 T1 qm1 cf1 p2 T2 qm2 cf2 4 二.稳定流动基本方程 1.质量守恒方程（连续性方程）-- continuity equation 1 f1 2 f 2 1 2 1 2 f m m m A c A c Ac q v q q v v      f f f f d d d d d d or 0 v A c v A c A c A c        §7–1 稳定流动的基本方程式 一.简化 稳定 一维 绝热 可逆

5 2.过程方程 Piv=P2v=py* +xd=0 dv p 注意：若水蒸气，则 且T≠T21 3.稳定流动能量方程一steady--flow energy equation 9=△h+5△c+g△+w, 2 若忽略g△上，q≈0，w,=0 A2是+-今+ed=0 2 上游究通大粤 Mar/17,2017 5 SHANGHAI JLAO TONG UNIVERSITY

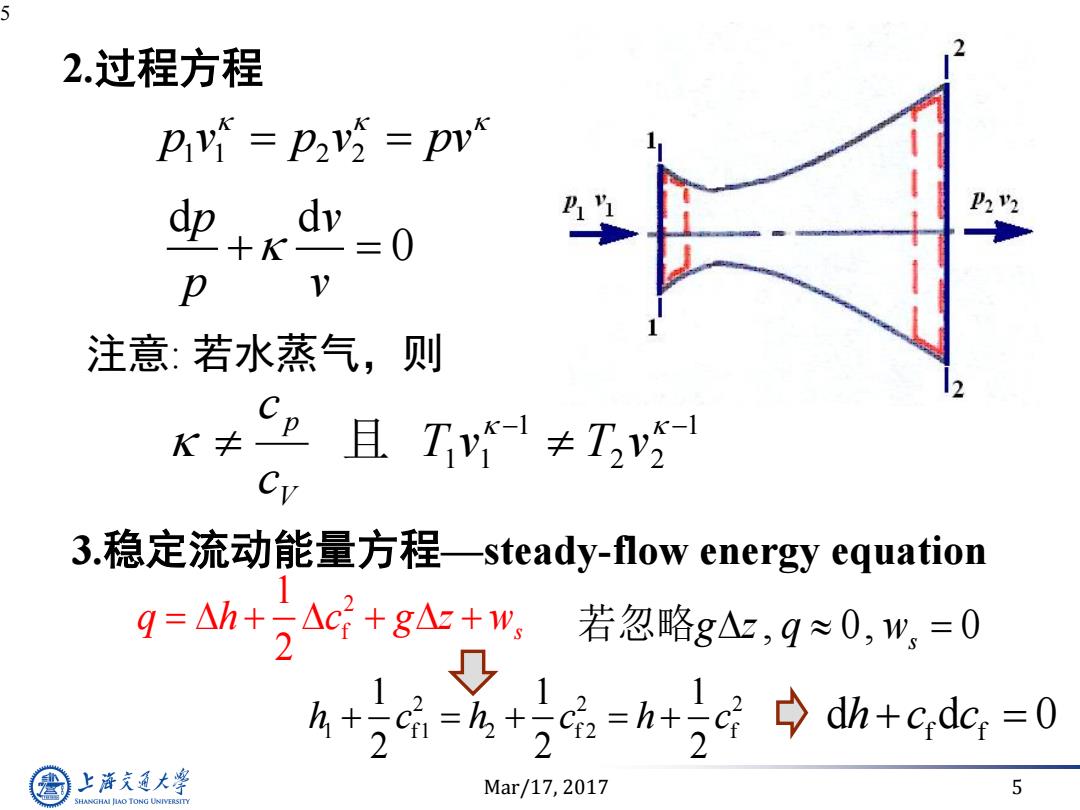
Mar/17, 2017 5 5 2.过程方程    p v  p v  pv 1 1 2 2 注意: 若水蒸气，则 1 2 2 1 1 1        T v T v c c V p 且 3.稳定流动能量方程—steady-flow energy equation 2 f 1 2 s q h c g z w        d d 0 p v p v    , 0, 0 s 若忽略g z q w    2 2 2 1 f1 2 f 2 f 1 1 1 2 2 2 h c h c h c      f f d d 0 h c c  

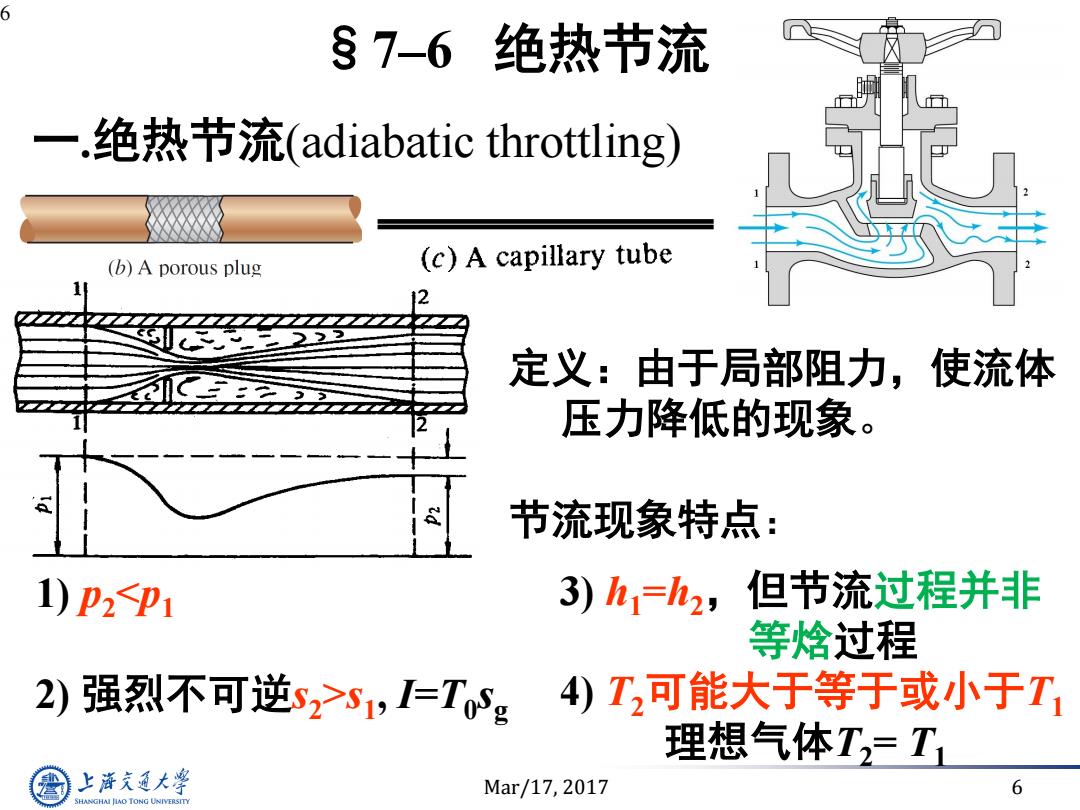
6 §7-6 绝热节流 一.绝热节流(adiabatic throttling) (b)A porous plug (c)A capillary tube 定义：由于局部阻力，使流体 压力降低的现象。 节流现象特点： 1)p21 3)h=h2,但节流过程并非 等焓过程 2) 强烈不可逆s2>S1,I=Tg 4)T,可能大于等于或小于T 理想气体T,=T1 上游充通大 Mar/17,2017 6 SHANGHAI JLAO TONG UNIVERSITY

Mar/17, 2017 6 6 §7–6 绝热节流 一.绝热节流(adiabatic throttling) 定义：由于局部阻力，使流体 压力降低的现象。 1) p2s1 , I=T0 sg 3) h1 =h2，但节流过程并非 等焓过程 4) T2可能大于等于或小于T1 理想气体T2= T1 节流现象特点：

7 二.节流后的温度变化 1.焦耳一汤姆逊系数（Joule-Thomson coefficient) 层- 可 dh 0 ,= h Cp 焦耳一汤姆逊系数 (也称节流微分效应) 节流dp<0 dT取决于T 上游气通大粤 Mar/17,2017 7 HANGHAI JLAO TONG UNIVERSITY

Mar/17, 2017 7 7 二.节流后的温度变化 1.焦耳—汤姆逊系数（Joule-Thomson coefficient ） 据 d d d p p v h c T T v p T                    令 d 0 p J h p v T v T T h p c                      焦耳—汤姆逊系数 （也称节流微分效应） d 0 d p v p T T v T           节流 取决于

8 ，0 4>0,dT0 升温 0 T 4=0,dT=0 不变 如理想气体 dp dy dT 十 p T - -0 →4，≡0，dT=0 →T2=T1 上游充通大学 Mar/17,2017 8 SHANGHAI JLAO TONG UNIVERSITY

Mar/17, 2017 8 8 0 0,d 0 J p v T v T T              降温 如理想气体 d d d 0 p p p v T v v v T v p v T T T T                        0 0,d 0 J p v T v T T              升温 0 0,d 0 J p v T v T T              不变    J 0, d 0 T ⟹ 𝑇2≡ 𝑇1

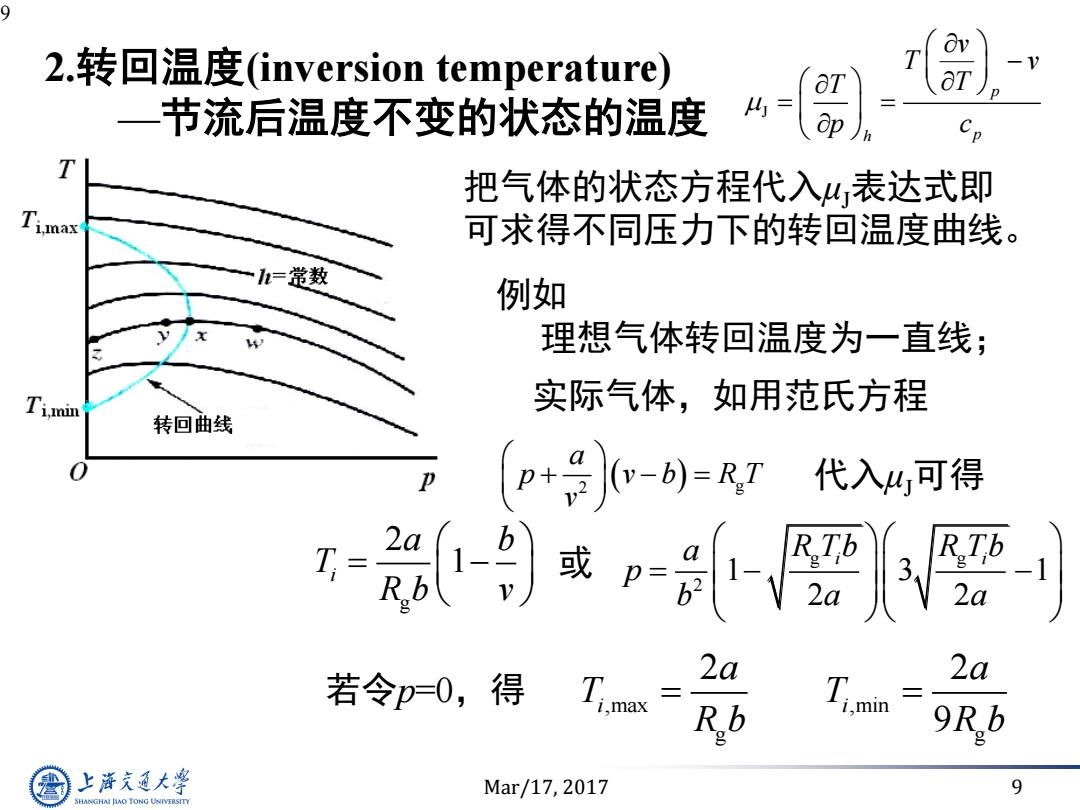
9 2.转回温度(inversion temperature) T 一节流后温度不变的状态的温度 4 ap T 把气体的状态方程代入4表达式即 Timas 可求得不同压力下的转回温度曲线。 一h=常数 例如 理想气体转回温度为一直线； 实际气体，如用范氏方程 转回曲线 (p+是)-创=RT代入可得 -9或密要- 7= 2a 若令p=0,得 Ti.max 2a R.b Ti.in 上游究通大粤 Mar/17,2017 9 SHANGHAI JLAO TONG UNIVERSITY

Mar/17, 2017 9 9 2.转回温度(inversion temperature) —节流后温度不变的状态的温度 把气体的状态方程代入μJ表达式即 可求得不同压力下的转回温度曲线。 例如 理想气体转回温度为一直线； 2   g a p v b R T v          代入μJ可得 g 2 1 i a b T R b v         或 g g 2 1 3 1 2 2 a R T b R T b i i p b a a                实际气体，如用范氏方程 J p h p v T v T T p c                     若令p=0，得 ,max ,min g g 2 2 9 i i a a T T R b R b  

10 3.节流的积分效应 节流时状态在致冷区则T下降 致温区 节流时状态在致温区则，T上升或下 致冷区 降取决于△p的大小 i.min 当气体温度下Timx或TKT:mi, 节流后T上升 P 如： H2 Tmax=-80°C 常温节流后T上升，T2>T1 He T.max =-236C Ti.max =630K N2 Ti.min =100K 常温下节流T下降 Po =40MPa 上游充通大学 Mar/17,2017 10 SHANGHAI JLAO TONG UNIVERSITY

Mar/17, 2017 10 10 • 节流时状态在致冷区则T下降 • 节流时状态在致温区则，T上升或下 降取决于Δp的大小 2 ,max ,max H 80 C He 236 C i i T T     常温节流后T上升，T2>T1 N2 ,max ,min 0 630K 100K 40MPa i i T T p    常温下节流T下降 当气体温度T>Ti,max或T<Ti,min，节流后T上升 如： 3.节流的积分效应

11 三.节流现象的工程应用 气体液化 发动机功率调节 孔板流量计，干度计… 利用4，结合实验，建立实际气体微分方程 热网中蒸汽降压 上游充通大学 Mar/17,2017 11 SHANGHAI JLAO TONG UNIVERSITY

Mar/17, 2017 11 11 三.节流现象的工程应用 气体液化 发动机功率调节 孔板流量计，干度计··· 利用μJ，结合实验，建立实际气体微分方程 热网中蒸汽降压