上海交通大学：《热力系统设计与实践 Design and Practice of Thermodynamic System》课程教学资源（课件讲稿）第14讲 理想气体混合物及湿空气 Ideal gas mixture and moisture（理想气体混合物分压力及状态参数计算）

第12章 理想气体混合物及湿空气 (Ideal gas mixture and moisture) 上游充通大粤 2019年3月29日 2 SHANGHAI JLAO TONG UNIVERSIT

2019年3月29日 2 第 12 章 理想气体混合物及湿空气 (Ideal gas mixture and moisture)

§12-1理想气体混合物 考虑气体混合物的基本原则： 混合气体的组分都处于理想气体状态，测混合气体 也处于理想气体状态； 混合气体可作为某种假想气体，其质量和分子数与 组分气体质量之和及分子数之和相同； n混=∑n, n混M混=∑n,M, pV=m混R混T R混-平均气体常数 M混R混=R M混-平均摩尔质量 (w)o=22.4×10-3m3/mol 等等 理想气体混合物可作为R混和M混的“某种”理想气体。 上商充通大学 2019年3月29日 3 SHANGHAI JLAO TONG UNIVERSITY

2019年3月29日 3 §12–1 理想气体混合物 考虑气体混合物的基本原则：  混合气体的组分都处于理想气体状态，则混合气体 也处于理想气体状态；  混合气体可作为某种假想气体，其质量和分子数与 组分气体质量之和及分子数之和相同； g g pV m R T R   混 混 混 平均气体常数 理想气体混合物可作为Rg混和M混的“某种”理想气体。 M R R M g 混 混   混 平均摩尔质量 3 3 0 ( ) 22.4 10 m / mol Mv    等等 n 混  ni i i n M n M 混 混  

一、混合气体的分压力定律和分容积定律 l.分压力定律(Dalton law of partial pressure) 分压力—组分气体处在与混合气体相同容积、 相同温度时，单独对壁面的作用力。 命母争 pV=nRT PV=nRT PaV=nRT pV =n,RT ∑p,=RT·∑n,=nRT p=∑p 分压力定律 上游充通大 2019年3月29日 4 SHANGHAI JIAO TONG UNIVERSITY

2019年3月29日 4 一、混合气体的分压力定律和分容积定律 1.分压力定律(Dalton law of partial pressure) 分压力——组分气体处在与混合气体相同容积、 相同温度时，单独对壁面的作用力。 pV  nRT 2 2 p1 V  n1 RT p V n RT  Vpi  RT ni  nRT i p p   pi V  ni RT 分压力定律

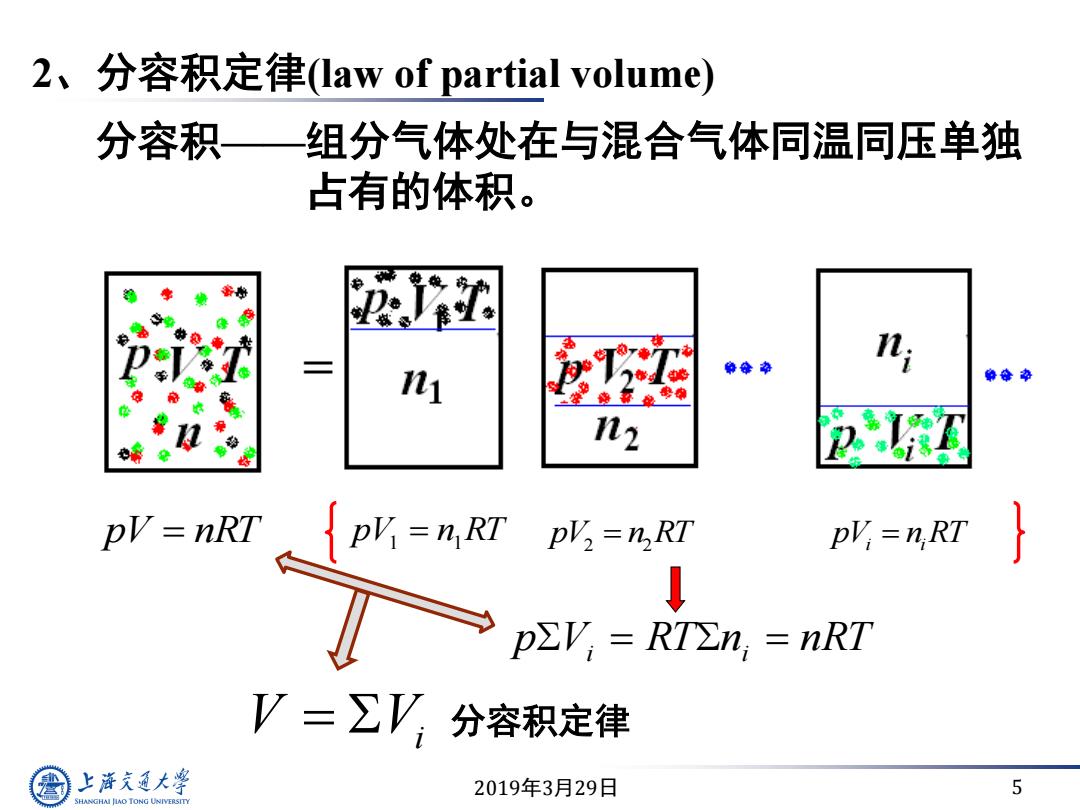
2、分容积定律(law of partial volume) 分容积— 组分气体处在与混合气体同温同压单独 占有的体积。 命 命年争 12 2 p'=nRT。{pH=nRTp=%Rr pV;=n,RT p∑V,=RT∑n,=nRT V=∑V, 分容积定律 上游充通大学 2019年3月29日 5 SHANGHAI JLAO TONG UNIVERSITY

2019年3月29日 5 2、分容积定律(law of partial volume) 分容积——组分气体处在与混合气体同温同压单独 占有的体积。 pV  nRT pV1  n1 RT 2 2 pV n RT  i i pV n RT  pVi  RTni  nRT V V   i 分容积定律

三、混合气体成分 l.质量分数(mass fraction of a mixture) ,-限 2w,=1 m 2.体积分数(volume fraction of a mixture) ∑0，=1 V 3.摩尔分数(mole fraction of a mixture) ∑x,=1 n 图 上游充通大学 2019年3月29日 6 SHANGHAI JLAO TONG UNIVERSIT

2019年3月29日 6 三、混合气体成分   i 1 i i w m m w 2.体积分数(volume fraction of a mixture)   i 1 i i V V   3.摩尔分数(mole fraction of a mixture)   i 1 i i x n n x 1.质量分数(mass fraction of a mixture)

4.各成分之间的关系 a）x,=9·0,= n(Mv),n=x 混n(w)混 n混 b)1 ，= R Re M混 pV;/(RT) .W= V Ro =0.Ro R腿一XRg R m pV(RT)V混R R/M =X RIMi M M混 c) pi=xp X= h=p,'(RT)=2 n混 pV/(RT)P 上游气通大粤 2019年3月29日 7 HANGHAI JIAO TONG UNIVERSITY

2019年3月29日 7 4.各成分之间的关系 ) i i a x   g g ) i i i i i R M w x x R M b   混 混 i i V V   混     i i i i n Mv n x n Mv n    混 混 混 g g g g g g g g /( ) /( ) / / i i i i i i i i i i i i i i m V pV R T R R R w x m pV R T V R R R R M M x x R M M         混 混 混 混 混 混 混 ) i i c p x p  /( ) /( ) i i i i n pV RT p x n pV RT p    混

5.利用混合物成分求M混和Rg混 a)已知质量分数 R混=(w,R)→M混=7 R →wR=(Rg混x)=R混x,=R混 b)已知摩尔分数 R M混=(M,x)→R混= M混 :M=(%4,)M2=3 n混 上游究通大粤 2019年3月29日 8 HANGHAI JLAO TONG UNIVERSITY

2019年3月29日 8 5.利用混合物成分求M混和Rg混 a)已知质量分数 R w R g g 混   i i g R M R   混 混   g g g g g g i i i i i i i R w x w R R x R x R R         混 混 混 混 b)已知摩尔分数  i i g R M M x R M 混 混     混       i i i i i i i i n M n n M n M M M x M n n                混 混 混 混 混

例题1第三章\A711143 已知二元理想混合气体在温度T(K),压力p(Pa)时的 密度p(kgm3),试确定该混合气体的质量分数w 解： V混= = p 0 :Rg混=∑w,R=WR1+w,R2=(1-w2)R1+w,R2 (.w=1) Rg混-R1 同理 R2混-R2 Rg2-Ra Rat-Rg2 上游气通大粤 2019年3月29日 9 SHANGHAI JLAO TONG UNIVERSITY

2019年3月29日 9 已知二元理想混合气体在温度T (K)，压力p (Pa)时的 密度ρ (kg/m3 )，试确定该混合气体的质量分数wi。 解： T p R p R T v g g        混 混 混 1 g 1 g1 2 g2 2 g1 2 g2   g 1 R w R w R w R w R w R 混        i i (  1)  wi g g1 2 g2 g1 R R w R R     混 例题\第三章\A711143 g g 2 1 g1 g2 R R w R R    同理 混

例题1第三章\A411143 由A、B两种气体组成的混合气体，若质量分数wA>wB,是 否一定有摩尔分数xA>xB,为什么？试以H2和CO2混合物， H,=0.1,wco,=0.9说明之。 解： R R Wi M .Rg 即取决于 M M,Rg混 R混=∑RgW,=RH,WH,+Rco,Wc0, =4.124kJ/kgK)×0.1+0.189kJ/kg·K)×0.9=0.5825kJ/kg·K) R业wH,=05825 :X二Re混 4.124 ×0.1=0.708 0.189 XcO2 Rg混 ×0.9=0.292 0.5825 上游气通大粤 2019年3月29日 10 SHANGHAI JLAO TONG UNIVERSITY

2019年3月29日 10 由A、B两种气体组成的混合气体，若质量分数wA>wB ,是 否一定有摩尔分数xA>xB ,为什么？试以H2和CO2混合物， H CO 2 2 w w   0.1 0.9 ， 说明之。 解： g g i i i R x w R  混 g g i i i i i R R w R x M R M     混 g i i w M R 混 即取决于 2 2 2 2 g g gH H gCO CO 4.124kJ/(kg K) 0.1 0.189kJ/(kg K) 0.9 0.5825kJ/(kg K) R R w R w R w     i i         混 例题\第三章\A411143 2 2 2 2 2 2 gH H H g gCO CO CO g 4.124 0.1 0.708 0.5825 0.189 0.9 0.292 0.5825 R x w R R x w R          混 混 CO H 2 2 x x 

四、理想气体混合物的比热容、热力学能、焓和熵 a.比热容 C混=∑w,C, C混=x,C, Cm混=∑x,Cm Cmp-Cmr =R U b.热力学能 U混=∑U, 混= ∑mui=2(w,u1) m m c.焓H混=H,=(U,+p,=U,+VP,=U+pV 二 H >mh.=(wh) n m m d.熵S混=∑S,=∑m,S, S混=W,S s,=f(T,p) 上游充通大学 2019年3月29日 11 HANGHAI JLAO TONG UNIVERSITY

2019年3月29日 11 四、理想气体混合物的比热容、热力学能、焓和熵 a.比热容 ' ' m m m m i i i i i i p v c w c C x C C x C C C R         混 混 混 b.热力学能 ( ) i i i i i w u m m u m U U U u    混   混   c.焓   ( ) i i i i i i i i i i H H U pV U V p U pV H H m h h w h m m m                   混 混 混 d.熵 i i i i i S S m s s w s       混 混 ( , ) i i s f T p 