
第二章测试系统的动态特征 第一节测量系统在瞬变参数测量中的动态特性 第二节测量系统的动态响应 第三节测量系统的动态标定
1 第二章 测试系统的动态特征 第一节 测量系统在瞬变参数测量中的动态特性 第二节 测量系统的动态响应 第三节 测量系统的动态标定
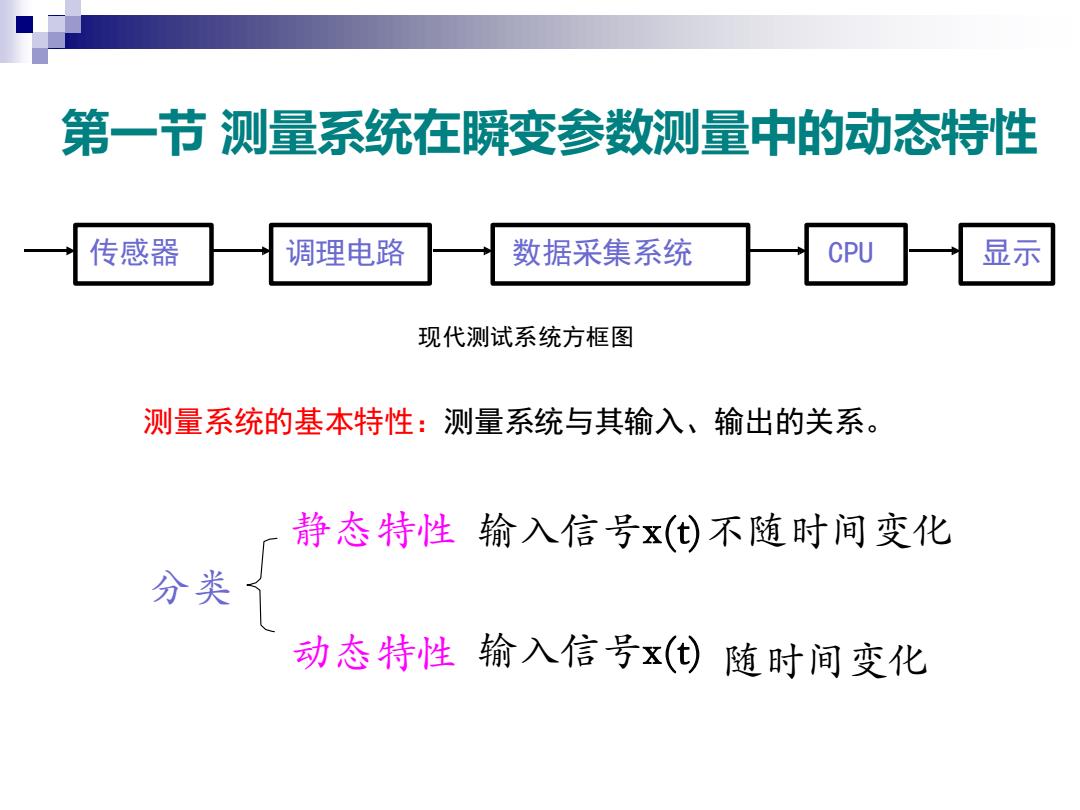
第一节测量系统在瞬变参数测量中的动态特性 传感器 调理电路 数据采集系统 CPU 显示 现代测试系统方框图 测量系统的基本特性:测量系统与其输入、输出的关系。 静态特性输入信号x()不随时间变化 分类了 动态特性输入信号x(①)随时间变化
第一节 测量系统在瞬变参数测量中的动态特性 现代测试系统方框图 测量系统的基本特性:测量系统与其输入、输出的关系。 静态特性 输入信号x(t)不随时间变化 动态特性 分类 输入信号x(t) 随时间变化 传感器 调理电路 数据采集系统 CPU 显示

一、动态特性的数学描述 时域中的微分方程 幅频域中的传递函数 频率域中频域特性 3
3 一、动态特性的数学描述 幅频域中的传递函数 频率域中频域特性 时域中的微分方程

(1)微分方程 d"y+ d"y d yaoy +…+4dt x(t) an dt" =b. x+bd d"x dx dt" +…+b行+bo\ y() 特点 概念清晰,输入-输出关系明了,可区分 暂态响应和稳态响应,但求解方程困难
(1)微分方程 特点 y(t) x(t) 概念清晰,输入-输出关系明了,可区分 暂态响应和稳态响应,但求解方程困难
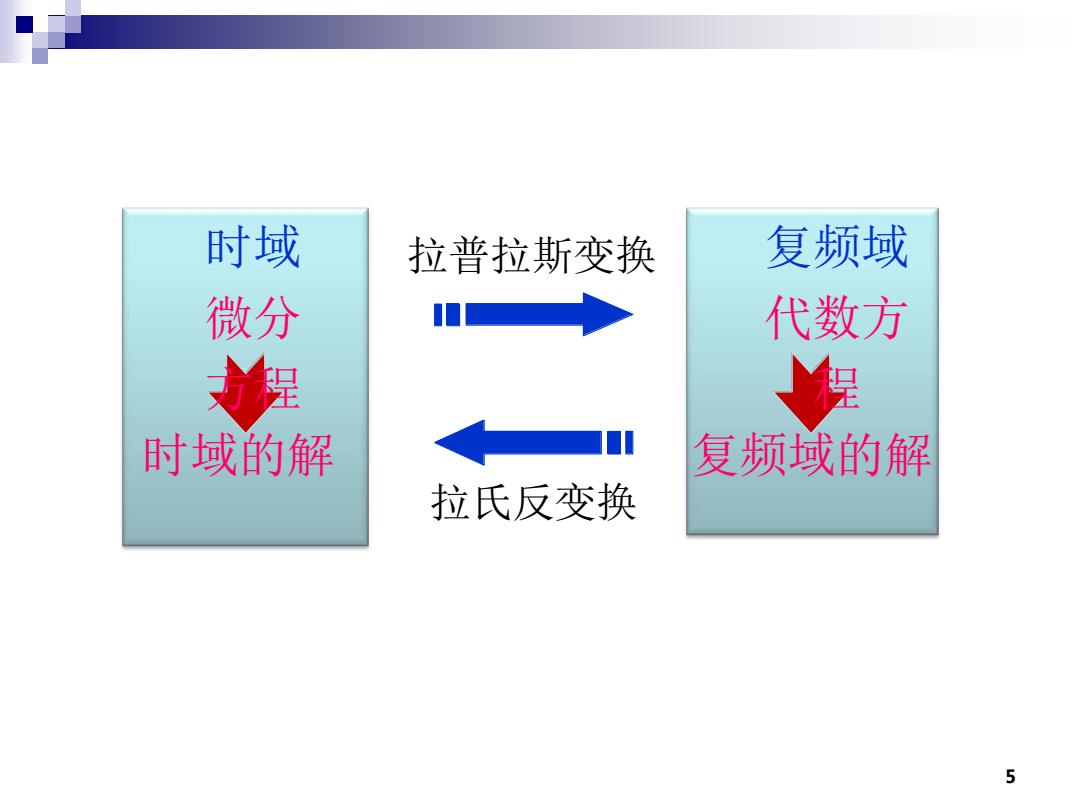
时域 拉普拉斯变换 复频域 微分 代数方 时域的解 复频域的解 拉氏反变换 5
5 时域 微分 方程 复频域 代数方 程 拉普拉斯变换 时域的解 复频域的解 拉氏反变换

拉普拉斯变换的定义 若时间函数f) 在t>0有定义,则f) 的 拉普拉斯变换(简称拉氏变换)为 L(f()》=F(s)=∫7i)e"d S—1 复变量(复频率),S=0+j0 f(t)一F(s)的原函数 F(s=LIf F(s)一f(t)的象函数 8
6 若时间函数 f(t) 在 t > 0 有定义,则 f(t) 的 拉普拉斯变换(简称拉氏变换)为 -st d ∫ L( f (t)) = F(s) = f (t)e s — 复变量(复频率),s = σ + jω f(t)— F(s)的原函数 F(s) — f(t)的象函数 F(s)=L[f(t)] ∞ 0 拉普拉斯变换的定义

(2)传递函数(Transfer function) 定义传递函数是输出信号与输入信号之比。 b sm+b sm1+...+b.s+b H(s)= Y(s) X(sas”+a,s"-1+…+as+a 分母中的s的幂次n代表系统微分方程的阶数。 优点表示了传感器本身特性,与输入输出无关, 可通过实验求得。 7
7 (2)传递函数(Transfer function) 定义传递函数是输出信号与输入信号之比。 m m −1 1 0 H(s) = = n n−1 1 0 分母中的s的幂次n代表系统微分方程的阶数。 优点 表示了传感器本身特性,与输入输出无关, 可通过实验求得。 Y (s) b s m + b s m−1 ++ b s + b X (s) a s n + a s n −1 ++ a s + a

传递函数的特性 >仅描述系统本身的动态特性,与输入和初始 条件无关。 >不说明被描述系统的物理结构,不论是电路 结构还是机械结构,只要动态特性相似均可用 同一类传递函数来描述。 >传递函数的分母取决于系统的结构(输入方 式、被测量及测点布置等) 热能与动力机械测试技术 8
8 传递函数的特性 ➢ 仅描述系统本身的动态特性,与输入和初始 条件无关。 ➢ 不说明被描述系统的物理结构,不论是电路 结构还是机械结构,只要动态特性相似均可 用 同一类传递函数来描述。 ➢ 传递函数的分母取决于系统的结构(输入方 式、被测量及测点布置等) 热能与动力机械测试技术

测试装置的传递函数的求取步骤 1.分析系统,根据物理学的相关定律写出描述 系统的微分方程。 2.假设全部初始条件等于零,取微分方程的拉 式变化(利用拉式变换的微分性质) 3.写出传递函数的表达式:H=Y (s) 9
9 测试装置的传递函数的求取步骤 分析系统,根据物理学的相关定律写出描述 系统的微分方程。 1. 假设全部初始条件等于零,取微分方程的拉 式变化(利用拉式变换的微分性质) 2. 写出传递函数的表达式: Y(s) 3. H(s) = X (s)
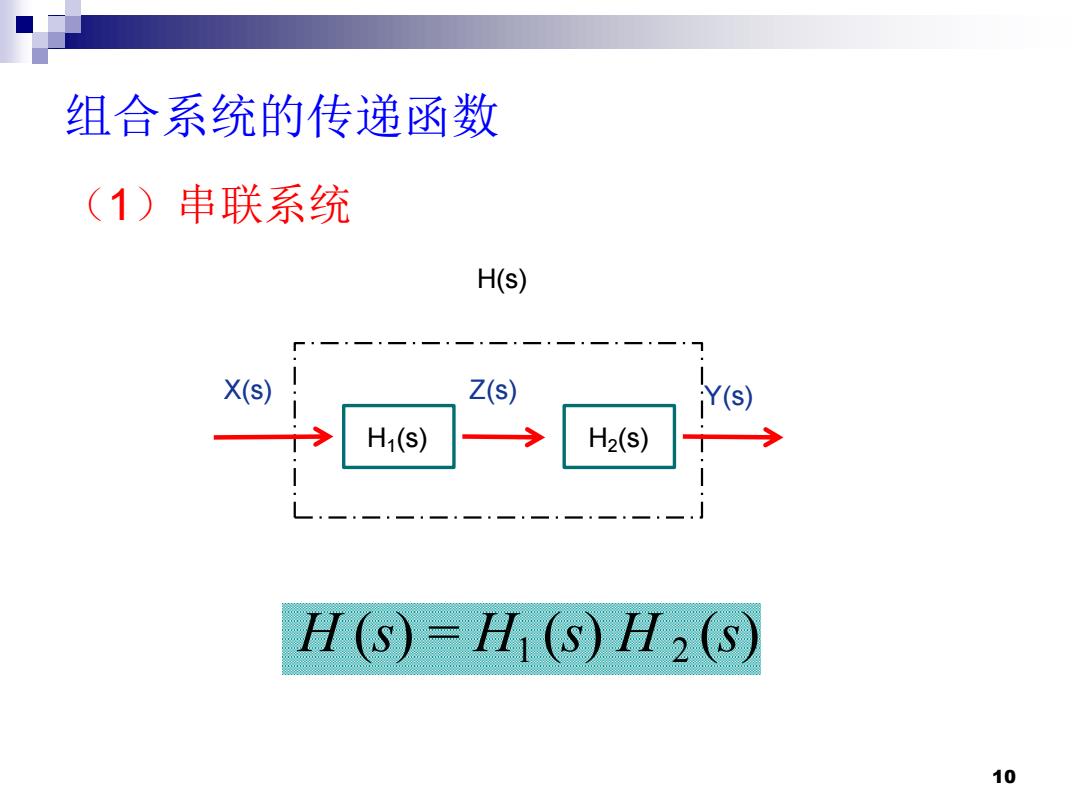
组合系统的传递函数 (1)串联系统 H(s) X(s) Z(s) Y(s) H1(S) H2(S) H(S)=Hi(s)H2(s) 10
10 组合系统的传递函数 H1 (s) H2 (s) X(s) Z(s) Y(s) H(s) H (s) = H1 (s) H 2 (s) (1)串联系统