
第六章 种用价值的评定 基因型选择 甘肃农业大学动物科学技术学院 2023/5/23
2023/5/23 1 第六章 种用价值的评定 ——基因型选择 甘肃农业大学动物科学技术学院

>基因型选择是以表型选择为基础,根据被选对象本身或其祖先、 同胞及后裔的遗传性能表现进行选择。 >基因型选择,若为质量性状,则可根据简单的孟德尔定律进行遗 传分析,判断基因型,选择比较容易;若为数量性状,由于正确判 断其基因型比较困难,所以必须根据被选个体本身及其祖先、同胞 和后裔的表型值来预测育种值,然后根据育种值的大小进行选择。 2023/5/23 2
2023/5/23 2 ➢基因型选择是以表型选择为基础,根据被选对象本身或其祖先、 同胞及后裔的遗传性能表现进行选择。 ➢基因型选择,若为质量性状,则可根据简单的孟德尔定律进行遗 传分析,判断基因型,选择比较容易;若为数量性状,由于正确判 断其基因型比较困难,所以必须根据被选个体本身及其祖先、同胞 和后裔的表型值来预测育种值,然后根据育种值的大小进行选择

一、育种值的概念和特征 1、基因型值和群体均值的关系 对于式PG叶E: 在作为整体看待的群体中,环境影响有好有坏,但平均环境离差为零, 因而一个群体的平均表型值等于其平均基因型值。 为便于分析,以一个位点对表型值的影响来说明不同基因型值和群体 平均表型值的关系。 假设位点A上有一对等位基因A1与A2,A1A1的基因型值为+a,A2A2的基 因型值为-a(无论A1A1与A2A2的实际值是多少,在两个值的均数为0的情 况下,都可以用相等的绝对值来代表两者),A1A2的基因型值为d 基因型 A2A2 A1A2 A1A1 基因型值-a d +a 任意指定的基因型值 图中坐标原点,即零值点,位于两纯合体数值的中点上。A1A2的基因型值取 决于显性度(degree of dominance),即a/d,若没有显性,d0;若A1对A2 为显性,d值为正;若A2对A1为显性,d值为负;当显性完全时,a±a。 2023/5/23
2023/5/23 3 对于式P=G+E : 在作为整体看待的群体中,环境影响有好有坏,但平均环境离差为零, 因而一个群体的平均表型值等于其平均基因型值。 为便于分析,以一个位点对表型值的影响来说明不同基因型值和群体 平均表型值的关系。 假设位点A上有一对等位基因A1与A2,A1A1的基因型值为+a,A2A2的基 因型值为-a(无论A1A1与A2A2的实际值是多少,在两个值的均数为0的情 况下,都可以用相等的绝对值来代表两者),A1A2的基因型值为d 基因型 A2A2 A1A2 A1A1 –––|–––––––––––––––––|–––––––|––––––––––|––– 基因型值 -a 0 d +a 任意指定的基因型值 图中坐标原点,即零值点,位于两纯合体数值的中点上。A1A2的基因型值取 决于显性度(degree of dominance),即a/d,若没有显性,d=0;若A1对A2 为显性,d值为正;若A2对A1为显性,d值为负;当显性完全时,d=±a。 一、育种值的概念和特征 1、基因型值和群体均值的关系
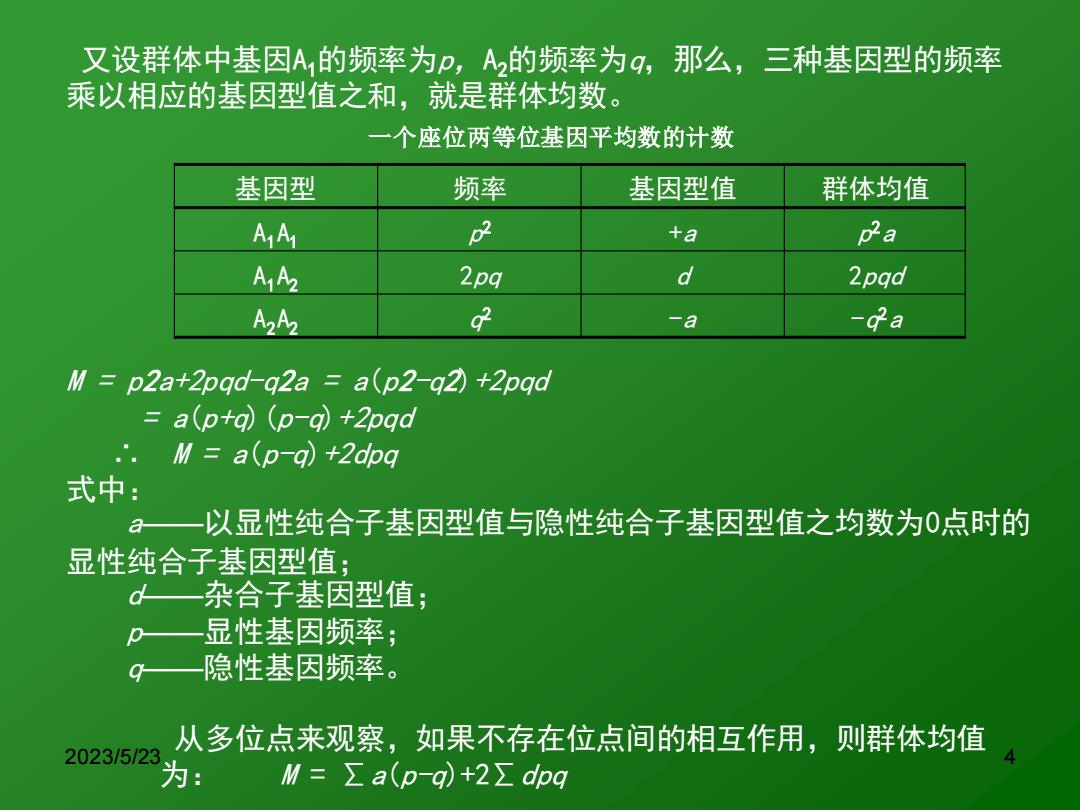
又设群体中基因A的频率为p,A的频率为q,那么,三种基因型的频率 乘以相应的基因型值之和,就是群体均数。 一个座位两等位基因平均数的计数 基因型 频率 基因型值 群体均值 AA 2 +a pa AA2 2pq d 2pqd A2A2 g -a -da M p2a+2pqd-g2a a(p2-g2)+2pqd a(p+q)(p-q)+2pqd ∴.M=a(p-q)+2dpg 式中: a一以显性纯合子基因型值与隐性纯合子基因型值之均数为0点时的 显性纯合子基因型值; d—杂合子基因型值; Q 显性基因频率; 隐性基因频率。 从多位点来观察,如果不存在位点间的相互作用,则群体均值 2023/5/23 为: M=Σa(p-q)+2∑dpg
2023/5/23 4 又设群体中基因A1的频率为p,A2的频率为q,那么,三种基因型的频率 乘以相应的基因型值之和,就是群体均数。 一个座位两等位基因平均数的计数 基因型 频率 基因型值 群体均值 A1A1 p 2 +a p 2a A1 A2 2pq d 2pqd A2A2 q 2 -a -q 2a 从多位点来观察,如果不存在位点间的相互作用,则群体均值 为: M = ∑a(p-q)+2∑dpq M = p2a+2pqd-q2a = a(p2-q2)+2pqd = a(p+q)(p-q)+2pqd ∴ M = a(p-q)+2dpq 式中: a——以显性纯合子基因型值与隐性纯合子基因型值之均数为0点时的 显性纯合子基因型值; d——杂合子基因型值; p——显性基因频率; q——隐性基因频率

2、基因的平均效应 特定基因以随机方式与群体的基因样本相结合而形成合子的平均基 因型值对群体均值的离差,就是该基因在特定群体中的平均效应。 例如,基因A,在某个群体中的平均效应。假设这个群体在A位点有A1、A2 两个等位基因,其频率各为和9。基因A,以随机方式与这个群体的基因 相结合,势必产生AA与A,A,两种基因型;两种基因型的频率应当与群 体中两种基因的频率相等,也就是会产生比例为的AA1,比例为g的 A1A20 这些合子的均值为:patqd 与群体均值的离差则是:a1=pa+gd-[a(p-q)+2dpg] g[atd(g-p)] 如a=a+d(q-p),a1=qa p、q 分别代表群体中显性基因与隐性基 这就是基因A的平均效应。 因的频率; 可得A,的平均效应为: ad二分别代表显性纯合子与杂合子的基 因型值: a2 =pLatd(q-p)]=-pa a1- 显性基因(在群体中的)平均效应; 2023/5/23 a2— 隐性基因的平均效应
2023/5/23 5 2、基因的平均效应 特定基因以随机方式与群体的基因样本相结合而形成合子的平均基 因型值对群体均值的离差,就是该基因在特定群体中的平均效应。 例如,基因A1在某个群体中的平均效应。假设这个群体在A位点有A1、A2 两个等位基因,其频率各为p和q。基因A1以随机方式与这个群体的基因 相结合,势必产生A1A1与A1A2两种基因型;两种基因型的频率应当与群 体中两种基因的频率相等,也就是会产生比例为p的A1A1,比例为q的 A1A2。 这些合子的均值为:pa+qd; 与群体均值的离差则是:α1 = pa+qd-[a(p-q)+2dpq] = q[a+d(q-p)] 如α=a+d(q-p), α1 = qα 这就是基因A1的平均效应。 可得A2的平均效应为: α2 = - p[a+d(q-p)] =-pα p、q——分别代表群体中显性基因与隐性基 因的频率; a、d——分别代表显性纯合子与杂合子的基 因型值; α1 ——显性基因(在群体中的)平均效应; α2 ——隐性基因的平均效应

3、个体的育种值 个体的某一性状的育种值,等于它在所有位点上的全部基因的平 均效应之和。 >一个位点时,不同基因型的个体育种值如下: 个体 育种值 A1A1 2a1 =2ga A1A2 a1+a2 =a (q-p) A2A2 2a2=-2pa >从多个位点看,个体的育种值则是分别把各个位点的基因平均效应 相加之后再累加在一起。 如:个体A1A1B1B1C1C1的育种值为:2qAaa+2%e+2q6Q6=2ΣqQ; 个体A1A1B1B2C2C2的育种值为:2qAC+(q%)-2Pc% (、Q、分别代表三个位点上基因取代的平均效应;q、%、qc分别代表 三个位点的隐性基因频率)。 20235因此,简而言之,育种值乃是个体的加性基因值 6
2023/5/23 6 3、个体的育种值 个体的某一性状的育种值,等于它在所有位点上的全部基因的平 均效应之和。 ➢一个位点时,不同基因型的个体育种值如下: 个体 育种值 A1A1 2α1 =2qα A1A2 α1+α2 =α(q-p) A2A2 2α2 = -2pα ➢从多个位点看,个体的育种值则是分别把各个位点的基因平均效应 相加之后再累加在一起。 如:个体A1A1B1B1C1C1的育种值为:2qA A+2qB B+2qC C = 2Σq; 个体A1A1B1B2C2C2的育种值为:2qAA+B (qB-pB) - 2pC C (A、B、C分别代表三个位点上基因取代的平均效应;qA、qB、qC分别代表 三个位点的隐性基因频率)。 因此,简而言之,育种值乃是个体的加性基因值

4、育种值分类 (1)估计育种值 育种值不能直接度量,能够知道的只是个体的表型值。因此通过表 型值和个个体间的亲缘关系来对育种值进行估计,由此得到的估计值即 为估计育种值(estimate breeding value,EBV)。 (2)相对育种值:在实际育种中,为方便比较个体育种值的相对大小,需 要计算出个体的相对育种值(Relative breeding value)。 RBV =(1+ (3)综合育种值 在多性状选择中,要综合考虑不同的性状,因此,根据不同性状在 育种上和经济上的不同重要性差异,用一加权值表示其在经济上的相对 重要性,对各性状加权后的育种值合并,即为综合育种值(total breeding value)。 n n目标性状个数 H=∑o,a,=o'a ω经济加权值 2023/5/23 i=1 a性状的育种值
2023/5/23 7 4、育种值分类 (1)估计育种值 育种值不能直接度量,能够知道的只是个体的表型值。因此通过表 型值和个个体间的亲缘关系来对育种值进行估计,由此得到的估计值即 为估计育种值(estimate breeding value, EBV)。 (2)相对育种值:在实际育种中,为方便比较个体育种值的相对大小,需 要计算出个体的相对育种值(Relative breeding value)。 (1 ) P A RBV = + (3)综合育种值 在多性状选择中,要综合考虑不同的性状,因此,根据不同性状在 育种上和经济上的不同重要性差异,用一加权值表示其在经济上的相对 重要性,对各性状加权后的育种值合并,即为综合育种值(total breeding value)。 = = = n i 1 H i i n 目标性状个数 ω经济加权值 α性状的育种值

二、预测育种值的原理和遗传信息来源 动物育种中,人们总希望选择那些具有尽可能高的一般育种值的个体 作为发展下一世代的亲本种畜。这是因为后代的平均生产成绩水平在很大 程度上依赖于父母的一般育种值。 然而,动物育种值无法直接测量,必须根据性状表型值预测之。 根据回归原理,以被选性状的表型值(P)为自变量,育种值(A)为应 变量;根据P=A+R的分析,在一个大群体中,各种偏差(显性偏差、上位 偏差、环境偏差)正负抵消,平均表型值(P)可以代表平均育种值() A=P+bp(P-P) 2023/5/23 8
2023/5/23 8 二、预测育种值的原理和遗传信息来源 动物育种中,人们总希望选择那些具有尽可能高的一般育种值的个体 作为发展下一世代的亲本种畜。这是因为后代的平均生产成绩水平在很大 程度上依赖于父母的一般育种值。 然而,动物育种值无法直接测量,必须根据性状表型值预测之。 根据回归原理,以被选性状的表型值(P)为自变量,育种值(A)为应 变量;根据P=A+R的分析,在一个大群体中,各种偏差(显性偏差、上位 偏差、环境偏差)正负抵消,平均表型值(P)可以代表平均育种值(A)。 A P b (P P) = + AP -

当根据个体一次记录预测育种值时,育种值对表型值的回归系数b为 SPe-∑(A-AP-P SSP SSP ∑(A-A)(A-A)+(R-】 (.·P=A+R) SSP ∑(A-A)2+∑(A-A(R-R)_∑(A-A)2 SSP .r4R=0) SSP SSA= SSp =h2 A=P+(P-P)h2 预测个体育种值所依据的资料有四种:本身记录、祖先记录、同胞记 录和后裔记录 2023/5/23
2023/5/23 9 当根据个体一次记录预测育种值时,育种值对表型值的回归系数bAP为 b SP SS A A P P SS A A A A R R SS P A R A A A A R R SS A A SS r SS SS h AP AP P P P P P AR A P A P = = − − = − − + − = + = − + − − = − = = = = ( )( ) ( )[( ) ( )] ( ) ( ) ( )( ) ( ) ( ) 2 2 2 2 2 0 A = P + (P - P)h 2 预测个体育种值所依据的资料有四种:本身记录、祖先记录、同胞记 录和后裔记录
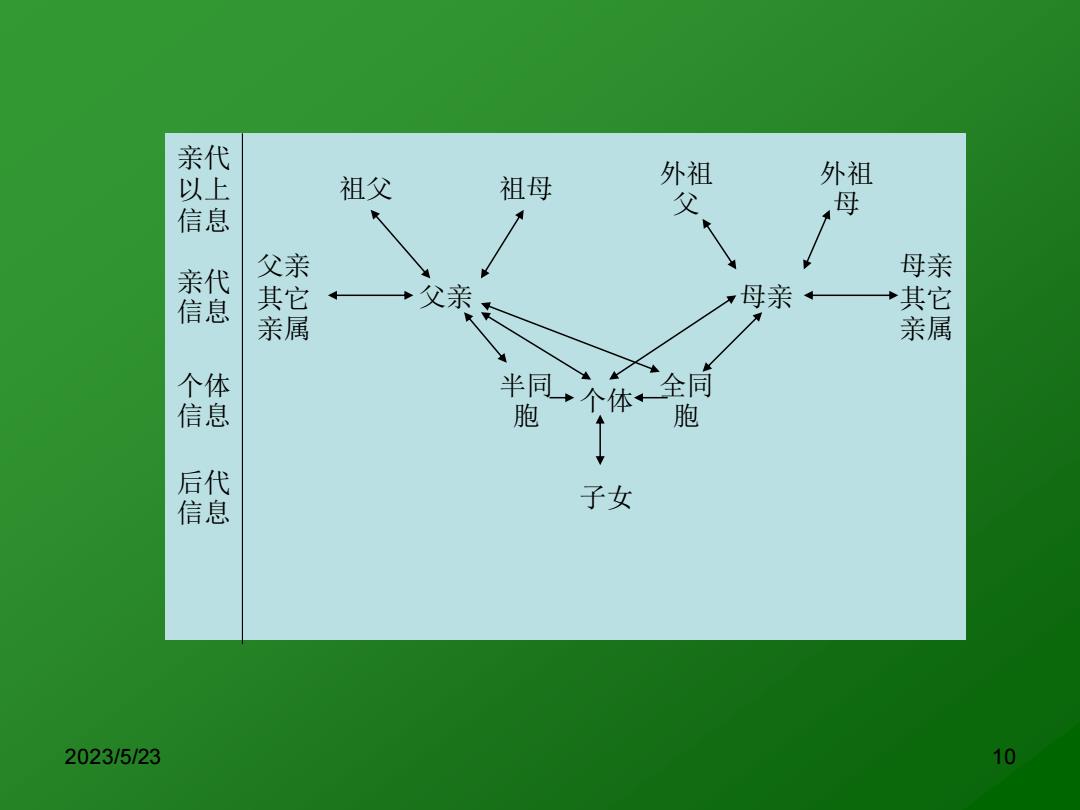
亲 以上 祖父 祖母 外祖 外祖 信息 父 母 亲 父亲 母亲 信息 其它 一父亲 母亲 其它 亲属 个体 信息 半同,个体全同 胞 后代 信息 子女 2023/5/23 10
2023/5/23 10 亲代 以上 信息 祖父 祖母 外祖 父 外祖 母 亲代 信息 父亲 其它 亲属 父亲 母亲 母亲 其它 亲属 个体 信息 半同 胞 个体 全同 胞 后代 信息 子女