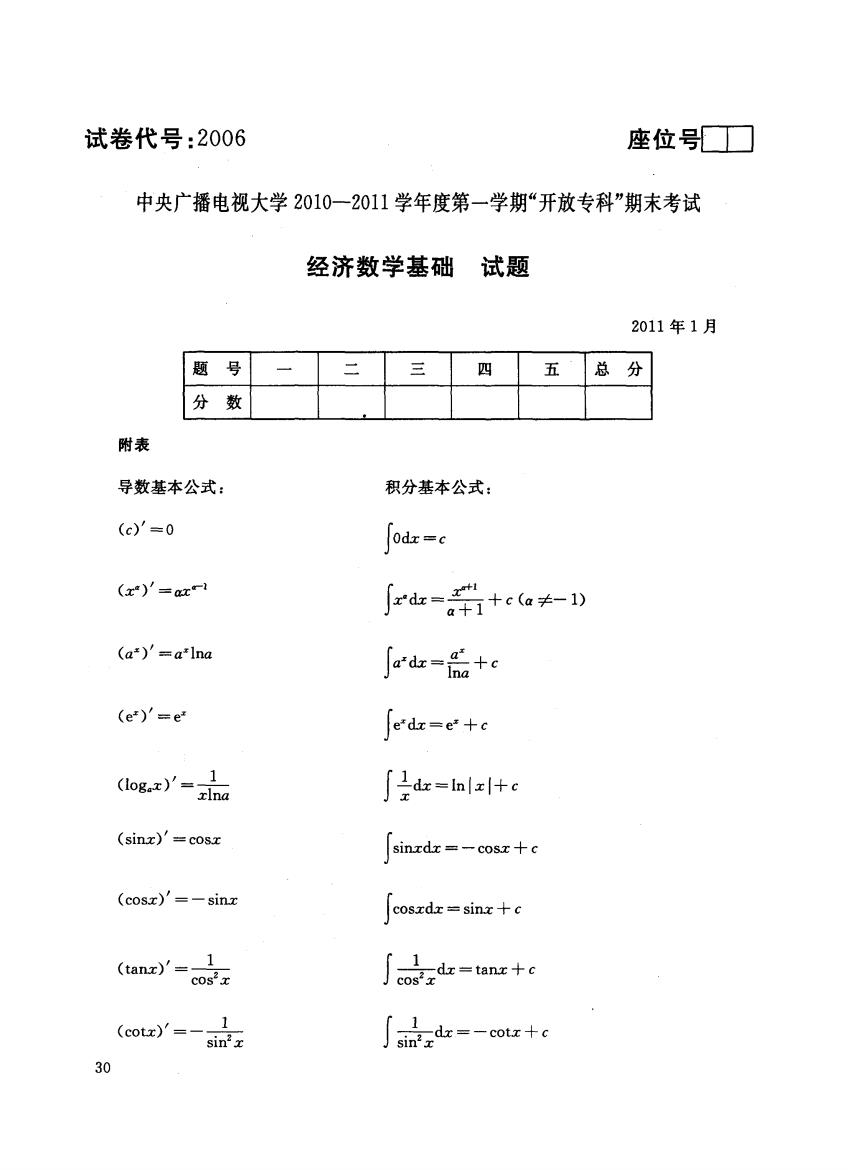
试卷代号:2006 座位口 中央广播电视大学2010一2011学年度第一学期“开放专科”期末考试 经济数学基础 试题 2011年1月 题号 一 二 三 四 五 总分 分 数 附表 导数基本公式: 积分基本公式: (c)'=0 [odz-c (x)'=ax-1 ∫rd=+eo-) (a*)'=a*Ina jrdk=品+c (e)'=e* e'dx=e*+c (log.)'=-1 xlna ∫dk=linl+c (sinz)'=cosx sinxdx=-cosx+c (cosx)'=-sinx cosxdx=sinx++c (tanz)'=-1 s2x [-1-dx=tanz+c (cotz)=- 1 sin'x sinda--cot+c 1 30
试卷代号 0 0 座位号IT] 中央广播电视大学 11学年度第一学期"开放专科"期未考试 经济数学基础试题 2011 年1 |题号|一|二|三|四|五|总分| |分数 I. I I I I I 附表 导数基本公式 权分基本公式: (C)' =0 (x αx.- +! =1= 1) 十1 (a =arlna rdx= Ina (e =eZ e'" e"'+c (iogaxYz 1 I z-由Ix = ln lx xlna (sinx)' = cosx Isinxdx=一cosx+c (cosx)' = - sinx I cosxdx = sinx (tanx)' =~1 !.-dx=tar 十C COSZx COSZx (cotx)' 1 .1 dz=-cotz+C sinzx sinzx 30

得分 评卷人 一、单项选择题(每小题3分,本题共15分) 1.下列函数中为奇函数的是( A.y=x2-x B.y=e*+e C.y=I x+1 D.y=xsinx 2.设需求量q对价格p的函数为g()=3一2√p,则需求弹性为E。=(). A. B. 3-2y匝 3-2√p √p C.-3-2E D. √p 3-2√p 3.下列无穷积分中收敛的是( A.eds J。 D.nadz 4.设A为3×2矩阵,B为2×3矩阵,则下列运算中( )可以进行. A.AB B.A+B C.ABT D.BAT 5.线性方程组 x1十x2=1 解的情况是( ). x1+x2=0 A.有唯一解 B.只有0解 C.有无穷多解 D.无解 得 分 评卷人 二、填空题(每小题3分,共15分) 6.函数f(x)=一4 x-2 的定义域是 7.函数f()=1。的间断点是 8.若f(x)dr=F(x)十c,则ef(e)dx= 0.21 9.设A=a0 3 ,当a= 时,A是对称矩阵, 23-1 10.若线性方程组 x1一x2=0 有非零解,则入= x1十x2=0 31
|得分|评卷人| I j I 一、单项选择题{每小题 3分,本题共 5分} 3· B. y=ex + e-x D. y=xsinx 2. 求量 .[p = ( ). A. .jp B.主二 ../ .[p $ c. .jp D. $ 3-2.[p 3. 无穷 ). r~ r斗 A. I ~~ B. I 4~ JO Jl X r+oo 1 r+o c. D. I lnxdx Jl .::Ix J 4. 设A 为3X2 ,B 为2X3 矩阵 运算 )可以进行. A.AB B. C. ABT D. BAT (Xl +x. =1 5. -0 况是 ). [Xl +X2 =0 A.有唯一解 .只有 O解 C. 解D. |得分|评卷人| I I I 二、填空题{每小题 3分,共 5分} ,则叫 2 1 9. la 0 3 I ,当 =一一一一一时 A是对称矩阵. IXI =v 10. 性方 { ' "有非零解,则J. lXl + Ax 2 =0 31

得分 评卷人 三、微积分计算题(每小题10分,共20分) 11.设y=32+cos5x,求dy. 12.计算定积分 xlnxdx. 得分 评卷人 四、线性代数计算题(每小题15分,共30分) 07 ro 17 13.设矩阵A= 0 -1 ,B= 0 ,求(BTA)1. L-1 2 12 x1+2x3一x4=0 14.求齐次线性方程组 一x1十x2一3x3十2x4=0的一般解. 2x1-x2+5x3-3x4=0 得 分 评卷人 五、应用题(本题20分) 15.生产某产品的总成本为C(x)=3十x(万元),其中x为产量,单位:百吨.边际收入为 R'(x)=15一2x(万元/百吨),求: (1)利润最大时的产量; (2)从利润最大时的产量再生产1百吨,利润有什么变化? 32
|得分|评卷人| I I I 三、微积分计算题{每小题 0分,共 0分} 1. = 3'" + COgS X 12 算定积分 J:xlnx |得分|评卷人| 算题{每小题 5分,共 0分} I I I fXI +2 =0 14. 求齐 性方程组 +xz-3岛+2x. =0 l2xI - Xz + 5xg |得分|评卷人| I I I 五、应用题{本题 0分} 15. 产某 =3 +X ,其中 z为产量,单位z百吨.边际收入为 R' (X) = 15 - 2x 百吨 ,求 (1)利润最大时的产量 (2) 利润最大 量再 产1 变化 32

试卷代号:2006 中央广播电视大学2010一2011学年度第一学期“开放专科”期末考试 经济数学基础 试题答案及评分标准 (供参考) 2011年1月 一、单项选择题(每小题3分,本题共15分) 1.C 2.D 3.B 4.A 5.D 二、填空题(每小题3分,本题共15分) 6.(-∞,-2]U(2,+∞) 7.x=0 8.-F(er)+c 9.0 10.1 三、微积分计算题(每小题10分,共20分)】 11.解:由徽分运算法则和徽分基本公式得 dy=d(3=+cossx)=d(3*)+d(cossx) =3*In3dx+5 cos'xd(cosx) =3*In3dx-5sinx cos'xdx =(3ln3-5 sinx c0sx)dx……10分 12.解:由分部积分法得 d=ari-∫rdnx) =号-∫八x=号+号 10分 33
试卷代号 中央广播电视大学 2 0 11学年度第一学期"开放专科"期末考试 经济数学基础试题答案及评分标准 (供参考) 2011 年1 -、单项选择题{每小题 3分,本题共 5分} I. e 2.0 3.B 4.A 5.0 二、填空题{每小题3分,本题共 5分} 6. (一∞,一 U(2 , +∞) 7. x=O 8. - F(e-"') +c 9. 0 10. 一1 三、微积分计算题{每小题 0分,共 0分} 11. 运算 微分基本公式 dy = d(3'" +cossx) = d(3 d(cosS x) = 3"'ln3dx+5 cos 4 xd(cosx) = 3"'ln3dx - 5sinx cos4 xdx = (3"'ln3 - 5sinx cos4 x)dx ……………… …………… … … … … 12. 积分 f: nxdx 专f>2 =Ei-l|ezdz= -H·H·-….........................................….. 10 2 2 J1-- 4' 4 33

四、线性代数计算题(每小题15分,共30分)】 13.解:因为 0 -H 8分 2 所以由公式可得 …15分 14.解:因为系数矩阵 「1 02 -17 0 2 17 A= -1 1 -3 2 0 1 -1 1 2 -1 5 -3 -11-1 10 2 -17 01-1 1 …10分 0.00 0 x1=-2x3十x4 所以一般解为 (其中x3,x4是自由未知量)…15分 x2=xg一x4 五、应用题(本题20分) 15.解:(1)因为边际成本C(x)=1,边际利润 L'(x)=R'(x)-C(x) =15-2x-1=14-2x 令L'(x)=0得x=7(百吨) 又x=7是L(x)的唯一驻点,根据问题的实际意义可知L(x)存在最大值,故x=7是 L(x)的最大值点,即当产量为7(百吨)时,利润最大.…10分 (2)L=)L'(x)dz=i(14-2x)d =14x-x2):=-1 即从利润最大时的产量再生产1百吨,利润将减少1万元.…20分 34
四、线性代数计算题{每小题 5分,共 0分} 13. 'EA'EA H-MIL mtlLU BTA Ed -- qu'i fl 0 2 A= 1-1 1 -3 I 2 -1 5 JjtJ JJ| fl0 2 -11 • 10 1 -1 1 I 0 0 . 10 (Xl +X4 所以一般解为~ (其中岛,且是自由未知量〉…….....•. •.. .....….. 15 lX2 =岛 五、应用题{本题 0分} 15. (1)因为边际成本 1,边际利润 L'(x) =R' (x) 一c'(x) =15 - 2x-l=14-2x =0 得x=7( 一驻 实际意 可知 L(x) 即 当 利润 . . . . . . . . . . . . . . . . . . . . 10 (川 f: L'(x)dx = f: (1 4 =ω I: =-1 即从利润最大时的产量再生产1百吨,利润将减少1万元..........................….20 34