
The second Law of Thermodynamics 熟力学第二定律 西安科技大学北学与北工系 Xi an University of Science Technology
热力学第二定律 The second Law of Thermodynamics 西安科技大学化学与化工系 Xi’an University of Science & Technology

2.1 自发变化的共同特征 热大 自发变化某种变化有自动发生的趋势,一旦发生就无需借助 外力,可以自动进行,这种变化称为自发变化。 自发变化的共同特征一不可逆性任何自发变化的逆过程是不 能自动进行的。例如: (1) 焦耳热功当量中功自动转变成热; (2) 气体向真空膨胀; (3) 热量从高温物体传入低温物体; (4) 浓度不等的溶液混合均匀; (5) 锌片与硫酸铜的置换反应等, 它们的逆过程都不能自动进行。当借助外力,体系恢复原状后, 会给环境留下不可磨灭的影响
Xi’an University of science & Technology 2.1 自发变化的共同特征 自发变化 某种变化有自动发生的趋势,一旦发生就无需借助 外力,可以自动进行,这种变化称为自发变化。 自发变化的共同特征—不可逆性 任何自发变化的逆过程是不 能自动进行的。例如: (1) 焦耳热功当量中功自动转变成热; (2) 气体向真空膨胀; (3) 热量从高温物体传入低温物体; (4) 浓度不等的溶液混合均匀; (5) 锌片与硫酸铜的置换反应等, 它们的逆过程都不能自动进行。当借助外力,体系恢复原状后, 会给环境留下不可磨灭的影响

过程方向的共同判据 过程推动力=一△B(系) 过程反抗力=△B(环) 净推动力=一△B(系)一△B(环) >0能自动进行 0可逆 0不可能自动进行 一个过程能否按指定方向自动进行,取决于是否有推动此过程进行的净推动 力。即过程自动进行,则系统与环境总的做功能力一定减少;反之,则不能 自动进行
过程方向的共同判据 Xi’an University of science & Technology 过程推动力=-△B(系) 过程反抗力= △B (环) 净推动力=-△B(系)-△B(环) > 0 能自动进行 = 0 可逆 < 0 不可能自动进行 隔离系统的做功能力变化用△B(隔)表示 △B(隔)=△B(环)+△B(系)则 △B(隔)< 0 能自动进行 = 0 可逆 > 0 不可能自动进行 一个过程能否按指定方向自动进行,取决于是否有推动此过程进行的净推动 力。即过程自动进行,则系统与环境总的做功能力一定减少;反之,则不能 自动进行

热力学第二定律 (The Second Law of Thermodynamics) 克势渗其情说是 ●不可籠泡热量观佩温杨体传到高温杨体 希不机是男@或他
Xi’an University of science & Technology 热力学第二定律 (The Second Law of Thermodynamics)

热力学第二定律 (The Second Law of Thermodynamics) 开尔永说法 不可都从单一熟原围热逆之完至 变为切不3思男它3变图 武或第二类永动W机是因不成的
Xi’an University of science & Technology 热力学第二定律 (The Second Law of Thermodynamics)

卡诺循环与卡诺定理 。卡诺循环 •热机效率 ●卡诺定理
卡诺循环与卡诺定理 Xi’an University of science & Technology •卡诺循环 •热机效率 •卡诺定理

卡诺循环(Carnot cycle) 1824年,法国工程师 高温存储器 N.L.S.Carnot(1796~1832)设计 了一个循环,以理想气体为 工作物质,从高温(红热源吸 热机 收Q的热量,一部分通过理 想热机用来对外做功W,另一 部分Q的热量放给低温(工)热 源。这种循环称为卡诺循环。 低温存储器 卡诺循环
卡诺循环( Xi’an University of science & Technology Carnot cycle) 1824 年,法国工程师 N.L.S.Carnot (1796~1832)设计 了一个循环,以理想气体为 工作物质,从高温 热源吸 收 的热量,一部分通过理 想热机用来对外做功W,另一 部分 的热量放给低温 热 源。这种循环称为卡诺循环。 ( ) Th Qh Qc ( ) Tc

卡诺循环(Carnot cycle) 1mol理想气体的卡诺循环在pV图上可以分为四步: 过程1:等温(T)可逆膨胀由p,到p,'(A→B) △U,=0 所=-Rrng Q,=-W 所作功如AB曲线下的面积所示。 A(piVi) Q B(D2V2) 卡诺循环第一步
卡诺循环( Xi’an University of science & Technology Carnot cycle) 1mol 理想气体的卡诺循环在pV图上可以分为四步: 过程1:等温 ( ) Th 可逆膨胀由 p1 V1 到 (A B) p2 V2 → U1 = 0 2 1 h 1 lnV W nRT V = − 所作功如AB曲线下的面积所示。 Q W h 1 = −
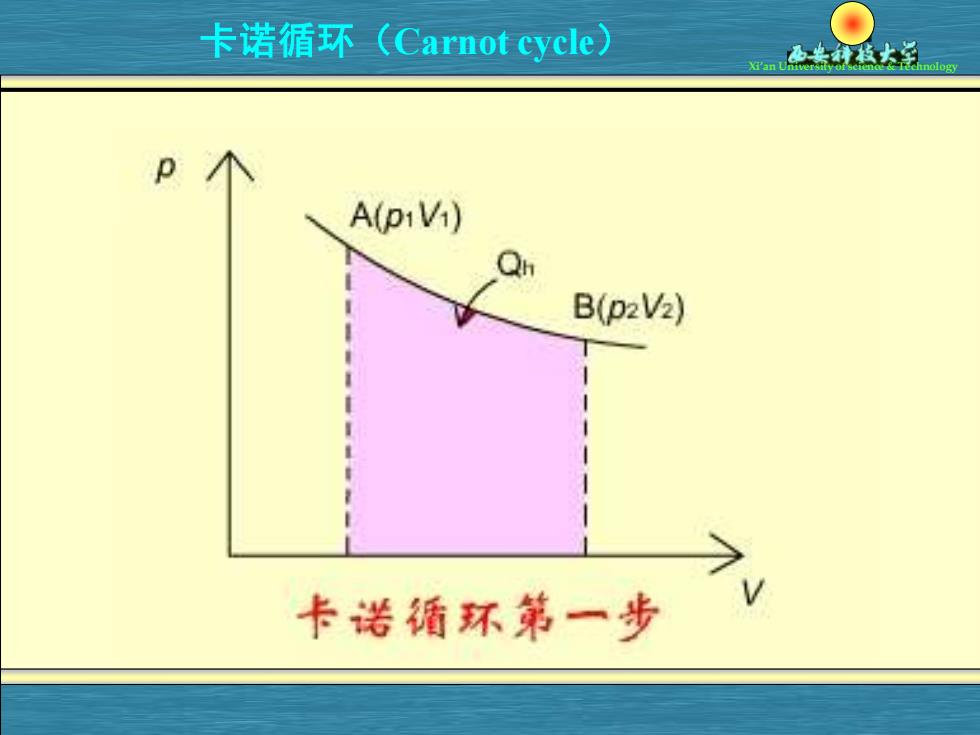
卡诺循环(Carnot cycle) A(piVi) B(p2V2) 卡诺循环第一步
卡诺循环( Xi’an University of science & Technology Carnot cycle)
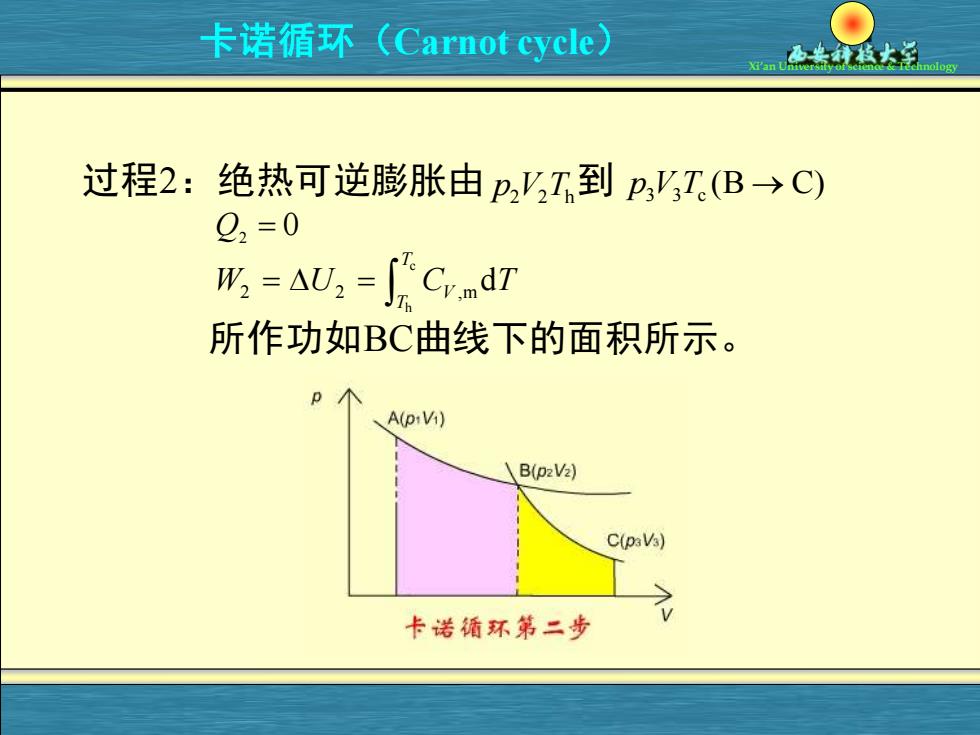
卡诺循环(Carnot cycle) 过程2:绝热可逆膨胀由p,I到p,'T(B→C) Q2=0 形=aU,=Cndr 所作功如BC曲线下的面积所示。 A(p:Vi) \B(p2V2) C(paVs) 卡诺循环第二步
卡诺循环( Xi’an University of science & Technology Carnot cycle) 过程2:绝热可逆膨胀由 p V T 2 2 h 到 3 3 c p V T (B C) → Q2 = 0 c h 2 2 ,md T V T W U C T = = 所作功如BC曲线下的面积所示