
CHAPTER 24 TIME INCONSISTENCY AND HEALTH
CHAPTER 24 TIME INCONSISTENCY AND HEALTH
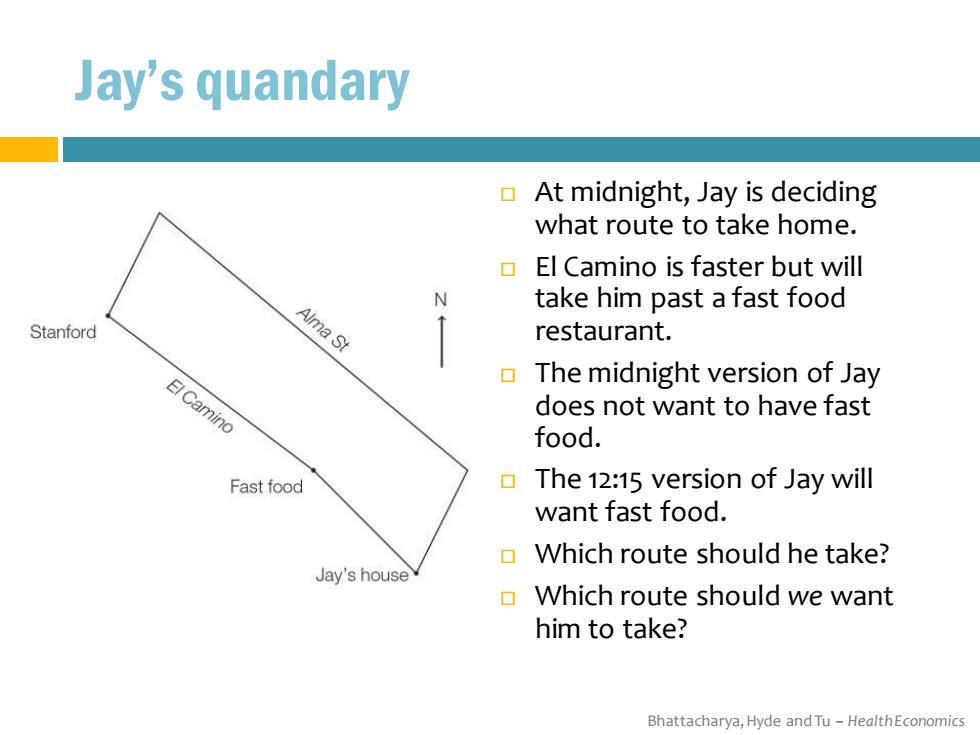
Jay's quandary At midnight,Jay is deciding what route to take home. El Camino is faster but will N take him past a fast food Stanford Alma St restaurant. The midnight version of Jay E日Camino does not want to have fast food. Fast food The 12:15 version of Jay will want fast food. Which route should he take? Jay's house Which route should we want him to take? Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Jay’s quandary At midnight, Jay is deciding what route to take home. El Camino is faster but will take him past a fast food restaurant. The midnight version of Jay does not want to have fast food. The 12:15 version of Jay will want fast food. Which route should he take? Which route should we want him to take?

THE BETA-DELTA DISCOUNTING MODEL Chapter 24:Time inconsistency and health
Chapter 24: Time inconsistency and health THE BETA-DELTA DISCOUNTING MODEL

Beta-delta discounting Individuals derive utility not only from present joys but also from the anticipation of future happiness. People do not maximize simply their instantaneous utility levels but rather some function of present and future utility. This is why we pay now for tickets to concerts months in advance and get flu vaccinations that will not pay off until flu season. Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Beta-delta discounting Individuals derive utility not only from present joys but also from the anticipation of future happiness. People do not maximize simply their instantaneous utility levels but rather some function of present and future utility. This is why we pay now for tickets to concerts months in advance and get flu vaccinations that will not pay off until flu season

Beta-delta discounting To account for this fact,economists model overall utility as a weighted sum of instantaneous utility levels from the present period and all future periods: Uoverall=aloday+bUtomorrow+CUthe mext day+··, The coefficients a,b and c are weights that represent the fact that individuals do not necessarily value utility in all periods equally. People value utility now more than utility later. ·Thus a>b>c Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics To account for this fact, economists model overall utility as a weighted sum of instantaneous utility levels from the present period and all future periods: Uoverall = aUtoday + bUtomorrow + cUthe next day + · · · • The coefficients a, b and c are weights that represent the fact that individuals do not necessarily value utility in all periods equally. • People value utility now more than utility later. • Thus a > b > c Beta-delta discounting

Beta-delta discounting The vector of weights fa,b,c,...is called a discounting function. Discounting function:a vector of weights that indicates how much an individual values utility in present and future periods. In theory,one's discounting function could take any shape,but in general,economists who study time inconsistency assume that discounting functions are monotonically decreasing and reasonably approximated with just two parameters. Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics The vector of weights {a, b, c, . . . } is called a discounting function. Discounting function: a vector of weights that indicates how much an individual values utility in present and future periods. In theory, one’s discounting function could take any shape, but in general, economists who study time inconsistency assume that discounting functions are monotonically decreasing and reasonably approximated with just two parameters. Beta-delta discounting

The beta-delta discounting model With beta-delta discounting,a discounting function can be specified by two parameters,B and 8,where o ≤B≤1and0<δ≤1. Overall utility is the sum of instantaneous utility from period o and is given by the following equation: Uoverall=Uo+B [8U1 +82U2+..] where: B is the present bias parameter that discounts utility in all non-current periods,and 6 is the discount rate parameter that discounts utility incrementally more in each subsequent period. Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics With beta-delta discounting, a discounting function can be specified by two parameters, β and δ, where 0 ≤ β ≤ 1 and 0 < δ ≤ 1. Overall utility is the sum of instantaneous utility from period 0 and is given by the following equation: Uoverall = U0 + β [δ1U1 +δ2U2 +···] where: Β is the present bias parameter that discounts utility in all non-current periods, and δ is the discount rate parameter that discounts utility incrementally more in each subsequent period. The beta-delta discounting model

The beta-delta discounting model o Likeδ,βis assumed to range between o and1. The term B is absent from the first term in the equation but present in all other terms. This means that utility from any future period receives an extra devaluation. Alternatively,we could say that utility in the present is valued especially highly,even more highly than it would be based on the discount rate alone. This is what is meant by present bias. The closer it is to zero,the more future utility is discounted and the greater the bias toward the present. Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Like δ , β is assumed to range between 0 and 1. The term β is absent from the first term in the equation but present in all other terms. This means that utility from any future period receives an extra devaluation. Alternatively, we could say that utility in the present is valued especially highly, even more highly than it would be based on the discount rate alone. This is what is meant by present bias. The closer it is to zero, the more future utility is discounted and the greater the bias toward the present. The beta-delta discounting model

TIME-CONSISTENT PREFERENCES Chapter 24:Time inconsistency and health
Chapter 24: Time inconsistency and health TIME-CONSISTENT PREFERENCES

Time-consistent preferences The traditional way of modeling time preference assumes that people are time-consistent in their preferences. Time-consistent preferences:Preferences shared across all selves,so that future selves will not alter a plan that a previous self found optimal. Within the beta-delta model,preferences are time-consistent if,and only if,B=1. If B=1,the resulting utility function is said to exhibit exponential discounting because utility from period t is worth 6t as much as utility in the current period. Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Time-consistent preferences The traditional way of modeling time preference assumes that people are time-consistent in their preferences. Time-consistent preferences: Preferences shared across all selves, so that future selves will not alter a plan that a previous self found optimal. Within the beta-delta model, preferences are time-consistent if, and only if, β = 1. If β = 1, the resulting utility function is said to exhibit exponential discounting because utility from period t is worth δt as much as utility in the current period