
CHAPTER 7 DEMAND FOR INSURANCE
CHAPTER 7 DEMAND FOR INSURANCE

Why buy insurance? Demand for insurance driven by the fear of the unknown Hedge against risk--the possibility of bad outcomes Purchasing insurance means forfeiting income in good times to get money in bad times If bad times avoided,then money lost Ex:The individual who buys health insurance but never visits the hospital might have been better off spending that income elsewhere. Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Why buy insurance? Demand for insurance driven by the fear of the unknown Hedge against risk -- the possibility of bad outcomes Purchasing insurance means forfeiting income in good times to get money in bad times If bad times avoided, then money lost Ex: The individual who buys health insurance but never visits the hospital might have been better off spending that income elsewhere

Risk aversion Hence,risk aversion drives demand for insurance We can model risk aversion through utility from income U(I) Utility increases with income:U'(1)>o Marginal utility for income is declining:U"(1)<o Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Risk aversion Hence, risk aversion drives demand for insurance We can model risk aversion through utility from income U(I) Utility increases with income: U(I) > 0 Marginal utility for income is declining: U(I) < 0
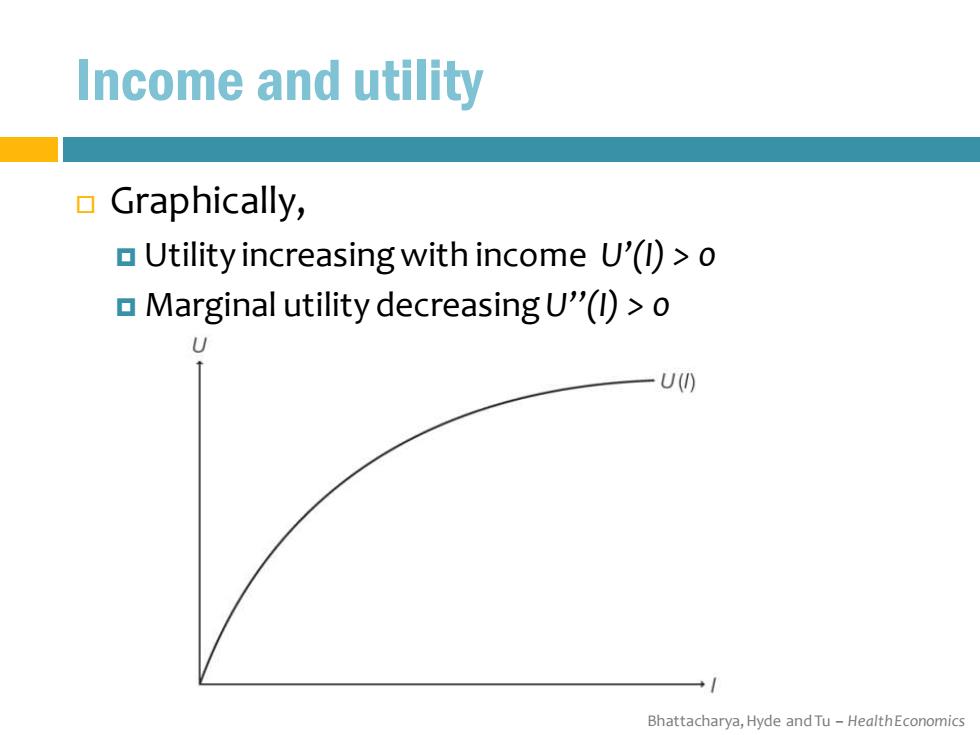
Income and utility Graphically, Utility increasing with income U'(l)>o Marginal utility decreasing U"(1)>o U() → Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Income and utility Graphically, Utility increasing with income U’(I) > 0 Marginal utility decreasing U’’(I) > 0

Adding uncertainty to the model An individual does not know whether she will become sick,but she knows the probability of sickness is p between o and 1 Probability of sickness is p Probability of staying healthy is 1-p If she gets sick,medical bills and missed work will reduce her income Is=income if she does get sick IH>Is=income if she remains healthy Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Adding uncertainty to the model An individual does not know whether she will become sick, but she knows the probability of sickness is p between 0 and 1 Probability of sickness is p Probability of staying healthy is 1 - p If she gets sick, medical bills and missed work will reduce her income IS = income if she does get sick IH > IS = income if she remains healthy

Expected value The expected value of a random variable X,E[X],is the sum of all the possible outcomes of X weighted by each outcome's probability If the outcomes are x,x2,...,n,and the probabilities for each outcome are p1,p2,...,Pn respectively,then: E[X]=PX+p2X2+..+Pn Xn In our individual's case,the formula for expected value of income E[l]: [叮=pls+(1p)lH Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Expected value The expected value of a random variable X, E[X], is the sum of all the possible outcomes of X weighted by each outcome’s probability If the outcomes are x1 , x2 , . . . , xn , and the probabilities for each outcome are p1, p2 , . . . , pn respectively, then: E[X] = p1 x1 + p2 x2 + · · · + pn xn In our individual’s case, the formula for expected value of income E[I]: E[I] = p IS + (1- p) IH

Example:expected value Suppose we offer a starving graduate student a choice between two possible options,a lottery and a certain payout: A:a lottery that awards $500 with probability o.5 and so with probability o.5. B:a check for $250 with probability 1. The expected value of both the lottery and the certain payout is $250: E[I]=pIs+(1-p)I E[A]=.5(500)+.5(o)=$250 E[B]=1(250)=250 Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Example: expected value Suppose we offer a starving graduate student a choice between two possible options, a lottery and a certain payout: A: a lottery that awards $500 with probability 0.5 and $0 with probability 0.5. B: a check for $250 with probability 1. The expected value of both the lottery and the certain payout is $250: E[I] = p IS + (1- p) IH E[A] = .5(500) + .5(0) = $250 E[B] = 1(250) = $250

People prefer certain outcomes Studies find that most people prefer certain payouts over uncertain scenarios If a student says he prefers uncertain option, what does that imply about his utility function? To answer this question,we need to define expected utility for a lottery or uncertain outcome. Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics People prefer certain outcomes Studies find that most people prefer certain payouts over uncertain scenarios If a student says he prefers uncertain option, what does that imply about his utility function? To answer this question, we need to define expected utility for a lottery or uncertain outcome

Expected Utility The expected utility from a random payout X E[U(X)]is the sum of the utility from each of the possible outcomes,weighted by each outcome's probability. If the outcomes are x,X2,...,Xn,and the probabilities for each outcome are p,,P2,...,Pn respectively,then: ▣E[U(X)]=PU(x)+P2U(x2)+·+PnU(xn) Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Expected Utility The expected utility from a random payout X E[U(X)]is the sum of the utility from each of the possible outcomes, weighted by each outcome’s probability. If the outcomes are x1 , x2 , . . . , xn , and the probabilities for each outcome are p1 , p2 , . . . , pn respectively, then: E[U(X)] = p1 U(x1 ) + p2 U(x2 ) + · · · + pn U(xn )

Example The student's preference for option B over option A implies that his expected utility from B,is greater than his expected utility from A: E[U(B)]≥E[U(A)] U(525o)20.5U(500)+0.5U(50) In this case,even though the expected values of both options are equal,the student prefers the certain payout over the less certain one. This student is acting in a risk-averse manner over the choices available. Bhattacharya,Hyde and Tu-HealthEconomics
Bhattacharya, Hyde and Tu – Health Economics Example The student’s preference for option B over option A implies that his expected utility from B, is greater than his expected utility from A: E[U(B)] ≥ E[U(A)] U($250) ≥ 0.5 U($500) + 0.5 U($0) In this case, even though the expected values of both options are equal, the student prefers the certain payout over the less certain one. This student is acting in a risk-averse manner over the choices available