
第四章线性控制系统的 稳定性和稳态误差 4.1线性象统稳定性的基本概念 4.2传递函数表示的条统稳定性判定 4.3线性系统稳态误差的计算 4.4本章小结 2023/724 北京料技大学自动化学院自功化系
2023/7/24 北京科技大学自动化学院自动化系 1 第四章 线性控制系统的 稳定性和稳态误差 4.1 线性系统稳定性的基本概念 4.2 传递函数表示的系统稳定性判定 4.3线性系统稳态误差的计算 4.4 本章小结

4.1线性系统稳定性的基本概念 一、稳定性分析的重要性 稳定是控制条统能够正常运行的首要条件 对系统进行各类品质指标的分析必须在系统 稳定的前提下进行。 自动控制理论的基本任务(之一) 分析象统的稳定性问题 提出保证朱统稳定的措施 2023/724 北京料技大学自动化学院自功化系 2
2023/7/24 北京科技大学自动化学院自动化系 2 稳定是控制系统能够正常运行的首要条件 ►对系统进行各类品质指标的分析必须在系统 稳定的 前提下进行。 自动控制理论的基本任务(之一) ► 分析系统的稳定性问题 ► 提出保证系统稳定的措施 一、稳定性分析的重要性 4.1线性系统稳定性的基本概念
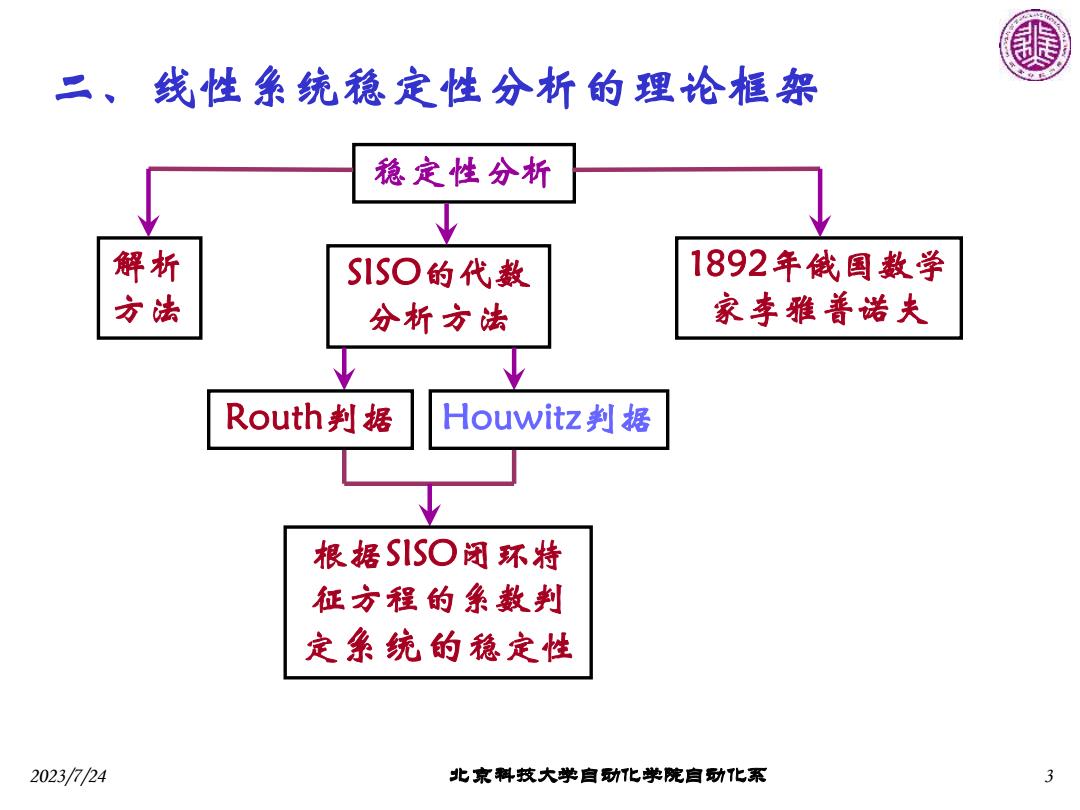
二、线性系统稳定性分析的理论框架 稳定性分析 解析 S1SO的代数 1892年俄国数学 方法 分析方法 家李雅善诺夫 Routh判据 Houwitz判据 根据S1SO闭环特 征方程的条数判 定系统的稳定性 2023/724 北京料技大学自动化学院自功化系 3
2023/7/24 北京科技大学自动化学院自动化系 3 二、线性系统稳定性分析的理论框架 稳定性分析 1892年俄国数学 家李雅普诺夫 SISO的代数 分析方法 解析 方法 Routh判据 Houwitz判据 根据SISO闭环特 征方程的系数判 定系统的稳定性

三、线性系统稳定性分析的划时代人物 A.Lyapunov(1857-1918), 俄国数学家(Chebyshev 的学生,Markov的同学), 在他的博士论文中, Lyapunov条统地研究了由 微分方程描述的一般运动 的稳定性问题,建立了著 名的Laypunov方法,他的 工作为现代控制及非线性 控制真定科基础。 2023/7/24 北京料技大学自动化学院自功化系 4
2023/7/24 北京科技大学自动化学院自动化系 4 A.Lyapunov(1857-1918), 俄国数学家(Chebyshev 的学生,Markov的同学), 在他的博士论文中, Lyapunov系统地研究了由 微分方程描述的一般运动 的稳定性问题,建立了著 名的Laypunov方法,他的 工作为现代控制及非线性 控制奠定科基础。 三、线性系统稳定性分析的划时代人物

4.2传递蹈数表示的系统稳定性半)定 本小节是本章的重点,主要介绍以下内容: 4.2.1S1S○线性定常条统的稳定性问题 4.2.2 Routh稳定判据 4.2.3 Routh判据的两种特殊情况 4.2.4 Routh判据的推广 4.2.5 Routh判据的应用 2023/724 北京料技大学自动化学院自功化系 5
2023/7/24 北京科技大学自动化学院自动化系 5 4.2 传递函数表示的系统稳定性判定 本小节是本章的重点,主要介绍以下内容: 4.2.1 SISO线性定常系统的稳定性问题 4.2.2 Routh稳定判据 4.2.3 Routh判据的两种特殊情况 4.2.4 Routh判据的推广 4.2.5 Routh判据的应用
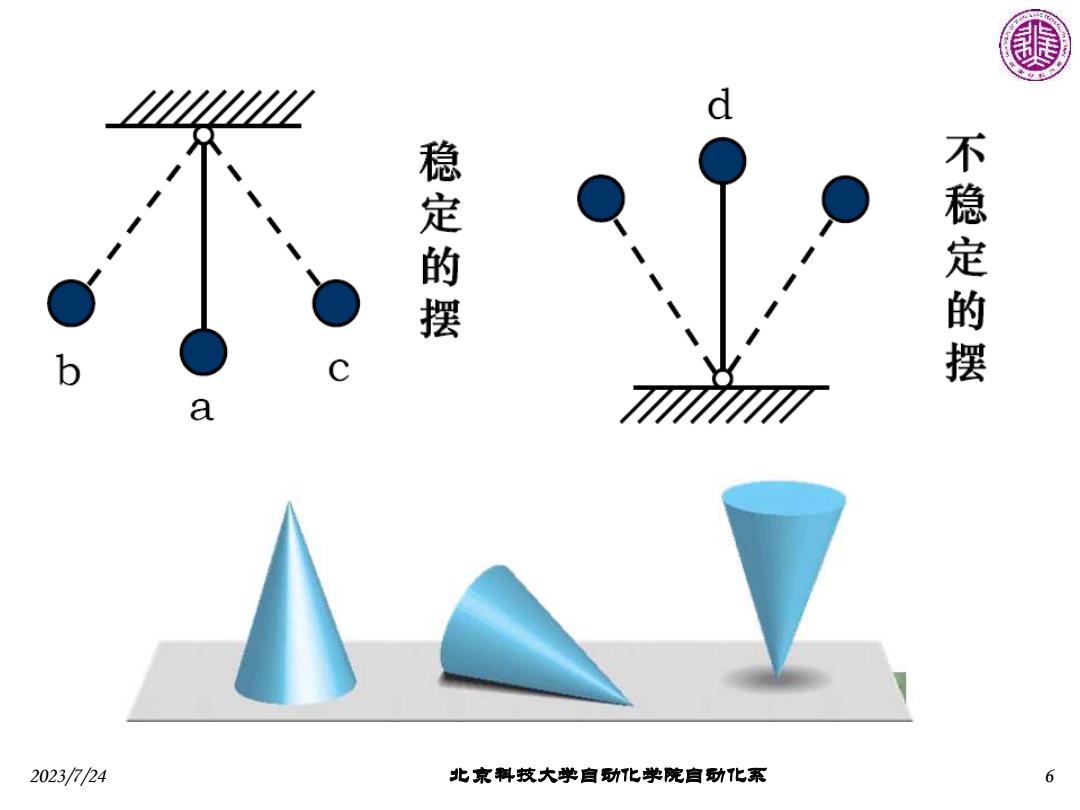
M d 稳定的摆 不稳定的摆 b C a 2023/7/24 北京料技大学自动化学院自功化系 6
2023/7/24 北京科技大学自动化学院自动化系 6

跨越华盛顿州塔科马峡 谷的首座大桥,开通于 1940年7月1日。只要 有风,这座大桥就会晃 动。 1940年11月7日,一 阵风引起了桥的晃动, 而且晃动越来越大,直 到整座桥断裂。 2023/7/24 北京料技大学自动化学院自功化系
2023/7/24 北京科技大学自动化学院自动化系 7
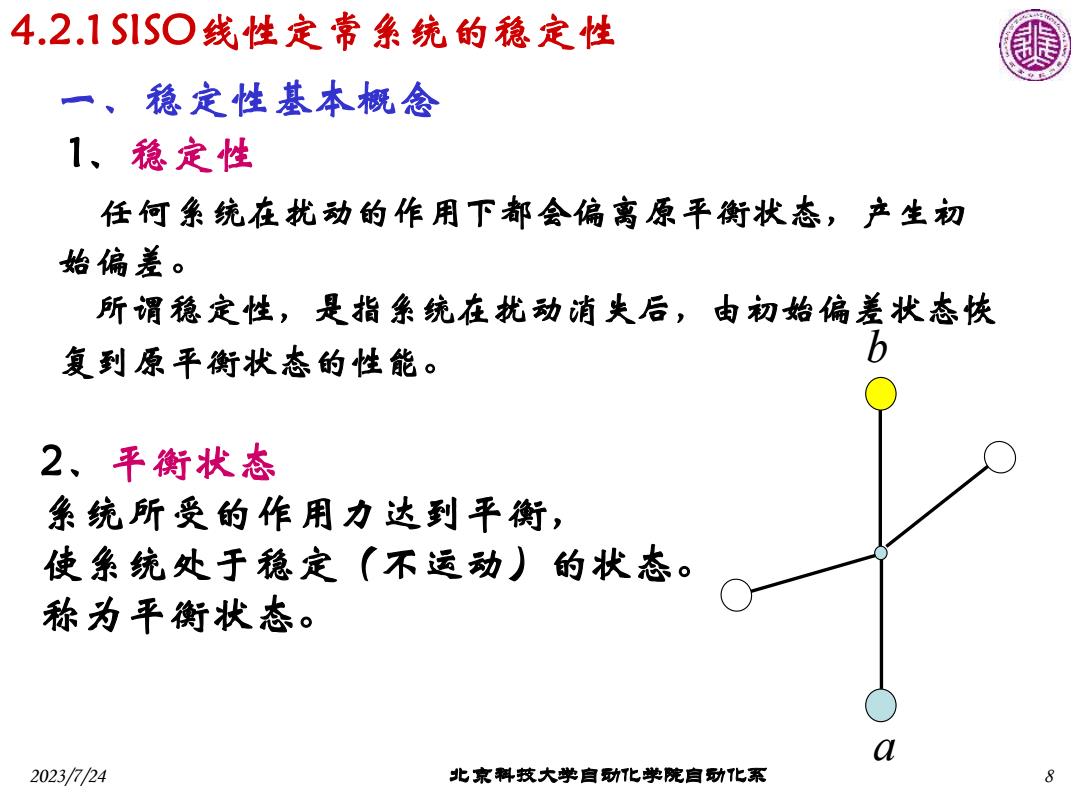
4.2.1S1S○线性定常系统的稳定性 一、稳定性基本概念 1、稳定性 任何系统在扰动的作用下都会偏离原平衡状态,产生初 始偏差。 所谓稳定性,是指系统在扰动消失后,由初始偏差状态恢 复到原平衡状态的性能。 2、平衡状态 系统所受的作用力达到平衡, 使条统处于稳定(不运动)的状态。 称为平衡状态。 a 2023/724 北京料技大学自动化学院自功化系 8
2023/7/24 北京科技大学自动化学院自动化系 8 一、稳定性基本概念 1、稳定性 任何系统在扰动的作用下都会偏离原平衡状态,产生初 始偏差。 所谓稳定性,是指系统在扰动消失后,由初始偏差状态恢 复到原平衡状态的性能。 4.2.1 SISO线性定常系统的稳定性 2、平衡状态 系统所受的作用力达到平衡, 使系统处于稳定(不运动)的状态。 称为平衡状态。 a b
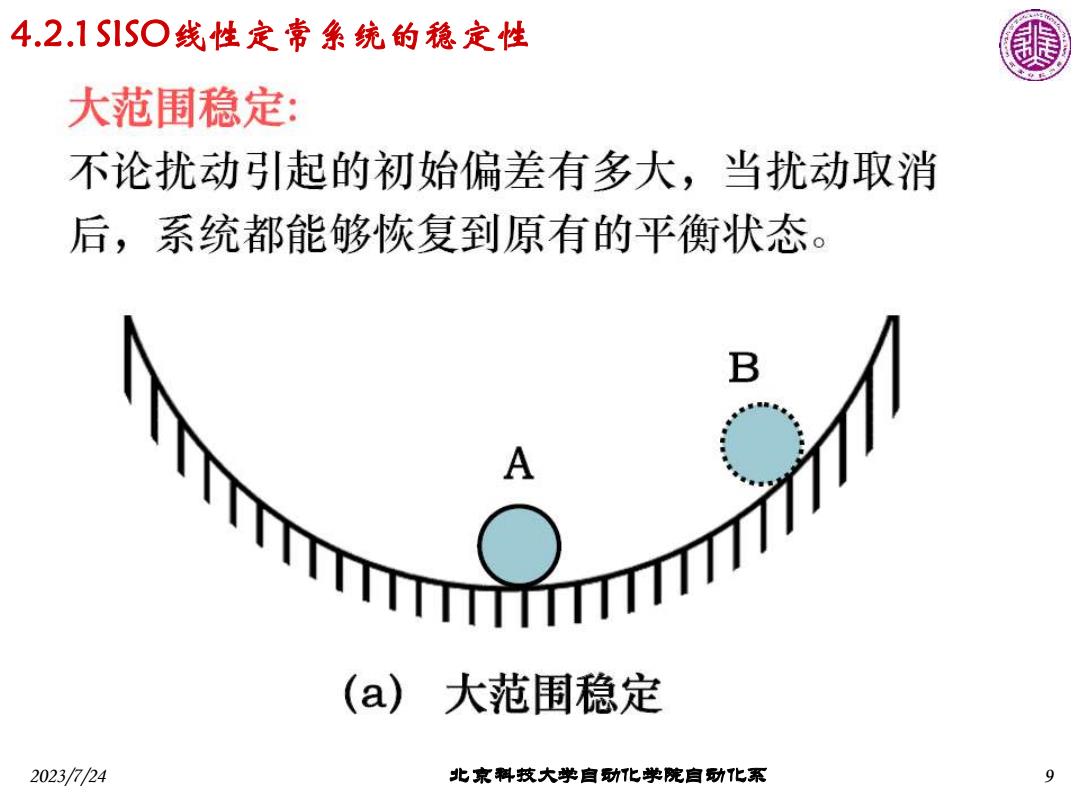
4.2.1S1S○线性定常象统的稳定性 大范围稳定: 不论扰动引起的初始偏差有多大,当扰动取消 后,系统都能够恢复到原有的平衡状态。 B A (a)大范围稳定 2023/724 北京料技大学自动化学院自功化系 9
2023/7/24 北京科技大学自动化学院自动化系 9 4.2.1 SISO线性定常系统的稳定性
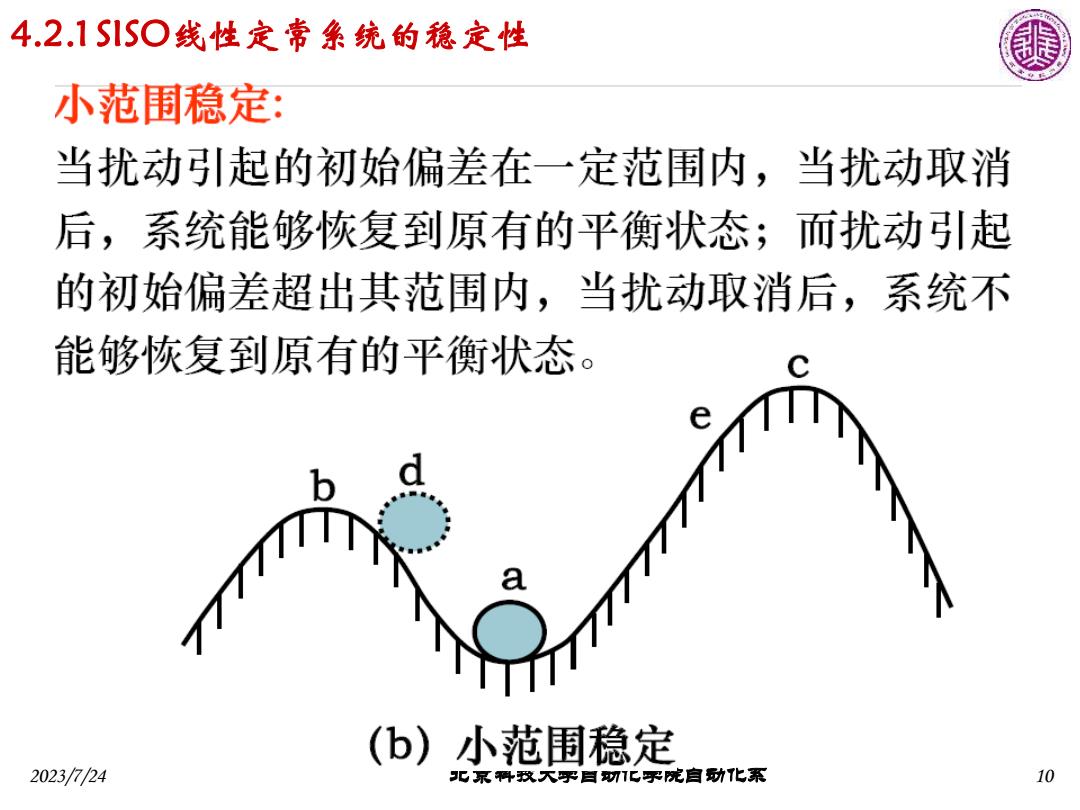
4.2.1S1S○线性定常象统的稳定性 小范围稳定: 当扰动引起的初始偏差在一定范围内,当扰动取消 后,系统能够恢复到原有的平衡状态;而扰动引起 的初始偏差超出其范围内,当扰动取消后,系统不 能够恢复到原有的平衡状态。 (b)小范围稳定 2023/724 北京科我天乎目1C子院自功化系 10
2023/7/24 北京科技大学自动化学院自动化系 10 4.2.1 SISO线性定常系统的稳定性