本章的引子 设计控制条统应完成哪些工作? 控制对象运动规律的描述 本章任 控制对象 控制对象运动规律定量分析 和 控制对象运动规律定性分析 控制系统 的 数学模型 控制系统的设计与综合 本章的数学基础一拉氏变换 2023/724 北京科较大学自动化学院控制系
2023/7/24 北京科技大学自动化学院控制系 1 设计控制系统应完成哪些工作? 控制对象运动规律的描述 控制对象运动规律定性分析 控制对象运动规律定量分析 控制系统的设计与综合 控制对象 和 控制系统 的 数学模型 本章任务 本章的引子 本章的数学基础——拉氏变换

2、控制系统的数学模型 2.1控制条统的运动方程 2.2线性条统的频城模型 2.3方框图与信号流图 小结 2023/724 北京料技大学自功化学院控制系 2
2023/7/24 北京科技大学自动化学院控制系 2 2、控制系统的数学模型 2.1 控制系统的运动方程 2.2 线性系统的频域模型 2.3 方框图与信号流图 小 结

本章学习要点 一简单物理条统的微分方程的列写; 一非线性模型的线性化方法; 一传递函数和传递函数矩阵的概念; 一结构图和信号流图的变换与化简; ⑤返回 2023/724 北京料技大学自功化学院控制系 3
2023/7/24 北京科技大学自动化学院控制系 3 本章学习要点 –简单物理系统的微分方程的列写; –非线性模型的线性化方法; –传递函数和传递函数矩阵的概念; –结构图和信号流图的变换与化简;
2.1控制系统的运功方程 例2.1.1 研究RLC电路,试找出输出电压u(t)随输入 电压u(t)变化的规律。 R 解 u,(t)=L i(+Ri(t))+u.() dt it) u(t) u.(t) (t)=C du,(t) dt Lcw.@+Rc,@+a.(④=u,(0 dt2 dt 。O○ R、C、L以及初 始uc(O)确定时,已 知u,(t)就可以确 定u(t) 2023/7/24 北京料技大学自动化学院控制系 4
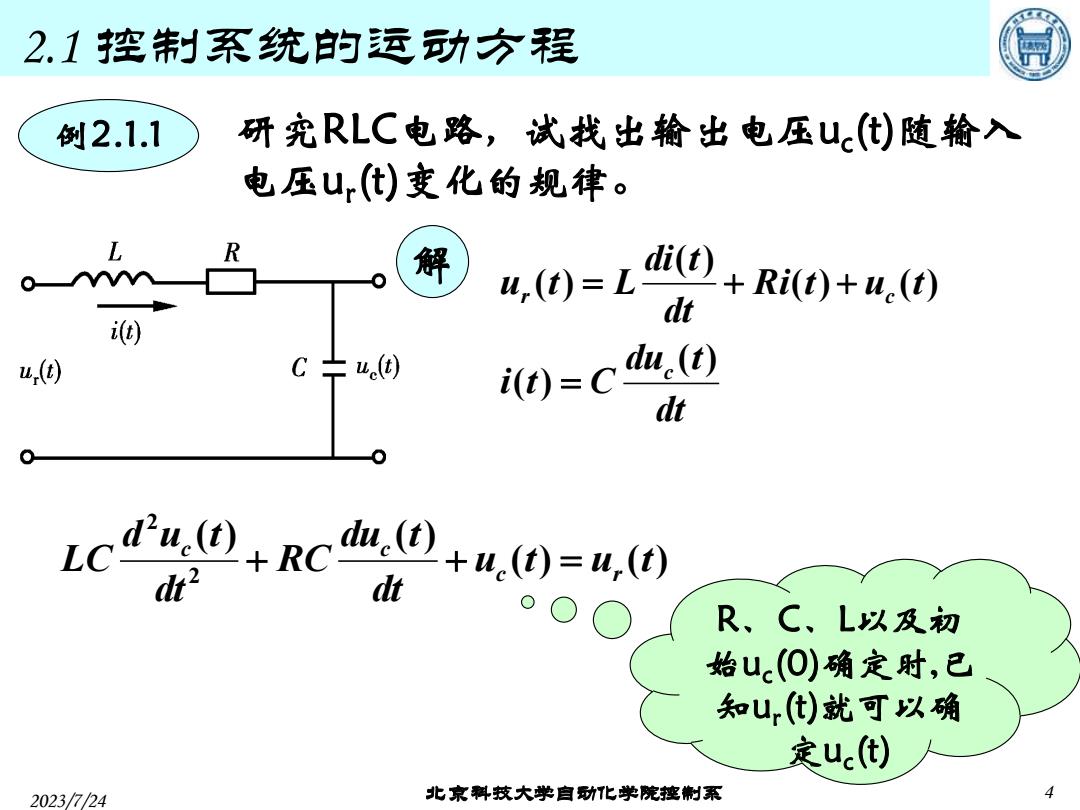
2023/7/24 北京科技大学自动化学院控制系 4 2.1 控制系统的运动方程 dt du t i t C Ri t u t dt di t u t L c r c ( ) ( ) ( ) ( ) ( ) ( ) = = + + 例2.1.1 研究RLC电路,试找出输出电压uc (t)随输入 电压ur (t)变化的规律。 解 R、C、L以及初 始uc (0)确定时,已 知ur (t)就可以确 定uc (t) ( ) ( ) ( ) ( ) 2 2 u t u t dt du t RC dt d u t LC c r c c + + =
2.1控制系统的运功方程 例2.1.2 如图:由质量为m的木块、弹性条数为K的 弹簧和阻尼系数为B的系统,试找出木块的 位移X(t)与外力F()之间的关系。 f) 解 d"x(t) f(t)-f(t)-fa(t)=m dr m f(t)=Kx(t) )=B dt m、K、B以及初 始X(O)确定时,已 9m一 0+B0+K)=f0 dr dt 知f(t)就可以确定 x(t) 2023/7/24 北京料技大学自功化学院控制系
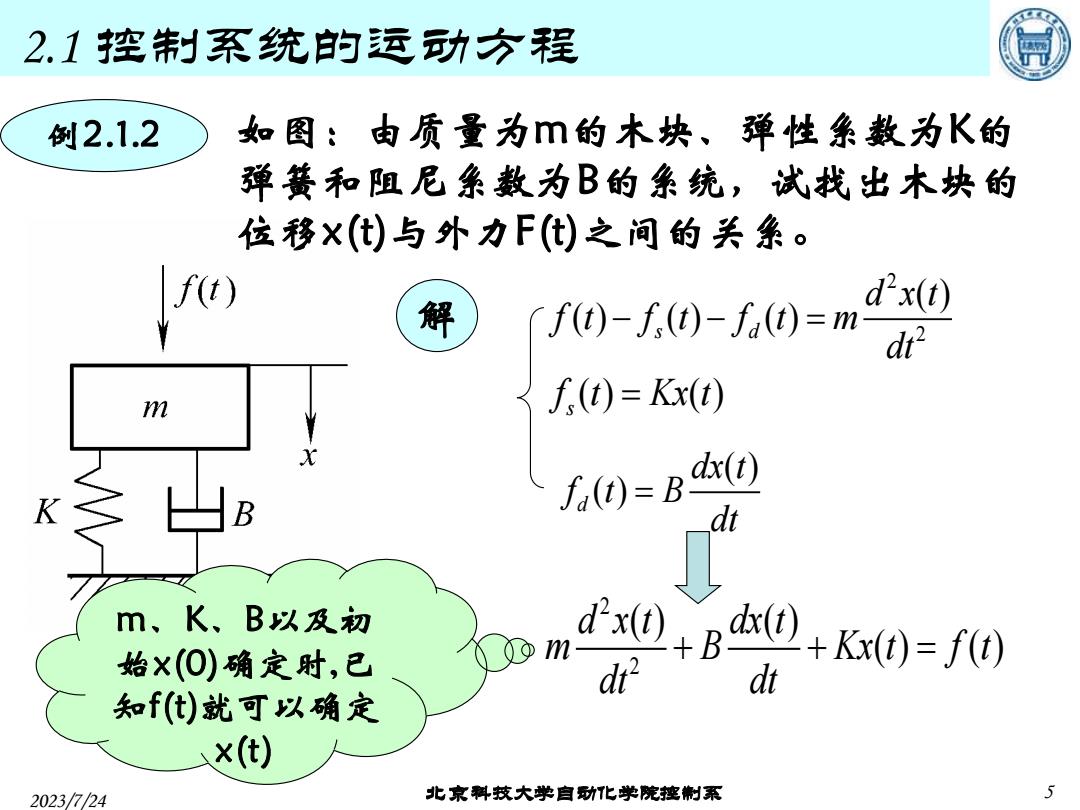
2023/7/24 北京科技大学自动化学院控制系 5 2.1 控制系统的运动方程 例2.1.2 如图:由质量为m的木块、弹性系数为K的 弹簧和阻尼系数为B的系统,试找出木块的 位移x(t)与外力F(t)之间的关系。 ( ) ( ) d dx t f t B dt = 2 2 ( ) ( ) ( ) ( ) d x t dx t m B Kx t f t dt dt + + = 2 2 ( ) ( ) ( ) ( ) s d d x t f t f t f t m dt − − = ( ) ( ) s f t Kx t = 解 m、K、B以及初 始x(0)确定时,已 知f(t)就可以确定 x(t)

2.1控制系统的运功方程 例2.1.3 直流他励电动机 电枢电路,取电枢电压 La Ra +0 ua为输入量,电动机角 速度①m为输出量,讨论 Ua 负载 JL 它们之间的关条。 解 电枢回路电压平衡方程:,0=L, di@+Ria①+E。 电动机轴上的转矩平衡方程: 电枢反电势 do.(D()M(-M( E,=C.o(t) dt J血:电动机和负载折合到电动机轴上的转动惯 电磁转矩方程:Mm=C,们通m电动机秘预整新腰猪絷数的 今L小.a0+亿.+RJ赛委表 dt2 山份是绳鼬赞较转矩 =Cm4()-L。 dM(t)_R,M.(t) dt 2023/7/24 北京料技大学自动化学院控制系 6
2023/7/24 北京科技大学自动化学院控制系 6 2.1 控制系统的运动方程 • 直流他励电动机 电枢电路,取电枢电压 ua为输入量,电动机角 速度ωm为输出量,讨论 它们之间的关系。 a a a a a a R i t E dt di t u t = L + ( )+ ( ) 电枢回路电压平衡方程: ( ) 电磁转矩方程: m m a M = C i (t) 电动机轴上的转矩平衡方程: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 R M t dt dM t C u t L R f C C t dt d t L f R J dt d t L J a c c m a a a m m e m m a m a m m a m = − − + + + + ( ) ( ) ( ) ( ) f t M t M t dt d t J m m m c m m + = − 例2.1.3 解 电枢反电势 E C (t) a = e 是电枢电流产生的电动转矩 是电动机转矩系数 M m m C M c (t)是折合到电动机轴上的总负载转矩 Jm:电动机和负载折合到电动机轴上的转动惯 量;fm:电动机和负载折合到电动机轴上的黏 性摩擦系数;

2.1控制系统的运功方程 注意观察三个示例的微分方程 一可以通过求解得到u()uc(),f(t)X)之间内在运 动的关联关条、分析系统的运动特性。 一进而改造系统-选择适当的R、L、C和m、B、K得 别香离的送熟规律。 许装击至看寐材华鬼无尖间乏处控利绕!1共 物稞背景能完全一样,可以用一个运动方程来 ”示,+线研可米车微地去研究其体亲统只好析 共款等香达式,即名们晶有湘同的数学搓型。,这类 L集统报春米a似绕。) +(Rafn+CCe)om(t) dt =Cmua(t))-La dM。①-RM.()-- --------例2.1.3 dt 2023/724 北京料技大学自功化学院控制系 7
2023/7/24 北京科技大学自动化学院控制系 7 2.1 控制系统的运动方程 • 注意观察三个示例的微分方程 – 可以通过求解得到ur (t)~uc (t),f(t)~x(t)之间内在运 动的关联关系、分析系统的运动特性。 – 进而改造系统-选择适当的R、L、C和m、B、K得 到希望的运动规律。 – 许多表面上看来似乎毫无共同之处的控制系统,其 物理背景可能完全一样, 可以用一个运动方程来 表示,我们可以不单独地去研究具体系统而只分析 其数学表达式,即它们具有相同的数学模型。这类 系统被称为相似系统。 2.1.3 2.1.2 2.1.1 例 例 例 = − − − − − − − − − − − − − − + + + + + + = − − − − − − − − − − − − + + = − − − − − − − − − ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 2 R M t dt dM t C u t L R f C C t dt d t L f R J dt d t L J K x t f t dt dx t B dt d x t m u t u t dt du t RC dt d u t LC a c c m a a a m m e m m a m a m m a m c r c c

2.1控制系统的运功方程 控制系统的运动一对系统施加控制(即输入控制信号), 从而得到系统输出量(即受控量)随时问的变化规律 (即输出响应信号)。 控制系统的运动方程一根据描述系统特性的物理学定律, 如机械,电气,热力,液压等方面的基本定律写出。 展示系统在运动过程中各变量之间的相互关条,既定 性又定量地描述整个系统的运动过程。 数学摸型一描述系统内部物理量(或变量)之间的数学 表达式,是分析和设计自动控制条统的基础。 静态模型:在静态条件下(即变量不随时间变化),描述变 量之间关条的代数方程(组)。 动态模型:描述变量各阶导数之间关系的微分方程(组)。 2023/724 北京料技大学自功化学院控制系 8
2023/7/24 北京科技大学自动化学院控制系 8 2.1 控制系统的运动方程 控制系统的运动—对系统施加控制(即输入控制信号), 从而得到系统输出量(即受控量)随时间的变化规律 (即输出响应信号)。 控制系统的运动方程—根据描述系统特性的物理学定律, 如机械,电气,热力,液压等方面的基本定律写出。 展示系统在运动过程中各变量之间的相互关系,既定 性又定量地描述整个系统的运动过程。 数学模型—描述系统内部物理量(或变量)之间的数学 表达式,是分析和设计自动控制系统的基础。 静态模型:在静态条件下(即变量不随时间变化),描述变 量之间关系的代数方程(组)。 动态模型:描述变量各阶导数之间关系的微分方程(组)

2.1控制系统的运功今程 建立数学模型的方法 >解析法一依据描述系统运动规律的运动定律来得 到微分方程的方法。 >实脸法一基于系统输入输出的实验数据来建立数 学模型的方法。 数学模型的形式 >附城模型一微分方程、差分方程和状态方程; >复频城模型一传递函数、结构图、频率特性。 20231724 北京料技大学自功化学院控制系 9
2023/7/24 北京科技大学自动化学院控制系 9 2.1 控制系统的运动方程 建立数学模型的方法 ➢解析法 —依据描述系统运动规律的运动定律来得 到微分方程的方法。 ➢实验法 —基于系统输入输出的实验数据来建立数 学模型的方法。 数学模型的形式 ➢时域模型—微分方程、差分方程和状态方程; ➢复频域模型—传递函数、结构图、频率特性

2.1控制系统的运功方程 问题:从严格意义上讲,绝大多数系统的数学模型都 不是线性模型(即条统并非是线性条统)。事实上, 任何一个元件总是存在一定程度的非线性。即使假设 具有线性的特性,也是局限在一定的范围内。 输出 输出 4输出 b 种常见的非线性 0 0 输入 0 输入 输入 a 饱和'(放大器) 死区(电机) 间隙(齿轮) 2023/724 北京料技大学自功化学院控制系 10
2023/7/24 北京科技大学自动化学院控制系 10 2.1 控制系统的运动方程 • 问题:从严格意义上讲,绝大多数系统的数学模型都 不是线性模型(即系统并非是线性系统)。事实上, 任何一个元件总是存在一定程度的非线性。即使假设 具有线性的特性,也是局限在一定的范围内。 几 种 常 见 的 非 线 性