
非线性自动控制系统 的分析与设计 付冬梅教授 fdm2003@163.com 北京科技大学自动化学院
非线性自动控制系统 的分析与设计 付冬梅 教授 fdm2003@163.com 北京科技大学自动化学院

主要内容 ·一、非线性系统的特征与定义 ·二、非线性对条统性能的影响 ·三、非线性条统的分析方法
主要内容 • 一、 非线性系统的特征与定义 • 二、 非线性对系统性能的影响 • 三、 非线性系统的分析方法

1.非线性系统概述 实际系统中,非线性的例子有很多,例如齿轮 间隙缝、电路中电和现象等。 一、非线性系统的特征与定义: 1.非线性系统输出相应曲线的形状与输入信号的大 小和象统的初始状态有关。 2.非线性系统的稳定性也与输入信号的大小和系 统的初始状态有关。 3.非线性系统常产生自激振荡。 4.非线性系统有畸变现象。 5.非线性系统可能会产生跳跃谐振。 6.非线性系统不适合叠加原理
1. 非线性系统概述 实际系统中,非线性的例子有很多,例如齿轮 间隙缝、电路中电和现象等。 一、非线性系统的特征与定义: 1. 非线性系统输出相应曲线的形状与输入信号的大 小和系统的初始状态有关。 2. 非线性系统的稳定性也与输入信号的大小和系 统的初始状态有关。 3. 非线性系统常产生自激振荡。 4. 非线性系统有畸变现象。 5. 非线性系统可能会产生跳跃谐振。 6. 非线性系统不适合叠加原理
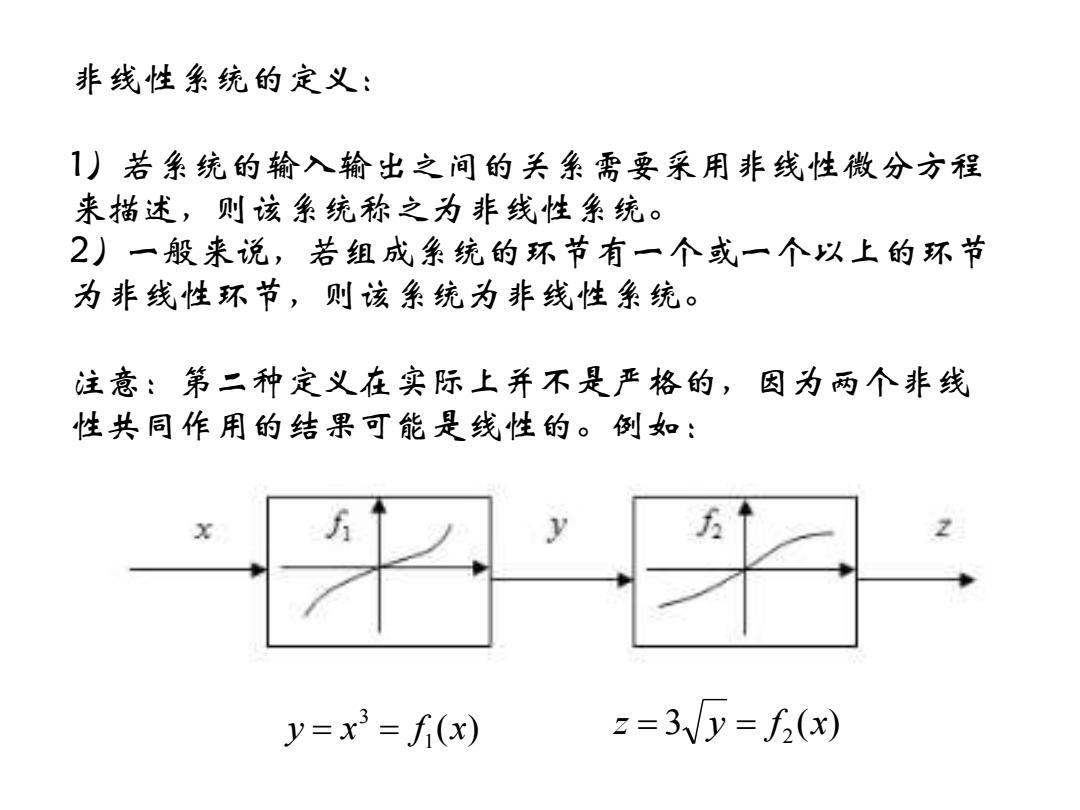
非线性系统的定义: 1)若系统的输入输出之间的关系需要采用非线性微分方程 来描述,则该系统称之为非线性系统。 2)一般来说,若组成系统的环节有一个或一个以上的环节 为非线性环节,则该系统为非线性系统。 注意:第二种定义在实际上并不是严格的,因为两个非线 性共同作用的结果可能是线性的。例如: y=x=f(x) z=3/y=f(x)
非线性系统的定义: 1)若系统的输入输出之间的关系需要采用非线性微分方程 来描述,则该系统称之为非线性系统。 2)一般来说,若组成系统的环节有一个或一个以上的环节 为非线性环节,则该系统为非线性系统。 注意:第二种定义在实际上并不是严格的,因为两个非线 性共同作用的结果可能是线性的。例如: ( ) 1 3 y = x = f x 3 ( ) 2 z = y = f x
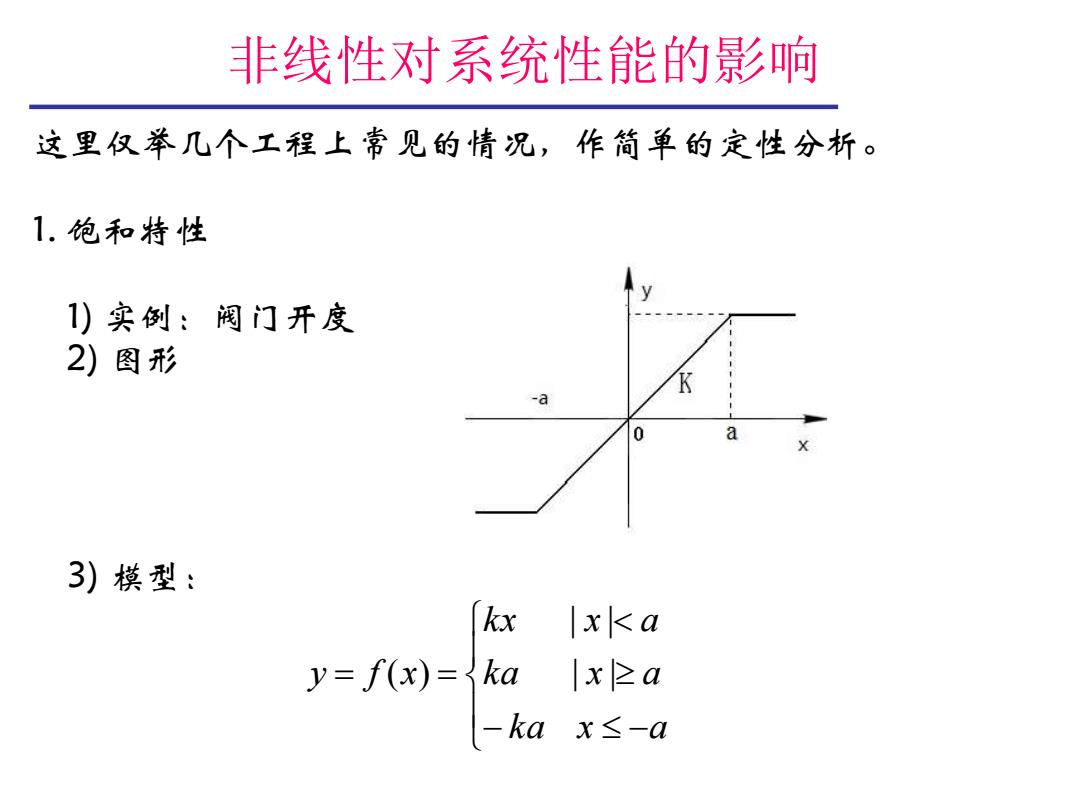
非线性对系统性能的影响 这里仅举几个工程上常见的情况,作简单的定性分析。 1.饱和特性 1)实例:阀门开度 2)图形 3)模型: kxx<a y=f(x)=ka xza -kax≤-a
非线性对系统性能的影响 这里仅举几个工程上常见的情况,作简单的定性分析。 1. 饱和特性 1) 实例:阀门开度 2) 图形 3) 模型: − − = = k a x a k a x a k x x a y f x | | | | ( )
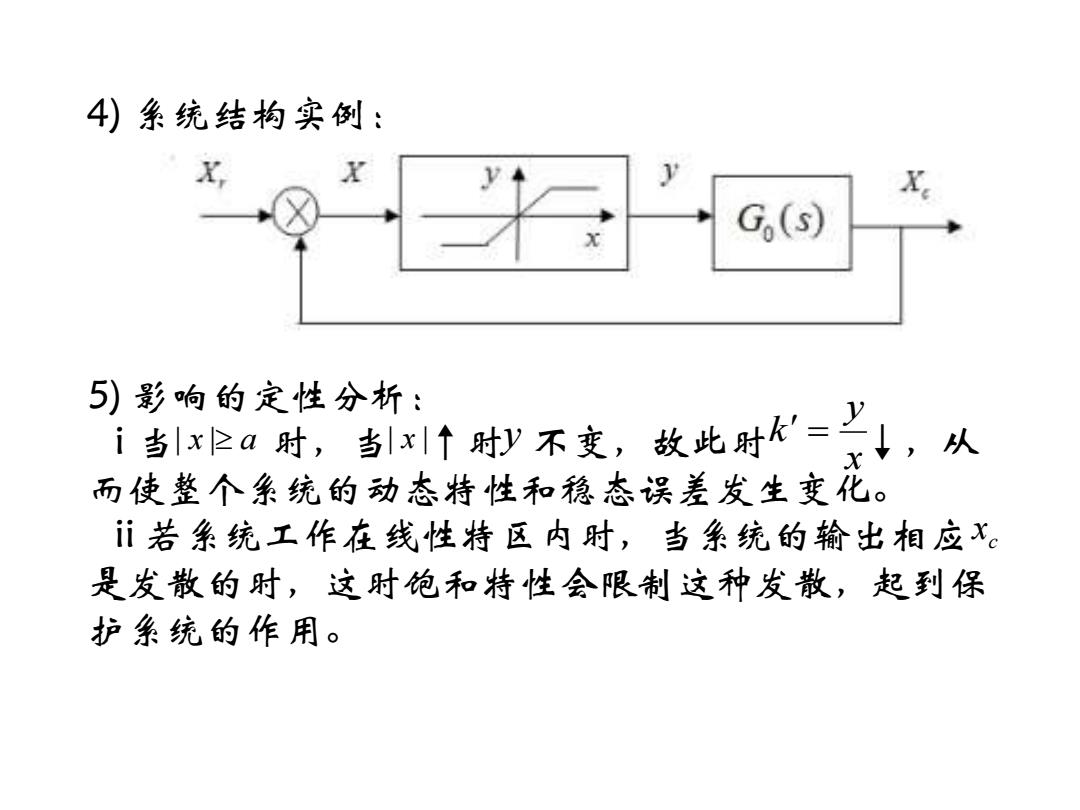
4)系统结构实例: X X X G,(s) 5)影响的定性分析: 当1&时,当个时y不变,故此附k=,从 X 而使整个系统的动态特性和稳态误差发生变化。 ⅱ若系统工作在线性特区内时,当系统的输出相应。 是发散的时,这时饱和特性会限制这种发散,起到保 护系统的作用
4) 系统结构实例: 5) 影响的定性分析: i 当 时,当 ↑时 不变,故此时 ↓,从 而使整个系统的动态特性和稳态误差发生变化。 ii 若系统工作在线性特区内时,当系统的输出相应 是发散的时,这时饱和特性会限制这种发散,起到保 护系统的作用。 | x | a | x | y x y k = c x

2.死区特性 )实例:齿轮的缝隙的影响 2)图形: y X 3)模型: k(x-asign(x))x=a y=f)= x<a
2. 死区特性 1) 实例:齿轮的缝隙的影响 2) 图形: 3) 模型: − = = x a k x asign x x a y f x 0 | | ( ( )) | | ( )

4)系统结构实例: X X G(s) G,(S) 5)影响的定性分析:(考虑特殊的的情况) 使巳增加,即这种情况下,一般巳s不可能为零。 可以滤掉小幅值的干扰。 图为此条统的非线性部分,当X↑时,《三↑,所以彩 统的动态信号特性与X的大小有关。 当输入是f、之w叶等附变信号,无区的存在会产坐 因为只有当输入信号大于☑或小于一时才会有输出相应
4) 系统结构实例: 5) 影响的定性分析:(考虑特殊的的情况) 使 增加,即这种情况下,一般 不可能为零。 可以滤掉小幅值的干扰。 因为此系统的非线性部分,当 ↑时, ↑,所以系 统的动态信号特性与 的大小有关。 当输入是 、 、 等时变信号,死区的存在会产生, 因为只有当输入信号大于 或小于 时才会有输出相应。 ss e ss e x x y k = x t 2 2 1 t sin wt a −a
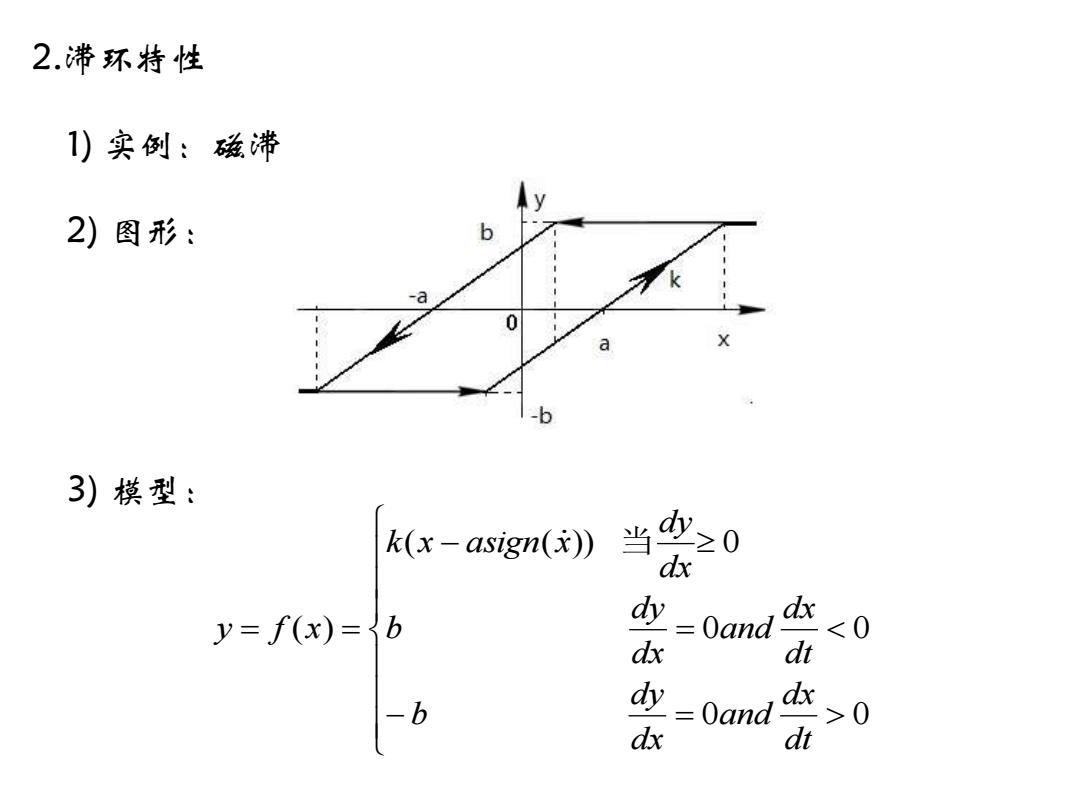
2.滞环特性 1)实例:磁滞 2)图形: b 3)模型: k(x-asign(》当 y dx dx y=f(x)=3b y-Oand ∠0 -B .=Oand dx 70
2.滞环特性 1) 实例:磁滞 2) 图形: 3) 模型: − = = − = = 0 0 0 0 ( ( )) 0 ( ) dt dx and dx dy b dt dx and dx dy b dx dy k x asign x y f x 当
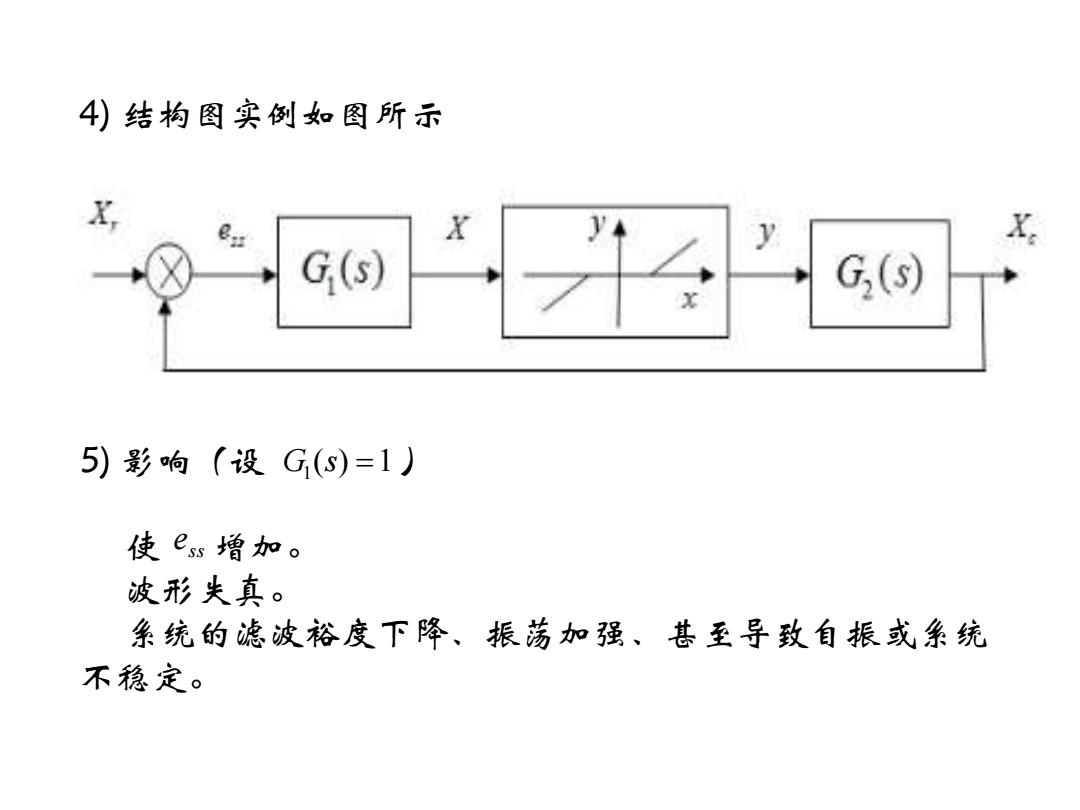
4)结构图实例如图所示 X X X G(s) G() 5)影响(设G(S)=1) 使巳s增加。 波形失真。 系统的滤波裕度下降、振荡加强、甚至导致自振或系统 不稳定
4) 结构图实例如图所示 5) 影响(设 ) 使 增加。 波形失真。 系统的滤波裕度下降、振荡加强、甚至导致自振或系统 不稳定。 G1 (s) =1 ss e