
一级学科课程 土木工程(0814) 课程编号 课程名称 课程大纲撰写人 S081400X0001 矩阵论 402戴天时 S081400XI002 非线性泛函分析 402 吉敏 S081400X003 概率论与数理统计 402 S081400X004 数值分析 402 曹礼群 S081400XJ005 数学物理方程 402 华士鸣 s081400XI006 随机讨程 402 张三国 S081400X007 有限元方法 402 田完 S081400XJ008 弹塑性力学 402 戴兰宏 科S081400X0009 材料力学 402董心 其0g1400X1010 计算机图形学理论与应用 402 汁吉(像改) S081400X1011 工程地质学 402 伍法权,徐嘉漠 S081400XJ012 地球动力学 402 石耀霖 S081400XJ013 地球介质力学 402 魏东平 合 学科专家组签字: 学院(系)盖章
一级学科课程 土木工程(0814) 属 性 课程编号 课程名称 学 时 学 分 课程大纲撰写人 学 科 基 础 课 S081400XJ001 矩阵论 40 2 戴天时 S081400XJ002 非线性泛函分析 40 2 吉敏 S081400XJ003 概率论与数理统计 40 2 修改 S081400XJ004 数值分析 40 2 曹礼群 S081400XJ005 数学物理方程 40 2 华士鸣 S081400XJ006 随机过程 40 2 张三国 S081400XJ007 有限元方法 40 2 田宗漱 S081400XJ008 弹塑性力学 40 2 戴兰宏 S081400XJ009 材料力学 40 2 董心 S081400XJ010 计算机图形学理论与应用 40 2 沈青(修改) S081400XJ011 工程地质学 40 2 伍法权,徐嘉谟 S081400XJ012 地球动力学 40 2 石耀霖 S081400XJ013 地球介质力学 40 2 魏东平 学 科 综 合 课 学院(系)盖章 学科专家组签字:
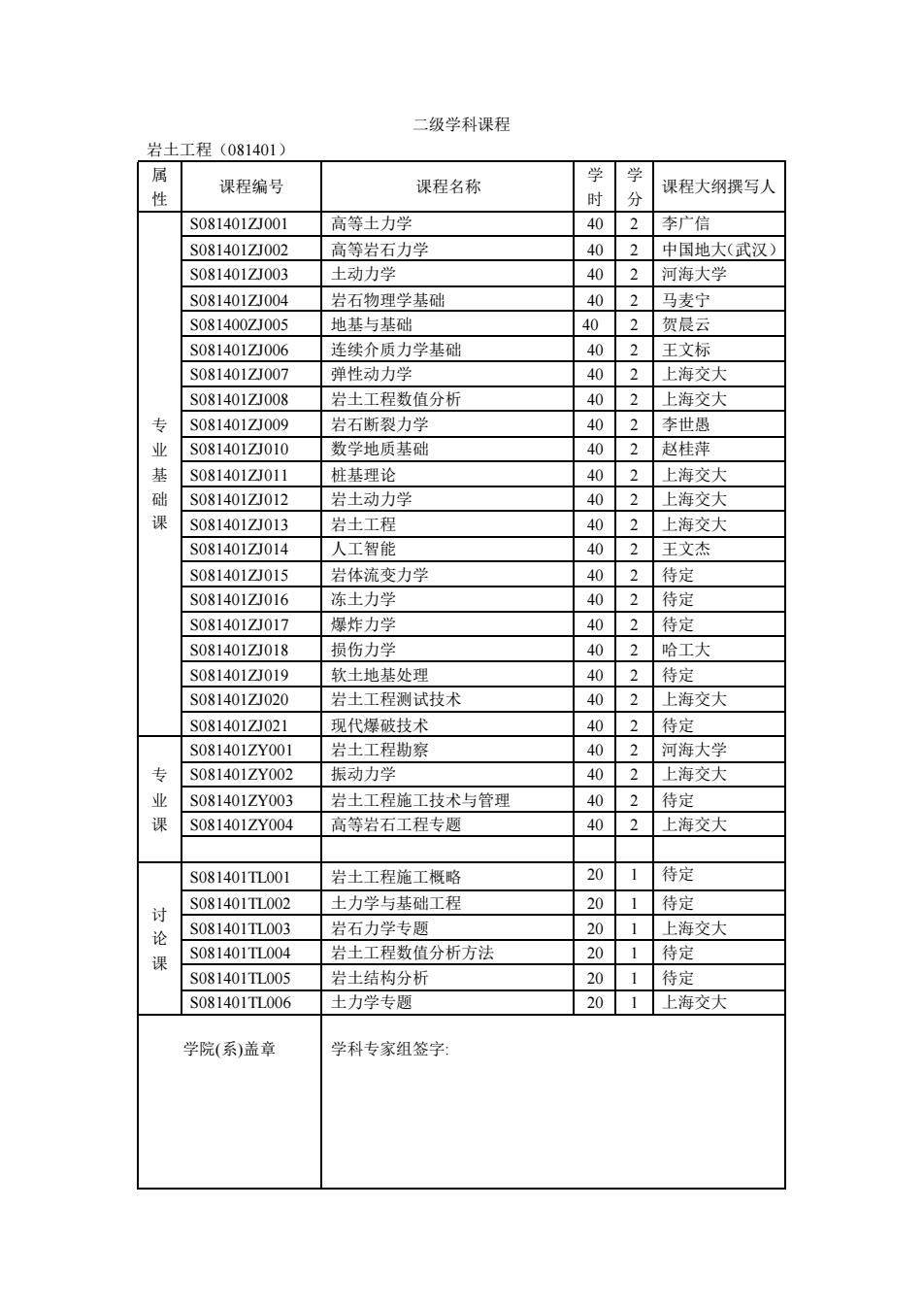
二级学科课程 岩土工程(081401) 课程编号 课程名称 学 学 课程大纲撰写人 S0814017I001 高第十力学 402李广信 S081401Z002 高等岩石力学 402中国地大(武汉) S081401ZJ003 土动力学 402河海大学 S081401ZJ004 岩石物理学基础 402马麦宁 S081400ZJ005 地其上与其 402贺晨云 S081401ZJ006 连缕介质力学基础 402王文标 S081401Z☒007 弹性动力学 402 上海交大 S0814017J008 岩土工程数值分析 402上海交大 S081401ZJ009 岩石断裂力学 402李世愚 S081401ZJ010 数学地质基础 402赵桂萍 S081401ZJ011 桩基理论 402 上海交大 S081401ZJ012 岩土动力学 402上海交大 课S081401Z013 岩土工程 402.上海交大 S081401ZJ014 人工智能 402王文杰 S081401ZJ015 岩体流变力学 402 待定 S081401ZJ016 冻土力学 402待定 081401ZJ017 绿桥力学 402待定 Ss081401ZJ018 损伤力学 0 2哈工大 S081401ZJ019 软土地基处理 402 特定 S081401ZJ020 岩土工程测试技术 402上海交大 S08140171021 现代爆破持术 402待定 S081401ZY001 岩土工程勘察 402河海大学 S081401ZY002 振动力学 402上海交大 S081401Zy003 岩十T程施丁持术与持理 402待定 S081401ZY004 高等岩石工程专颗 402上海交大 s081401I001 岩土工程临工概略 201待定 081401Tm002 土力学与基础工程 201待定 S081401Tm003 岩石力学专圈 201上海交 S081401TL004 岩土工程数值分析方法 课 201待定 S081401T1005 岩十结构分析 201巷定 S081401TL006 土力学专题 201上海交大 学院(系)盖章 学科专家组签
二级学科课程 岩土工程(081401) 属 性 课程编号 课程名称 学 时 学 分 课程大纲撰写人 专 业 基 础 课 S081401ZJ001 高等土力学 40 2 李广信 S081401ZJ002 高等岩石力学 40 2 中国地大(武汉) S081401ZJ003 土动力学 40 2 河海大学 S081401ZJ004 岩石物理学基础 40 2 马麦宁 S081400ZJ005 地基与基础 40 2 贺晨云 S081401ZJ006 连续介质力学基础 40 2 王文标 S081401ZJ007 弹性动力学 40 2 上海交大 S081401ZJ008 岩土工程数值分析 40 2 上海交大 S081401ZJ009 岩石断裂力学 40 2 李世愚 S081401ZJ010 数学地质基础 40 2 赵桂萍 S081401ZJ011 桩基理论 40 2 上海交大 S081401ZJ012 岩土动力学 40 2 上海交大 S081401ZJ013 岩土工程 40 2 上海交大 S081401ZJ014 人工智能 40 2 王文杰 S081401ZJ015 岩体流变力学 40 2 待定 S081401ZJ016 冻土力学 40 2 待定 S081401ZJ017 爆炸力学 40 2 待定 S081401ZJ018 损伤力学 40 2 哈工大 S081401ZJ019 软土地基处理 40 2 待定 S081401ZJ020 岩土工程测试技术 40 2 上海交大 S081401ZJ021 现代爆破技术 40 2 待定 专 业 课 S081401ZY001 岩土工程勘察 40 2 河海大学 S081401ZY002 振动力学 40 2 上海交大 S081401ZY003 岩土工程施工技术与管理 40 2 待定 S081401ZY004 高等岩石工程专题 40 2 上海交大 讨 论 课 S081401TL001 岩土工程施工概略 20 1 待定 S081401TL002 土力学与基础工程 20 1 待定 S081401TL003 岩石力学专题 20 1 上海交大 S081401TL004 岩土工程数值分析方法 20 1 待定 S081401TL005 岩土结构分析 20 1 待定 S081401TL006 土力学专题 20 1 上海交大 学院(系)盖章 学科专家组签字:
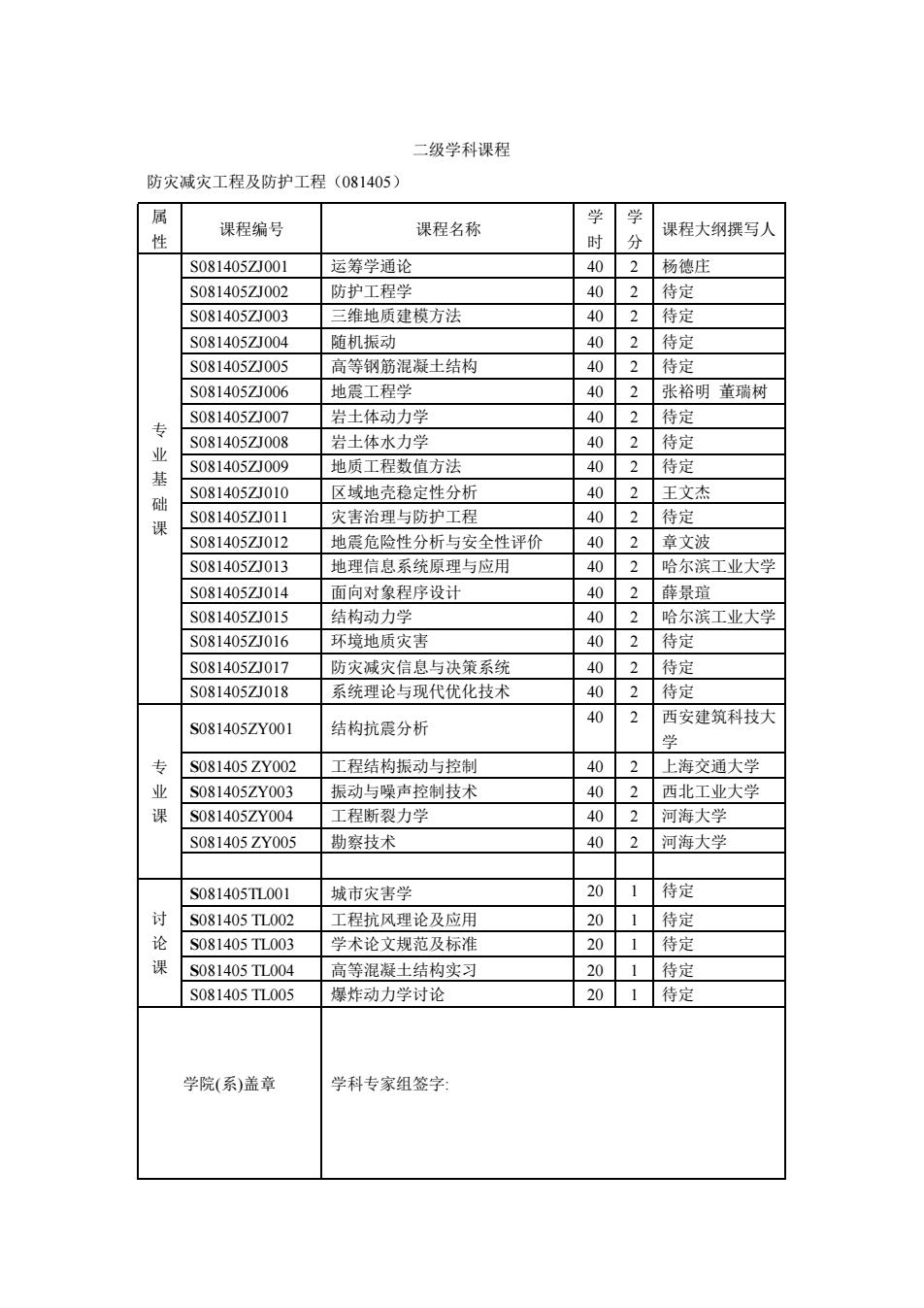
二级学科课程 防灾减灾工程及防护工程(081405) 课程编号 课程名称 学学 课程大纲撰写人 S081405ZJ001 运筹学通论 402杨德庄 g08140571002 防护T积学 402待定 S081405Z003 三维地质建模方法 402待定 S081405ZJ004 随机振动 402特定 S081405ZJ005 高等钢筋混凝土结构 402待定 S0R140571006 地需了架学 402张裕明董瑞树 S081405Z007 岩土体动力学 402待定 S0814057J008 岩土体水力学 402待定 S081405ZJ009 地质工程数值方法 402待定 c0R140571010 风域地壳稳定性分析 402王文本 S081405ZJ011 灾治理与防护工程 402待定 S081405ZJ012 地震危险性分析与安全性评价 402章文波 S081405ZJ013 地理信总系统原理与应用 402哈尔滨工业大学 c0R140571014 面向对象程序设计 402薛最瑞 S081405Z☑015 结构动力学 402哈尔滨工业大学 S0814057ZJ016 环境地质灾害 402待定 S0814057J017 防灾减灾信息与决策系统 402待定 S081405ZJ018 系统理论与现代优化技术 402特定 S081405ZY00 结构抗震分析 40 2 西安建筑科技大 专 S081405ZY002 工程结构振动与控制 402上海交通大学 c0e14057y003 振动与躁声控制技术 402西北工业大学 S081405ZY004 工程断裂力学 402河海大学 S081405ZY005 勘察技术 402河海大学 S081405TL001 城市灾害学 201待定 S081405TL002 工程抗风理论及应用 201待定 S081405TL003 学术论文规范及标准 201待定 课 S081405TI004 高等湿凝土结构实习 201待定 S081405T005 爆炸动力学讨论 201待定 学院(系)盖章 学科专家组签字
二级学科课程 防灾减灾工程及防护工程(081405) 属 性 课程编号 课程名称 学 时 学 分 课程大纲撰写人 专 业 基 础 课 S081405ZJ001 运筹学通论 40 2 杨德庄 S081405ZJ002 防护工程学 40 2 待定 S081405ZJ003 三维地质建模方法 40 2 待定 S081405ZJ004 随机振动 40 2 待定 S081405ZJ005 高等钢筋混凝土结构 40 2 待定 S081405ZJ006 地震工程学 40 2 张裕明 董瑞树 S081405ZJ007 岩土体动力学 40 2 待定 S081405ZJ008 岩土体水力学 40 2 待定 S081405ZJ009 地质工程数值方法 40 2 待定 S081405ZJ010 区域地壳稳定性分析 40 2 王文杰 S081405ZJ011 灾害治理与防护工程 40 2 待定 S081405ZJ012 地震危险性分析与安全性评价 40 2 章文波 S081405ZJ013 地理信息系统原理与应用 40 2 哈尔滨工业大学 S081405ZJ014 面向对象程序设计 40 2 薛景瑄 S081405ZJ015 结构动力学 40 2 哈尔滨工业大学 S081405ZJ016 环境地质灾害 40 2 待定 S081405ZJ017 防灾减灾信息与决策系统 40 2 待定 S081405ZJ018 系统理论与现代优化技术 40 2 待定 专 业 课 S081405ZY001 结构抗震分析 40 2 西安建筑科技大 学 S081405 ZY002 工程结构振动与控制 40 2 上海交通大学 S081405ZY003 振动与噪声控制技术 40 2 西北工业大学 S081405ZY004 工程断裂力学 40 2 河海大学 S081405 ZY005 勘察技术 40 2 河海大学 讨 论 课 S081405TL001 城市灾害学 20 1 待定 S081405 TL002 工程抗风理论及应用 20 1 待定 S081405 TL003 学术论文规范及标准 20 1 待定 S081405 TL004 高等混凝土结构实习 20 1 待定 S081405 TL005 爆炸动力学讨论 20 1 待定 学院(系)盖章 学科专家组签字:

大纲编号:S081400XJ001 矩阵论 Matrix Theory 课程编号:S081400XJ001课程属性:学科基础课 学时/学分:40/2 预修课程:高等数学、线性代数 教学目的和要求: 本课程为土木工程学科硕士研究生的学科基础课。通过本课程的学习,使学生进一步 握矩阵Jordan标准形、矩阵分解、矩阵微积分、矩阵函数以及线性空间与线性变换等方面 的基本概念、基本理论和基本方法,培养学生在有限维线性空间的框架下利用矩阵理论分析 和解决工程实际问题的能力,同时在抽象思维、罗辑推理、联想对比以及分析综合等方面提 高学生的数学素质。要求学生对课程内容有较系统的理解,掌握相关的基本概念、基本理论 和基本方法,并具有初步的应用能力。 内容提要: 第一章绪论 数域,一元多项式的基本概念,整除性,最大公因式,复数域上的标准分解,共轭矩阵, Hermite矩阵,Hermite一次型,西矩阵,矩阵的迹,矩阵的相似对角化与特征向量系的完 备性,矩阵的直积。 第二章矩阵的Jordan标准形 多项式矩阵的秩,方阵可逆性,初等变换下的标准形式,行列式因子,不变因子,初等 因子,两多项式矩阵等价的充要条件,两数字方阵相似的充要条件,矩阵的Jordan标准形, 矩阵与其Jordan形间相似变换矩阵的求法,矩阵的致零多项式与最小多项式。 第三章线性空间与线性变换 空间的定义,性质,基与维数,坐标,基变换与坐标变换,线性变换及其运算,线 性变换的矩阵,线性子空间,子空间的和与直和,不变子空间。 第四章内积空间 内积空间的定义,性质,标准正交基,Schmidt正交化方法,欧氏空间的度量矩阵,正 交子空间,正交变换与对称变换,酉空间。 第五章矩阵分解与广义 矩阵的正交三角分解,满秩分解,谱分解,正规矩阵及其分解,奇异值分解,矩阵的 MP广义逆。 第六章向量与矩阵的范数 向量范数定义,常用的几种向量范数,向量范数的等价性,矩阵范数的定义,乘法相容 性,与向量范数的相容性,由向量范数导出的矩阵范数,列和范数,行和范数,谱范数 F-范数,矩阵范数的等价性,矩阵的测度及其性质,范数应用举例 第七章矩阵分析 向量序列与矩阵序列的收敛性,函数矩阵对变量的导数,函数对矩阵的导数,矩阵对矩 阵的导数,矩阵的微分与积分,矩阵级数的收敛性,矩阵幂级数的收敛性。 第八章矩阵函数及其应用 用幂级数表示的矩阵函数,矩阵多项式的计算 一般矩阵函数的定义及性质,利用Jordar 形计算矩阵函数,利用Lagrange-Sylvester插值多项式计算矩阵函数,利用矩阵函数求解 阶常系数微分方程组的初值问题
大纲编号:S081400XJ001 矩阵论 Matrix Theory 课程编号: S081400XJ001 课程属性:学科基础课 学时/学分:40/2 预修课程:高等数学、线性代数 教学目的和要求: 本课程为土木工程学科硕士研究生的学科基础课。通过本课程的学习,使学生进一步掌 握矩阵 Jordan 标准形、矩阵分解、矩阵微积分、矩阵函数以及线性空间与线性变换等方面 的基本概念、基本理论和基本方法,培养学生在有限维线性空间的框架下利用矩阵理论分析 和解决工程实际问题的能力,同时在抽象思维、逻辑推理、联想对比以及分析综合等方面提 高学生的数学素质。要求学生对课程内容有较系统的理解,掌握相关的基本概念、基本理论 和基本方法,并具有初步的应用能力。 内容提要: 第一章 绪论 数域,一元多项式的基本概念,整除性,最大公因式,复数域上的标准分解,共轭矩阵, Hermite 矩阵,Hermite 二次型,酉矩阵,矩阵的迹,矩阵的相似对角化与特征向量系的完 备性,矩阵的直积。 第二章 矩阵的 Jordan 标准形 多项式矩阵的秩,方阵可逆性,初等变换下的标准形式,行列式因子,不变因子,初等 因子,两多项式矩阵等价的充要条件,两数字方阵相似的充要条件,矩阵的 Jordan 标准形, 矩阵与其 Jordan 形间相似变换矩阵的求法,矩阵的致零多项式与最小多项式。 第三章 线性空间与线性变换 线性空间的定义,性质,基与维数,坐标,基变换与坐标变换,线性变换及其运算,线 性变换的矩阵,线性子空间,子空间的和与直和,不变子空间。 第四章 内积空间 内积空间的定义,性质,标准正交基,Schmidt 正交化方法,欧氏空间的度量矩阵,正 交子空间,正交变换与对称变换,酉空间。 第五章 矩阵分解与广义逆 矩阵的正交三角分解,满秩分解,谱分解,正规矩阵及其分解,奇异值分解,矩阵的 M-P 广义逆。 第六章 向量与矩阵的范数 向量范数定义,常用的几种向量范数,向量范数的等价性,矩阵范数的定义,乘法相容 性,与向量范数的相容性,由向量范数导出的矩阵范数,列和范数,行和范数,谱范数, F-范数,矩阵范数的等价性,矩阵的测度及其性质,范数应用举例。 第七章 矩阵分析 向量序列与矩阵序列的收敛性,函数矩阵对变量的导数,函数对矩阵的导数,矩阵对矩 阵的导数,矩阵的微分与积分,矩阵级数的收敛性,矩阵幂级数的收敛性。 第八章 矩阵函数及其应用 用幂级数表示的矩阵函数,矩阵多项式的计算,一般矩阵函数的定义及性质,利用 Jordan 形计算矩阵函数,利用 Lagrange-Sylvester 插值多项式计算矩阵函数,利用矩阵函数求解一 阶常系数微分方程组的初值问题

主要参考书: 1。越天时主编。【矩隆论》(第一版),吉林到学技术中版补,长春,002。 2。李正良等编,《矩阵理论及其应用》。电子科技大学出版社,成都,19%6。 3.程云鹏主编,《矩阵论》(第二版),西北工业大学出版社,西安,1999。 捷写人:戴天时(中国科学院长春光学精密机械与物理研究所) 揍写日期:2002年11日
主要参考书: 1.戴天时主编,《矩阵论》(第二版),吉林科学技术出版社,长春,2002。 2.李正良等编,《矩阵理论及其应用》,电子科技大学出版社,成都,1996。 3.程云鹏主编,《矩阵论》(第二版),西北工业大学出版社,西安,1999。 撰写人: 戴天时(中国科学院长春光学精密机械与物理研究所) 撰写日期: 2002 年 11 日

大纲编号:S081400XJ002 非线性泛函分析 Nonlinear Functional Analysis 课程编号:S081400XJ002课程属性:学科基础课 学时/学分:40/2 预修课程:微积分、点集拓扑、线性泛函分析 教学目的和要求: 本课程为数学 土木工程各专业博士、硕士研究生的学科基础课,也可作为自然科学其 它专业的选修课。数学内部以及自然科学提出许多非线性问题,本课程正是介绍求解非线性 方程的一些方法,包括扑拓度理论,单调算子理论以及变分方法。在这个课程中,可以获得 非线性分析最基本的思想、概念、方法,为今后独立解决各种非线性问题打下基础。 内容提要: 第一章有穷维空间的拓扑度 度的构造及基本性质:Brouwer不动点定理:Hedgehog定理:Jordan分离定理:无界 集上的拓扑度。 第二章无穷维空间的拓扑度 关于Banach空间的基本知识:紧映射:Leray-Shauder度:Shauder不动点定理:可微 映射的度。 第三章单调映射及Accretive映射 单调映射的基本性质:Poincare算子:满映射定理:极大单调映射:半内积:Accretive 映射 第四章变分理论 变分方法:泛函的极值理论:Nehari技巧:伪梯度流:形变定理:极小极大原理: 数Lasterir-SchnirelAmann定理:指标理论:Morc不等式。 敕材: Klaus Deimling,Nonlinear Functional Analysis,Springer-Verlag.Berlin,Heidelberg,New York-Tokyo 1985 主要参考书: 1.陈文原,《非线性泛函分析》,甘肃人民出版社。 2.张恭庆,《临界点理论及应用》,科学出版社,北京,1986。 舞写人:吉敏(数学与系统科学研究院) 撰写日期:2001年11日
大纲编号:S081400XJ002 非线性泛函分析 Nonlinear Functional Analysis 课程编号: S081400XJ002 课程属性:学科基础课 学时/学分:40/2 预修课程:微积分、点集拓扑、线性泛函分析 教学目的和要求: 本课程为数学、土木工程各专业博士、硕士研究生的学科基础课,也可作为自然科学其 它专业的选修课。数学内部以及自然科学提出许多非线性问题,本课程正是介绍求解非线性 方程的一些方法,包括扑拓度理论,单调算子理论以及变分方法。在这个课程中,可以获得 非线性分析最基本的思想、概念、方法,为今后独立解决各种非线性问题打下基础。 内容提要: 第一章 有穷维空间的拓扑度 度的构造及基本性质;Brouwer 不动点定理;Hedgehog 定理;Jordan 分离定理;无界 集上的拓扑度。 第二章 无穷维空间的拓扑度 关于 Banach 空间的基本知识;紧映射;Leray-Shauder 度;Shauder 不动点定理;可微 映射的度。 第三章 单调映射及 Accretive 映射 单调映射的基本性质;Poincare 算子;满映射定理;极大单调映射;半内积;Accretive 映射。 第四章 变分理论 变分方法;泛函的极值理论;Nehari 技巧;伪梯度流;形变定理;极小极大原理;畴 数 Lüsternir-SchnirelAmann 定理;指标理论;Morse 不等式。 教材: Klaus Deimling,Nonlinear Functional Analysis,Springer-Verlag, Berlin,Heidelberg,New York-Tokyo, 1985. 主要参考书: 1. 陈文原,《非线性泛函分析》,甘肃人民出版社。 2. 张恭庆,《临界点理论及应用》,科学出版社,北京,1986。 撰写人: 吉敏(数学与系统科学研究院) 撰写日期: 2001 年 11 日

大纲编号:S081400XJ003 概率论与数理统计 Probability Theory and Mathematical Statistics 课程编号:S081400XJ003 课程属性:学科基础课 学时/学分:40/2 预悠课程:微积分、线性代数 教学目的和要求: 通过本课程的学习,应使学生掌握概率论与数理统计的基本概念,了解它的基本理论和 方法,从而使学生初步攀握处理随机现象的基本思想和方法,培养学生运用概率统计方法分 析和解决实际问题的能力。 内容提要: 第一章随机事件及其概率 重点掌提概率、条件概率、三大公式及事件独立性的概念 第二章随机变量及其分布 重点理解随机变量、密度、分布函数的概念,掌据正态分布及随机变量的相互独 立性 第三章随机变量的数字特征 重点堂据数学期望、方第的概念与计算,了解协方差与相关系数的概今 第四章特征函数 掌握特征函数的定义、性质与计算,了解特征函数与分布函数之间的关系。 第五章大数定理与中心极限定理 掌握大数定理与中心极限定理的定义及内容,熟悉三种收敛之间的关系。 第六章样本分析 重点掌握样本分布中的基本概念,熟悉样本分布定理。 第七章统计估计 重点理解点估计、区间估计的概念。 第八章假设检验 重点理解假设检验的基本思想:掌握假设检验的基本步骤。 教材: 1.《概率论与数理统计》,周誓达主编,人民大学出版社,2004年 主要参考书: 1。普通高等教有“十五”国家级规划教材(高职高专教有)《概率论与数理统计》(第 二版)金炳陶编著等教有出版社2000年8月第1版2004年5月第2版2004年8月第2次 印刷 撰写人: 摆写日期:
大纲编号:S081400XJ003 概率论与数理统计 Probability Theory and Mathematical Statistics 课程编号: S081400XJ003 课程属性:学科基础课 学时/学分:40/2 预修课程:微积分、线性代数 教学目的和要求: 通过本课程的学习,应使学生掌握概率论与数理统计的基本概念,了解它的基本理论和 方法,从而使学生初步掌握处理随机现象的基本思想和方法,培养学生运用概率统计方法分 析和解决实际问题的能力。 内容提要: 第一章 随机事件及其概率 重点掌握概率、条件概率、三大公式及事件独立性的概念 第二章 随机变量及其分布 重点理解随机变量、密度、分布函数的概念,掌握正态分布及随机变量的相互独 立性 第三章 随机变量的数字特征 重点掌握数学期望、方差的概念与计算,了解协方差与相关系数的概念 第四章 特征函数 掌握特征函数的定义、性质与计算,了解特征函数与分布函数之间的关系。 第五章 大数定理与中心极限定理 掌握大数定理与中心极限定理的定义及内容,熟悉三种收敛之间的关系。 第六章 样本分析 重点掌握样本分布中的基本概念,熟悉样本分布定理。 第七章 统计估计 重点理解点估计、区间估计的概念。 第八章 假设检验 重点理解假设检验的基本思想;掌握假设检验的基本步骤。 第九章 方差分析与回归分析 重点掌握方差分析与回归分析的方法 教材: 1.《概率论与数理统计》,周誓达 主编,人民大学出版社, 2004 年 主要参考书: 1. 普通高等教育“十五”国家级规划教材(高职高专教育)《概率论与数理统计》(第 二版)金炳陶编著等教育出版社 2000 年 8 月第 1 版 2004 年 5 月第 2 版 2004 年 8 月第 2 次 印刷 撰写人: 撰写日期:

大纲编号:S081400XJ004 数值分析 Numerical Analysis 课程编号:S081400XJ004课程属性:学科基础课 学时/学分:40/2 预修课程:微积分、线性代数、常微分方程、线性与非线性泛函分析初步 教学目的和要求: 科学课程为士木工程硕士研究生的学科基础课,同时也可作为物理、力学、化学及工 程科学等专业硕士研究生的选修课。本课程的主要内容包括:1.插值与数值积分的基本理 论:2.线性和非线性方程组的基本方法:3.离散动力系统与迭代法:4.线性与非线性特 征值问题:5.常微分方程数值解与有限元法简介。通过本课程的学习,希望学生掌握数值 分析的基本内容和基本方法,对数值分析的最新动态有初步了解,能运用所学方法上机实 算,为今后从事科学与工程计算打下基础 内容提要 第一章插值和数值积分 多项式与有理函数插值:三角函数与样条插值:Newton-Cotes型求积公式: Euler-Maclaurin求和公式:Gaussian型求积公式。 第二章线性与非线性方程组的基本方法 Gaus消去法:Cholesky分解:共轭梯度法:Lanczos算法:Newton法:Bairston法 多重网格法。 第三章离散动力系统的基本方法 重要背景和基本概念:Logestic模型:符号动力系统和拓扑共轭:Newton法:不动点 算法:Merrill法:同伦算法。 第四章线性和非线性特征值问愿的基本方法 Q算法:乘幂法与反幂法:子空间法代法:正则解的预估-校正算法:连续法。 第五章常微分方程数值解 常微分方程的基本理论:单步和多步法:刚性常微分方程简介:打靶法。 第六章变分原理与有限元法简介 变分原理:Euler方程:Ritz-Galerkin方法;有限元法简介。 教材: J.Stoer.R.Bulirsch.Introduction to Numerical Anahsis.Second Edition.Springer-Verlag.1991 主要参考书: 1.H.R.Schwarz,Numerical Analysis.A Comprehensive Introduction:With a Contribution by Chichester:Wiley,1989 2.蔡大用,白峰杉,《高等数值分析》,清华大学出版社,北京,1998 撰写人:曹礼群(数学与系统科学研究院) 撰写日期:2001年09日
大纲编号:S081400XJ004 数值分析 Numerical Analysis 课程编号: S081400XJ004 课程属性:学科基础课 学时/学分:40/2 预修课程:微积分、线性代数、常微分方程、线性与非线性泛函分析初步 教学目的和要求: 科学课程为土木工程硕士研究生的学科基础课,同时也可作为物理、力学、化学及工 程科学等专业硕士研究生的选修课。本课程的主要内容包括:1. 插值与数值积分的基本理 论;2. 线性和非线性方程组的基本方法;3. 离散动力系统与迭代法;4.线性与非线性特 征值问题;5. 常微分方程数值解与有限元法简介。通过本课程的学习,希望学生掌握数值 分析的基本内容和基本方法,对数值分析的最新动态有初步了解,能运用所学方法上机实 算,为今后从事科学与工程计算打下基础。 内容提要: 第一章 插值和数值积分 多项式与有理函数插值;三角函数与样条插值;Newton -Cotes 型求积公式; Euler-Maclaurin 求和公式;Gaussian 型求积公式。 第二章 线性与非线性方程组的基本方法 Gauss 消去法;Cholesky 分解;共轭梯度法;Lanczos 算法;Newton 法;Bairston 法; 多重网格法。 第三章 离散动力系统的基本方法 重要背景和基本概念;Logestic 模型;符号动力系统和拓扑共轭;Newton 法;不动点 算法;Merrill 法;同伦算法。 第四章 线性和非线性特征值问题的基本方法 QR 算法;乘幂法与反幂法;子空间迭代法;正则解的预估-校正算法;连续法。 第五章 常微分方程数值解 常微分方程的基本理论;单步和多步法;刚性常微分方程简介;打靶法。 第六章 变分原理与有限元法简介 变分原理;Euler 方程;Ritz-Galerkin 方法;有限元法简介。 教材: J. Stoer, R. Bulirsch,Introduction to Numerical Analysis, Second Edition, Springer-Verlag, 1991. 主要参考书: 1. H. R. Schwarz,Numerical Analysis,A Comprehensive Introduction: With a Contribution by J. Waldvogel, Chichester: Wiley,1989. 2. 蔡大用,白峰杉,《高等数值分析》,清华大学出版社,北京,1998。 撰写人:曹礼群(数学与系统科学研究院) 撰写日期:2001 年 09 日

大纲编号:S081400X005 数学物理方程 Differential Equations in Mathematical Physics 课程编号:S081400XJ005课程属性:学科基础课学时/学分:40/2 预悠课程:高等数学、常微分方程、线性代数、复变函数 教学目的和要求: 本课程为士木工程硕士研究生的学科基础课,同时也是电气工程学科硕士研究生的学科 基础课。主要介绍数学物理方程的基本知识和各种解法,提高学生解决实际问题的数学能力。 内容提要: 第一章定解问题 基本概念,三类基本方程,定解问题。 第二章行波法 Duhamel原理 一维波动问题,空间波动方程。 第三章分离变量法 分离变量法的一般原则,本征值问题,曲线坐标系,特殊函数。 第四章基本解方法 热传导方程的基本解和初值问题,波动方程的基本解和初值问题,场位方程第一,边 值问愿的格林函数 第五章变分法初步 泛函的极值问题,泛函的变分,欧拉方程,条件极值问题。 教材和主要参考书: 1.严镇军,《数学物理方程》,中国科学技术大学出版社,合肥,1996 2.郭敦仁,《数学物理方法》,人民教育出版社,北京,1977。 操写人:华士鸣(中国科学院研究生院) 操写日期:2001年09日
大纲编号:S081400XJ005 数学物理方程 Differential Equations in Mathematical Physics 课程编号: S081400XJ005 课程属性: 学科基础课 学时/学分: 40/2 预修课程: 高等数学、常微分方程、线性代数、复变函数 教学目的和要求: 本课程为土木工程硕士研究生的学科基础课,同时也是电气工程学科硕士研究生的学科 基础课。主要介绍数学物理方程的基本知识和各种解法,提高学生解决实际问题的数学能力。 内容提要: 第一章 定解问题 基本概念,三类基本方程,定解问题。 第二章 行波法 Duhamel 原理,一维波动问题,空间波动方程。 第三章 分离变量法 分离变量法的一般原则,本征值问题,曲线坐标系,特殊函数。 第四章 基本解方法 热传导方程的基本解和初值问题,波动方程的基本解和初值问题,场位方程第一,边 值问题的格林函数。 第五章 变分法初步 泛函的极值问题,泛函的变分,欧拉方程,条件极值问题。 教材和主要参考书: 1. 严镇军,《数学物理方程》,中国科学技术大学出版社,合肥,1996。 2. 郭敦仁,《数学物理方法》,人民教育出版社,北京,1977。 撰写人: 华士鸣(中国科学院研究生院) 撰写日期: 2001 年 09 日

大纲编号:S081400XJ006 随机过程 Stochastic Processes 课程编号:S081400XJ006 课程属性:学科基础课 学时/学分:40/2 预修课程:概率论、复变函数 教学目的和要求: 本课程为士木工程研究生的学科基础课。在现代科技诸多领域,例如物理、化学、生物 通信、机电、自动化、地震、海洋及经济等学科中均有者广泛的应用。本课程内容包括随机 过程的概念和基本类型、Markov链、Poisson过程、二阶矩过程、平稳过程及其谱分解、 Gauss过程、Brown运动、鞅及随机分析简介。通过本课程的学习,希望初步掌握随机过 程的基本概念、方法和技巧,为进一步学习其它后续课程及应用打下坚实的基础。内容提 要, 第一章随机过程简介及基础知识 随机过程概念与例子,概率空间,随机变量及分布函数,条件期望与概率生成函数, 特征函数与Laplace变换,随机变量收敛的概念和极限定理,熵和信息。 第二章Markov链 ,链的定义与例子,n步转移概率矩阵,强Markov性,状态空间的分解,常返 与瞬过,平稳分布,分支过程。 第三章Poisson过程 Poisson过程的定义与例子,Poisson过程基本性质,Poisson过程的一些推广。 第四章纯不连续Markov过程 纯不连续Markov过程的定义,Kolmogorov-.Feller方程,生灭过程,Q矩阵。 第五章二阶矩过程与随机分析简介 二阶矩过程及预备知识,均方极限、导数、积分,关于正交增量过程的随机积分,随 机积分和微分。 第大章平稳过程 平稳过程的定义与例子,平稳过程的谱分解,平稳过程的遍历性与采样定理,线性系 统中的平稳过程, AR Ap,q)模型简介 第七章Gaus过程与Brown运动 多元正态分布,Gaus过程,正态Markov过程,Brown运动的定义,Brown运动的 性质。 第八章鞅论简介 鞅的定义和一些例子,Doob停时停止定理,Dob上穿不等式及鞅的收敛性, 教材: 陆大,《随机过程及其应用》,清华大学出版社,北京,2000。 主要参考书: 1.复旦大学编,《概率论第三册:随机过程》,高等教育出版社,北京,1995。 2方兆本,零柏其,《克机讨程》.中国科学技术大学出版社,合肥,1992。 3.王梓坤,《随机过程》,科学出版社,北京,1996。 撰写人:张三国(中国科学院研究生院) 撰写日期:2001年09日
大纲编号:S081400XJ006 随机过程 Stochastic Processes 课程编号: S081400XJ006 课程属性:学科基础课 学时/学分:40/2 预修课程:概率论、复变函数 教学目的和要求: 本课程为土木工程研究生的学科基础课。在现代科技诸多领域,例如物理、化学、生物、 通信、机电、自动化、地震、海洋及经济等学科中均有着广泛的应用。本课程内容包括随机 过程的概念和基本类型、Markov 链、Poisson 过程、二阶矩过程、平稳过程及其谱分解、 Gauss 过程、Brown 运动、鞅及随机分析简介。通过本课程的学习,希望初步掌握随机过 程的基本概念、方法和技巧,为进一步学习其它后续课程及应用打下坚实的基础。内容提 要: 第一章 随机过程简介及基础知识 随机过程概念与例子,概率空间,随机变量及分布函数,条件期望与概率生成函数, 特征函数与 Laplace 变换,随机变量收敛的概念和极限定理,熵和信息。 第二章 Markov 链 Markov 链的定义与例子,n 步转移概率矩阵,强 Markov 性,状态空间的分解,常返 与瞬过,平稳分布,分支过程。 第三章 Poisson 过程 Poisson 过程的定义与例子,Poisson 过程基本性质,Poisson 过程的一些推广。 第四章 纯不连续 Markov 过程 纯不连续 Markov 过程的定义,Kolmogorov-Feller 方程,生灭过程,Q 矩阵。 第五章 二阶矩过程与随机分析简介 二阶矩过程及预备知识,均方极限、导数、积分,关于正交增量过程的随机积分,随 机积分和微分。 第六章 平稳过程 平稳过程的定义与例子,平稳过程的谱分解,平稳过程的遍历性与采样定理,线性系 统中的平稳过程,ARMA(p,q)模型简介。 第七章 Gauss 过程与 Brown 运动 多元正态分布,Gauss 过程,正态 Markov 过程,Brown 运动的定义,Brown 运动的 性质。 第八章 鞅论简介 鞅的定义和一些例子,Doob 停时停止定理,Doob 上穿不等式及鞅的收敛性。 教材: 陆大 ,《随机过程及其应用》,清华大学出版社,北京,2000。 主要参考书: 1. 复旦大学编,《概率论第三册:随机过程》,高等教育出版社,北京,1995。 2. 方兆本,缪柏其,《随机过程》,中国科学技术大学出版社,合肥,1992。 3. 王梓坤,《随机过程》,科学出版社,北京,1996。 撰写人: 张三国(中国科学院研究生院) 撰写日期: 2001 年 09 日