
Chapter 7 Vibration monitoring 7.1 Introduction The use of vibration data from rotating machinery to determine machine health has a long history. Traditionally the shop foreman would press the end of a screwdriver against a bearing housing and the handle against his ear, and in this way conduct the pure vibration signal from the bearing to be analysed in his brain. This proved so reliable over many decades that it was attempted to develop instruments which performed the same function but whose performance was reproducible and could function independently of the individual operator's skill and experience (Angelo, 1987). Initially vibration meters, reading an overall rms level of velocity, were introduced. Later on integration of accelerometer signals was introduced. This enabled rms estimates of acceleration, velocity and displacement to take place. The use of peak value and crest factor were also introduced. These estimates proved valuable but experienced operators could still identify incipient faults long before they were detected by these basic vibration meters(Angelo, 1987). The development of the FFT algorithm and affordable, portable, robust battery- powered FFT analysers, allowed the use of much more of the information embedded in the vibration signal and obtaining far more advanced and useful analyses. Today condition-based vibration monitoring has established itself as a reliable and cost effective technique for monitoring and diagnosing machinery faults before leading to irreversible damage, deterioration or unsafe catastrophic breakdowns. It renders signifi- cant benefits, including decreased maintenance costs, increased availability of machinery, reduced spare part stock holdings and improved safety. Condition monitoring involves the continuous or periodic assessment of the condition of a plant or a machine component while it is running, or of a structural component while in service. The maintenance interval is determined by the condition of a machine. This is quite different to a scheduled maintenance programme where a machine is serviced at a specific period in time irrespective of its condition, and a breakdown maintenance programme where a machine is run until it fails. Noise and vibration analysis is one of several condition monitoring techniques (albeit certainly the most widely applied). Other techniques include temperature monitoring, current and voltage monitoring, metallurgical failure analysis, and wear debris analysis. 1

2 CHAPTER 7.VIBRATION MONITORING This chapter is concerned with the usage of vibration as a diagnostic tool.Typical signal analysis techniques are reviewed.Procedures for source identification and fault detection from a variety of different vibration signals are developed. When machines are in a good condition,vibration frequency spectra have characteristic shapes.As faults begin to develop,the frequency spectra change.This is the fundamental basis for using vibration measurements and analysis in condition monitoring.Of course, sometimes the signal which is to be monitored is submerged within some other signal and it cannot be detected by a straightforward time history or spectral analysis.When this is the case,specialised signal processing techniques have to be utilised. 7.2 Vibration as a diagnostic tool Single overall(broadband)vibration measurements are useful for evaluating a machine's general condition.However,a detailed frequency analysis is generally necessary for di- agnostic purposes.Various frequency components in the vibration (or noise)frequency spectrum can often be related to certain rotational or reciprocating motions such as shaft rotational speeds,gear tooth meshing frequencies,bearing rotational frequencies,piston reciprocating motions,etc.These signals change in amplitude and/or frequency as a result of wear,eccentricity,unbalanced masses,etc.and can be readily monitored. As a general rule,machines do not break down without some form of warning-pending machine troubles are characterised by an increase in noise and/or vibration levels,and this is used as an indicator.The well known bathtub curve,illustrated in figure 7.1,is a plot of vibration versus time for a machine.The level decreases during the running- in period,increases very slowly during the normal operational duration as normal wear occurs,and finally increases very rapidly as it approaches a possible breakdown.If normal preventative maintenance repairs were performed,repairs would be carried out at specified fixed intervals irrespective of whether or not they were required.By delaying the repair until the monitored noise or vibration levels indicate a significant increase,unnecessary maintenance and 'strip-down'can be avoided.Not only does this minimise delays in production,but unnecessary errors during 'strip-down'which could produce further faults are avoided. Breakdown Repair performed Check intervals increased、 New machine Repair necessary Running-in check interval main enance Time Figure 7.1 The bathtub curve (from Norton,1989)

3 This technique of continuous 'on-condition'monitoring has three primary advantages. Firstly,it avoids catastrophic failures by shutting down a machine when noise or vibration levels reach a pre-determined level.Secondly,there are significant economic advantages as a result of increasing the running time between shut-downs.Thirdly,since the frequency spectrum of a machine in the normal running condition can be used as a reference signal for the machine,subsequent signals when compared with this signal allow for an identification of the source of the fault. The third advantage mentioned above is most important and needs some amplification. Although overall vibration measurements provide a good starting point for fault detection, frequency analysis provides much more information.In addition to diagnosing the fault, it gives an earlier indication of the development of the fault than an overall vibration measurement does.This is illustrated in figure 7.2 where early fault detection via the spectrum analysis results in an early warning. 1)Early fault detection early warning Log A Log f 2)Trend Analysis -determination of date of break down Log A Log A 2 vna ng on spectrum component 504t5 Figure 7.2 Trending frequency components (from Angelo,1987) The choice of a suitable location for the measurement transducer is also important As an illustrative example,consider the bearing housing in figure 7.3.The acceleration measurements are used to monitor the running condition of the shaft and bearing since wear usually occurs at the connection between rotating parts and the stationary support frame,i.e.at the bearings.The accelerometers must be placed such as to obtain as direct a path for vibration as is possible.If this is not the case then the measured signal will be contaminated'by the frequency response characteristics of the part and will not be a true representation of the source signal.Accelerometers A and C are positioned in a more direct path than B or D.Accelerometer C senses the vibration from the bearing more than vibration from other parts of the machine.Accelerometer D would receive a confusion of signals from the bearing and other machine parts.Likewise,accelerometer A is positioned

4 CHAPTER 7.VIBRATION MONITORING in a more direct path for axial vibrations than is accelerometer B. (suitable) B (not suitable (suitable) 0 (not suitable) Figure 7.3 Transducer location (from Norton,1989) In summary,vibration signals are utilised for condition monitoring because (i)a ma- chine running in good condition has a stable noise and vibration frequency spectrum- when the condition changes,the spectrum changes,and (ii)each component in the fre- quency spectrum can be related to a specific source within the machine.Thus,fault diagnosis depends on having a knowledge of the particular machine in question,i.e.shaft rotational speeds,number of gear teeth,bearing geometry,etc.This is illustrated schemat- ically in figure 7.4. Vibration Frequency [Hz] Figure 7.4 Relating frequency spectrum components to specific sources (from Angelo, 1987) 7.3 Signal analysis techniques When using vibration as a diagnostic tool,the type of signal analysis technique required depends very much upon the level of sophistication that is required to diagnose the prob- lem.Numerous analysis techniques are available for the condition monitoring of machinery or structural components with noise and vibration signals

5 Available signal analysis techniques are now reviewed with particular emphasis being placed upon their usage as a diagnostic tool.In condition monitoring,it is common to group magnitude and time domain analysis procedures together.This is essentially be- cause the magnitude parameters (rms values,peak values,skewness,etc.)are generally trended over an extended period of time.Thus,magnitude and time domain analysis techniques,are grouped together here.In addition to conventional time and frequency domain analysis techniques,advanced techniques like cepstrum analysis,sound intensity techniques for sound source location,envelope spectrum analysis,recovery of source sig- nals,and propagation path identification are reviewed in this section. 7.3.1 Time domain analysis techniques The analysis of individual time histories of vibration signals is in itself a very useful diagnostic procedure.Quite often,a significant amount of information can be extracted from a simple time history.For a start,the nature of the signal can be clearly identified -i.e.is it transient (impulsive),random or periodic.Furthermore,peak levels can be detected.Also,as vibration levels start to increase due to a deterioration of the condition of the equipment being monitored,the time history changes. Sometimes,when the dominant excitation source is a discrete frequency,it is necessary to phase-average a noise and/or vibration history.This is achieved by synchronising the signal to be measured with the excitation signal,i.e.the measurement is triggered at a specific point (usually a zero crossing)in the excitation cycle.This allows for the removal of unwanted random and periodic signal components.Signals which are synchronous with the trigger will average to their mean value while noise or non-synchronous signals will average to zero.Phase-averaging in the time domain is sometimes referred to as synchronous time-averaging. Several magnitude parameters can be extracted from the time history of a noise or vibration signal: Peak values Sometimes only an overall magnitude is required.This is especially true where it is only necessary to distinguish between acceptable and unsatisfactory states.Peak values of vibration are sometimes used for this purpose.These values are considered quite useful as long as essentially harmonic motion is considered (Broch,1980,p.21) The peak value vibration is the maximum value Xmaz of vibration during a given interval T.It is usually taken as the maximum deviation of that vibration from the mean value.A positive peak value is the maximum positive deviation and a negative peak value is the maximum negative deviation. The mean value may be defined by 元=心t (7.1) This value in itself has been found to be of limited practical interest(Broch,1980)

6 CHAPTER 7.VIBRATION MONITORING The peak-to-peak(P-P)value is often used and defined as the difference between the extreme values of the vibration.A zero-to-peak (0-P)value is defined as one-half of the peak-to-peak value. Root mean square value (rms) The rms value of a function x(t)over an interval T is T Xrms Jo x(t)2dt T (7.2) rms values are widely used in industry for general monitoring purposes but do not necessarily show appreciable changes in the early stages of bearing damage.Similarly the change in vibration energy caused by gear defects accounts for only a small proportion of the total vibration energy.Therefore diagnostic methods such as measuring the peak value or total rms is generally not sensitive to early faults (Liu,Chen Zhang,1991). High frequency detection(HFD) Indications of the initial stages of a bearing fault can however apparently be achieved by trending the peak or rms levels of the high frequency response(Kadushin,1991). The vibration signal is bandpass filtered from 5 kHz to 40 kHz.A bearing defect imposes an impact force on the system structure.The system acceleration response signal is often enhanced by the high frequency transducer resonance.The signal is then enveloped by means of full wave rectification.The HFD parameter is the overall value of either the peak or rms level of the time wave form.By trending this value it is possible to determine if the bearing requires lubrication or if a fault is developing (Kadushin,1991). Crest factor The crest factor is the ratio of the peak level to the rms level: CP=Xmaz Xrms (7.3) The crest factor is a measure of the impulsiveness of a vibration signal.It is often used when dealing with shocks,impulsive noise and short events.The crest factor for a sine wave is 1.414,and the crest factor for a truly random noise signal is generally less than 3. The crest factor is commonly used to detect impulsive vibrations produced by damaged bearings.As a rule of thumb,good bearings have vibration crest factors of about 2.5 to 3.5,and damaged bearings have crest factors >3.5.Values as high as 7 can sometimes be recorded prior to failure. Crest factors are reliable only in the presence of significant impulsiveness.Crest fac- tors of a vibration signal are relatively insensitive to operating speed and bearing load, provided sufficient speed is maintained to generate a bearing vibration which is above the background level,and sufficient load is applied to maintain full contact.At higher oper- ating speeds both the peak and the rms values increase proportionally,giving a relatively constant crest factor.In the absence of significant impulsiveness,the reliability of the

7 crest factor to detect bearing damage breaks down.Typical examples include bearings with shallow defects which have no significant edge,bearings with advanced damage and bearings with a large number of defects or widespread damage (Norton,1989). Probability density The probability density p()(see paragraph 4.2.2)of the bearing vibration acceleration has been suggested to give an indication of the bearing condition.The probability density of a bearing in good condition has a Gaussian distribution of accelerations,whereas a damaged bearing results in a non-Gaussian distribution with a dominant tail,because of a relative increase in the number of high levels of acceleration.However some authors have reported near-Gaussian distributions in some damaged bearings also (Tandon Nakra, 1992): This ties in with an observation by Braun and Hammond(1986)that the probability density is insensitive to many variations of the signal pattern. Kurtosis A series of statistical methods can be used to define the shape of the probability density distribution.The first two statistical moments of a probability density distribution are the mean value and the mean-square value(see paragraph 4.2.1).The third statistical moment is the skewness of a distribution,which is a measure of the symmetry of the probability density function.The fourth statistical moment is widely used in machinery diagnostics, particularly for rolling element bearings.It is called kurtosis,and it is given by kurtosis 职=ne=人a (7.4) Because the fourth power is involved,the value of kurtosis is weighted towards the values in the tails of the probability density distributions-i.e.it is related to the spread in the distribution.As a general rule,odd statistical moments provide information about the disposition of the peak relative to the median value,and even statistical moments provide information about the shape of the probability distribution curve.The value of kurtosis for a Gaussian distribution is 3.A higher kurtosis value indicates that there is a larger spread of higher values than would generally be the case for a Gaussian distribution. The kurtosis of a signal is very useful for detecting the presence of an impulse within the signal.It is widely used for detecting discrete,impulsive faults in rolling element bearings.Good bearings tend to have a kurtosis value of about 3,and bearings with impulsive defects tend to have higher values (generally >4).The usage of kurtosis is however limited because,as the damage to a bearing becomes distributed,the impulsive content of the signal decreases with a subsequent decrease in the kurtosis value.This
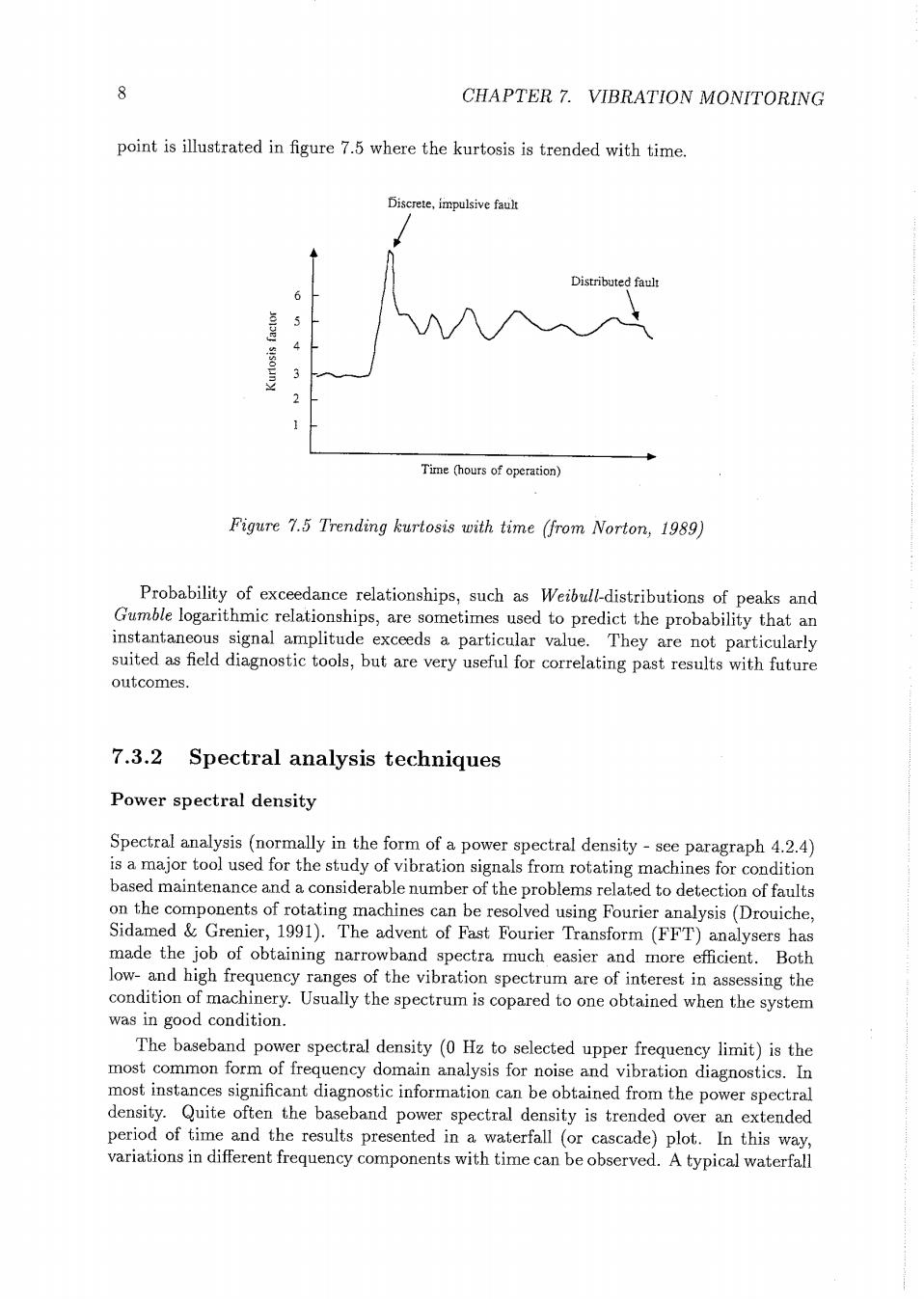
8 CHAPTER 7.VIBRATION MONITORING point is illustrated in figure 7.5 where the kurtosis is trended with time. Discrete,impulsive fault Distributed fault 5 4 Time (hours of operation) Figure 7.5 Trending kurtosis with time (from Norton,1989) Probability of exceedance relationships,such as Weibull-distributions of peaks and Gumble logarithmic relationships,are sometimes used to predict the probability that an instantaneous signal amplitude exceeds a particular value.They are not particularly suited as field diagnostic tools,but are very useful for correlating past results with future outcomes. 7.3.2 Spectral analysis techniques Power spectral density Spectral analysis (normally in the form of a power spectral density-see paragraph 4.2.4) is a major tool used for the study of vibration signals from rotating machines for condition based maintenance and a considerable number of the problems related to detection of faults on the components of rotating machines can be resolved using Fourier analysis(Drouiche, Sidamed Grenier,1991).The advent of Fast Fourier Transform(FFT)analysers has made the job of obtaining narrowband spectra much easier and more efficient.Both low-and high frequency ranges of the vibration spectrum are of interest in assessing the condition of machinery.Usually the spectrum is copared to one obtained when the system was in good condition. The baseband power spectral density(0 Hz to selected upper frequency limit)is the most common form of frequency domain analysis for noise and vibration diagnostics.In most instances significant diagnostic information can be obtained from the power spectral density.Quite often the baseband power spectral density is trended over an extended period of time and the results presented in a waterfall (or cascade)plot.In this way, variations in different frequency components with time can be observed.A typical waterfall

9 plot is illustrated in Figure 7.6. 10x 15x rpm orders 1kHz 2kHz Frequency Figure 7.6 Typical waterfall plot (from Heyns,1995) Zoom(passband)analysis is often used to provide detailed information within a spec- ified frequency band.Commercial analysers are available for specific passband frequency analysis applications.The shock pulse meter for monitoring ultrasonic frequency compo nents of high speed rolling element bearings is a typical example. Cepstrum analysis techniques Cepstrum analysis is the name given to a range of techniques involving functions which can be considered as a "spectrum of a logarithmic spectrum".Two types of cepstra exist the power cepstrum and the complex cepstrum.Both types of cepstra are real-valued functions. The power cepstrum is the inverse Fourier transform of the logarithm of the power spectrum(or the square of the modulus of the forward Fourier transform of the logarithm of the power spectrum)of a time signal.Both definitions are consistent with each other. It is mathematically defined by: Cp(T)=F-1{log1o Sz(w)} (7.5) Or Cp(T)=IF {1og1o S(w)}2 (7.6) The complex cepstrum is the inverse Fourier transform of the logarithm of the forward Fourier transform of a time signal and is mathematically defined as Ce =F-1 {log1o F{(t)}} (7.7) The power cepstrum is used to identify periodicity in the frequency spectrum,just like the frequency spectrum is used to identify periodicity in the time history of a signal.It is also used for echo detection and removal,for speech analysis,and for the measurement of properties of reflecting surfaces. The complex cepstrum is used when one wishes to edit (deconvolute)a signal in the frequency domain and subsequently return to the time domain.This procedure is possible because the complex cepstrum contains both magnitude and phase information

10 CHAPTER 7.VIBRATION MONITORING Since the effect of cepstrum is to compress whole families of harmonic frequencies to a single quefrency and perhaps one or two rahmonics,it seems to be an ideal parameter for sideband growth(Kim,Shin Carlson,1991).Most gear faults give a combination of amplitude and frequency modulation which lead to sidebands in the spectrum.The increase in number and strength of such sidebands usually indicates deteriorating condi- tion.Cepstrum has also been effectively applied for bearing diagnostics(Tandon Nakra, 1992) Cepstrum analysis is generally used as a complementary technique to spectral analysis. It is seldom used on its own as a diagnostic tool as it tends to suppress information about the global shape of the spectrum.Furthermore,the derivation of the cepstrum is not a routine signal analysis procedure,and one needs to exercise a certain amount of care. High-frequency resonance technique Envelope detection or High-Frequency Resonance Technique(HFRT)is an important sig- nal processing technique that helps in the identification of bearing defects by extracting characteristic fault frequencies (which may not be present in the direct spectrum)from the vibration signal of faulty bearings.Each time a defect in a rolling element bearing makes contact with another surface in the bearing,an impulse is generated.The impact excites resonance of the bearing elements,bearing housing,machine structure or trans- ducer.These resonances are excited periodically at the particular ball-pass frequency related to the location of the defect and are amplitude modulated at the characteristic fault frequency.By demodulating one of these resonances,a signal indicative of bearing condition can be recovered.In practice the signal is bandpass filtered around one of the resonant frequencies thus eliminating most of the vibration generated by shft imbalance, gear meshing or vibration from other parts of the machine.This bandpass-filtered signal consists of a narrowband carrier at the resonant frequency,which is amplitude modulated at the characteristic frequency.The signal is then demodulated by an envelope detector in which the signal is rectified and smoothed to eliminate the remaining components at the carrier frequency and its harmonics.The spectrum of the envelope signal is then obtained to get the characteristic defect frequency of the bearing.The resonant frequency best suited for the envelope detection technique has to be found experimentally by trying the technique at some of these major frequencies (Tandon Nakra,1992). The success of the method has been demonstrated by several investigators.The method works well for damage on outer races of bearings but not as well for inner races.Problems are also experienced with advanced damage in which case the defect frequencies may become submerged in the rising level of the spectrum. 7.3.3 Acoustic measurements Sound and ultrasound Measurement of the acoustic noise of a bearing has the attraction that it reflects more closely the response of the human ear.The detectability of defects by sound measurement may be affected by sources other than bearing noise unless adequate precautions have been taken to isolate the latter.A partial or full acoustic enclosure lined with sound absorbing