
第二篇 电力系统过电压及保护 2
2 第 二 篇 电力系统过电压及保护 电力系统过电压及保护

第12讲 线路和绕组中的波过程 无损耗单导线线路中的波过程 行波的折射与反射 行波通过串联电感和并联电容 行波的多次折、反射 无损平行多导线系统中的波过程 冲击电晕对线路波过程的影响
3 第 12 讲 线路和绕组中的波过程 线路和绕组中的波过程 无损耗单导线线路中的波过程 无损耗单导线线路中的波过程 行波的折射与反射 行波的折射与反射 行波通过串联电感和并联电容 行波通过串联电感和并联电容 行波的多次折、反射 行波的多次折、反射 无损平行多导线系统中的波过程 无损平行多导线系统中的波过程 冲击电晕对线路波过程的影响 冲击电晕对线路波过程的影响

第一节无损耗单导线 线路中的波过程 ■波过程的物理概念 ■波动方程及其解 ■前行波和反行波 ■波阻抗与波速 4
4 第一节 无损耗单导线 线路中的波过程 线路中的波过程 波过程的物理概念 波过程的物理概念 波动方程及其解 波动方程及其解 前行波和反行波 前行波和反行波 波阻抗与波速

第一节无损耗单导线线路中的波过程 1.波过程的物理概念 Lodx Lodx Lodx +X Codx Codx Codx 电源向电容充电,在导线周围建立起电 场,靠近电源的电容立即充电,并向相邻 的电容放电
5 1. 波过程的物理概念 波过程的物理概念 电源向电容充电,在导线周围建 电源向电容充电,在导线周围建立起电 场,靠近电源的电容立即充电,并向相邻 场,靠近电源的电容立即充电,并向相邻 的电容放电 第一节 无损耗单导线线路中的波过程 无损耗单导线线路中的波过程

Lodx Lodx Lodx X C E Codx Codx Codx ■ 由于电感作用,较远处电容需一段时间才能充上 一定的电荷,电压波以某速度沿线路x传播 随着线路电容的充放电,将有电流流过导线的电 感,在导线周围建立起磁场。电流波以同样速度 沿x方向流动 6
6 由于电感作用,较远处电容需一段时 由于电感作用,较远处电容需一段时间才能充上 一定的电荷,电压波以某速度沿线路 一定的电荷,电压波以某速度沿线路 x 传播 随着线路电容的充放电,将有电流流 随着线路电容的充放电,将有电流流过导线的电 感,在导线周围建立起磁场。电流波 感,在导线周围建立起磁场。电流波以同样速度 沿 x 方向流动

1.波过程的物理概念 电压波和电流波沿线路的流动,实际上就是 电磁波沿线路的传播过程 电压波和电流波的关系 电流波和电压波沿导线的传播过程实际上就 是电磁能量传播的过程 ()-GC)
7 1. 波过程的物理概念 波过程的物理概念 电压波和电流波沿线路的流动,实际上就是 电压波和电流波沿线路的流动,实际上就是 电磁波沿线路的传播过程 电磁波沿线路的传播过程 Z C L i u = = 0 0 电压波和电流波的关系 电压波和电流波的关系 2 0 2 0 ( ) 21 ( ) 21 vL ⋅i = vC ⋅u 电流波和电压波沿导线的传播过程实际上就 电流波和电压波沿导线的传播过程实际上就 是电磁能量传播的过程 是电磁能量传播的过程
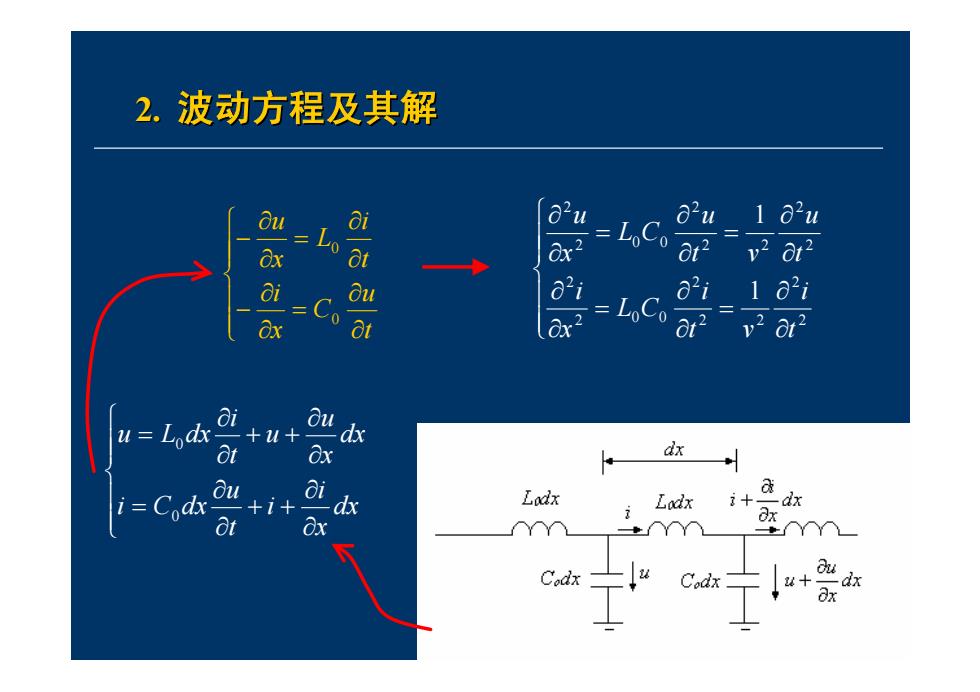
2.波动方程及其解 di Ou 1 O2u aa 8t a =Co =LoCo 1 821 dx t u=Lodx +2u+ u d 8x dx i=Codx +i+ -dx Lodx Lodx i+ -dx 8t Ex +YY C.dx Codx
8 2. 波动方程及其解 波动方程及其解 ⎪⎪⎩ ⎪⎪⎨⎧ ∂ ∂ = ∂ ∂ − ∂ ∂ = ∂ ∂ − t u C x i t i L x u 0 0 ⎪⎪⎩ ⎪⎪⎨⎧ ∂ ∂ = ∂ ∂ = ∂ ∂ ∂ ∂ = ∂ ∂ = ∂ ∂ 2 2 2 2 2 2 0 0 2 2 2 2 2 2 2 0 0 2 1 1 t i t v i L C x i t u t v u L C x u ⎪⎪⎩ ⎪⎪⎨⎧ ∂ ∂ + + ∂ ∂ = ∂ ∂ + + ∂ ∂ = dx x i i t u i C dx dx x u u t i u L dx 0 0

2.波动方程及其解 采用运算微积求解:拉氏变换 (x,t)台U(x,p),i(x,t)→I(x,p) dUp2=L,C.p"U(x,P) dx? 二阶齐次线性 'I(xP)=LCop'I(x.p) 常微分方程 dr2 U(x.p)-U,(ple+U,(p)e U,p小、Up I,p)、p I.D)=1(p+l(pe 由初始和边界条 件确定 9
9 采用运算微积求解: 采用运算微积求解:拉氏变换 u(x,t) ⇔ U(x, p),i(x,t) ⇔ I(x, p) ⎪⎪⎩ ⎪⎪⎨⎧ = = ( , ) ( , ) ( , ) ( , ) 2 2 0 0 2 2 2 0 0 2 L C p I x p dx d I x p L C p U x p dx d U x p 二阶齐次线性 常微分方程 ⎪⎩ ⎪⎨⎧ = + = + − − x p f x p q x p f x p q I x p I p e I p e U x p U p e U p e υ υ υ υ ( , ) ( ) ( ) ( , ) ( ) ( ) Uq (p)、 Uf (p) Iq (p) 、If (p) 由初始和边界条 由初始和边界条 件确定 2. 波动方程及其解 波动方程及其解 0 0 1 L C v =

2.波动方程及其解 根据拉氏变换的延迟定理 f)台F(p)+F(peP"⊙ft-T) x)=,-+4,+ (x0=0-+,0+ 变量置换 (x,t)=4,(x-Dr)+u,(x+Dr) i(x,t)=i,(x-vt)+i;(x+Dt) 10
10 根据拉氏变换的延迟定理 根据拉氏变换的延迟定理 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = − + + = − + + ( , ) ( ) ( ) ( , ) ( ) ( ) υ υ υ υ x i t x i x t i t x u t x u x t u t q f q f ⎪⎩ ⎪ ⎨ ⎧ = − + + = − + + ( , ) ( ) ( ) ( , ) ( ) ( ) i x t i x t i x t u x t u x t u x t q f q f υ υ υ υ f ( t ) ⇔ F ( p ) ( ) ( τ ) τ ⇔ − − F p e f t p 变量置换 2. 波动方程及其解 波动方程及其解
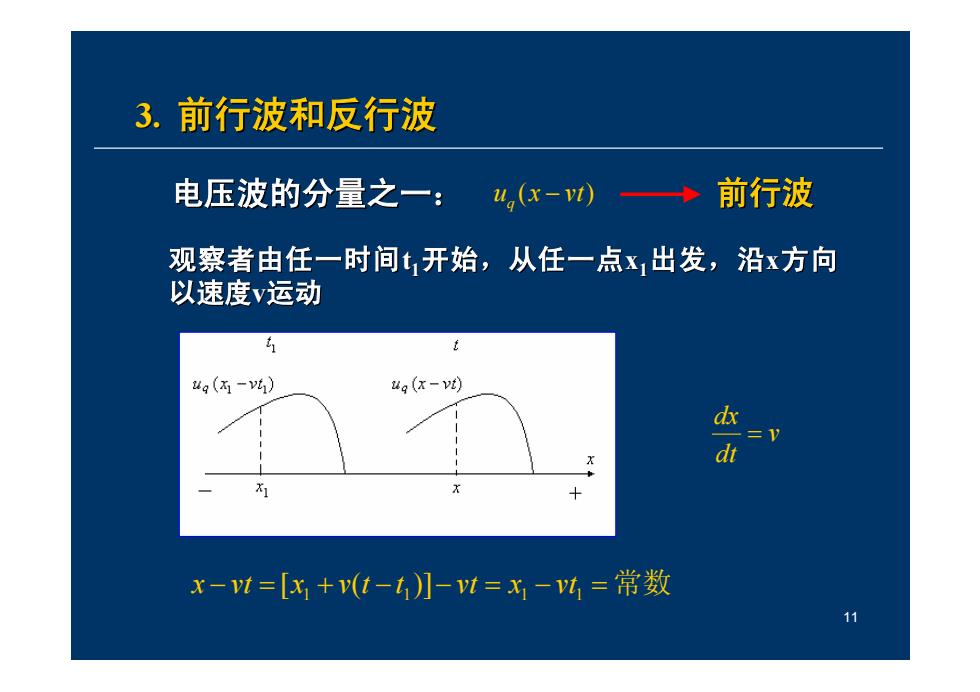
3.前行波和反行波 电压波的分量之一:u(x-v0 前行波 观察者由任一时间1开始,从任一点x出发,沿x方向 以速度v运动 g(3-v41) ug(x-vt) =1 dt x-vt=[x+vt-】-vt=x-V=常数 11
11 3. 前行波和反行波 前行波和反行波 x − vt = [x1 + v(t −t1)]− vt = x1 − vt1 = 常数 电压波的分量之一: 电压波的分量之一: u (x vt) q − 观察者由任一时间 观察者由任一时间t1开始,从任一点 开始,从任一点x1出发,沿x方向 以速度v运动 前行波 v dt dx =