
第五章 选择基础理论 ——质量性状选择方法 甘肃农业大学动物科学技术学院 Three periods
第五章 选择基础理论 ——质量性状选择方法 甘肃农业大学动物科学技术学院 Three periods

预备知识 特定基因型占群体内全部基因型的比率,叫做基因型频率 (genotype frequency)。 ▪ 假定二倍体生物一个常染色体座位A0,具有两个等位基因A 和a(设它们的频率分别为p和q)。根据孟德尔定律可知, 该座位会有三种不同的基因型AA、Aa和aa(设它们的频率 分别为D、H和R)。假如群体内AA和Aa个体的比例分别为 1/5和1/4,那么,它们相应的基因型频率就分别为0.20和 0.25。 ▪ 同一座位所有基因型频率之和等于1,即D + H + R = 1。 基因型频率 某一基因型个体数 总个体数 = 基因型频率
预备知识 特定基因型占群体内全部基因型的比率,叫做基因型频率 (genotype frequency)。 ▪ 假定二倍体生物一个常染色体座位A0,具有两个等位基因A 和a(设它们的频率分别为p和q)。根据孟德尔定律可知, 该座位会有三种不同的基因型AA、Aa和aa(设它们的频率 分别为D、H和R)。假如群体内AA和Aa个体的比例分别为 1/5和1/4,那么,它们相应的基因型频率就分别为0.20和 0.25。 ▪ 同一座位所有基因型频率之和等于1,即D + H + R = 1。 基因型频率 某一基因型个体数 总个体数 = 基因型频率

预备知识 特定基因座位一种等位基因占该座位全部等位 基因总数的比率。在二倍体生物中,完全显 性时,其计算公式为: 任何座位上全部等位基因频率之和都应等于1, 即p + q = 1。 显性基因的频率 ×显性个体数 杂合个体数 ×总个体数 隐性基因的频率 ×隐性个体数 杂合个体数 ×总个体数 = + = + 2 2 2 2 基因频率
预备知识 特定基因座位一种等位基因占该座位全部等位 基因总数的比率。在二倍体生物中,完全显 性时,其计算公式为: 任何座位上全部等位基因频率之和都应等于1, 即p + q = 1。 显性基因的频率 ×显性个体数 杂合个体数 ×总个体数 隐性基因的频率 ×隐性个体数 杂合个体数 ×总个体数 = + = + 2 2 2 2 基因频率
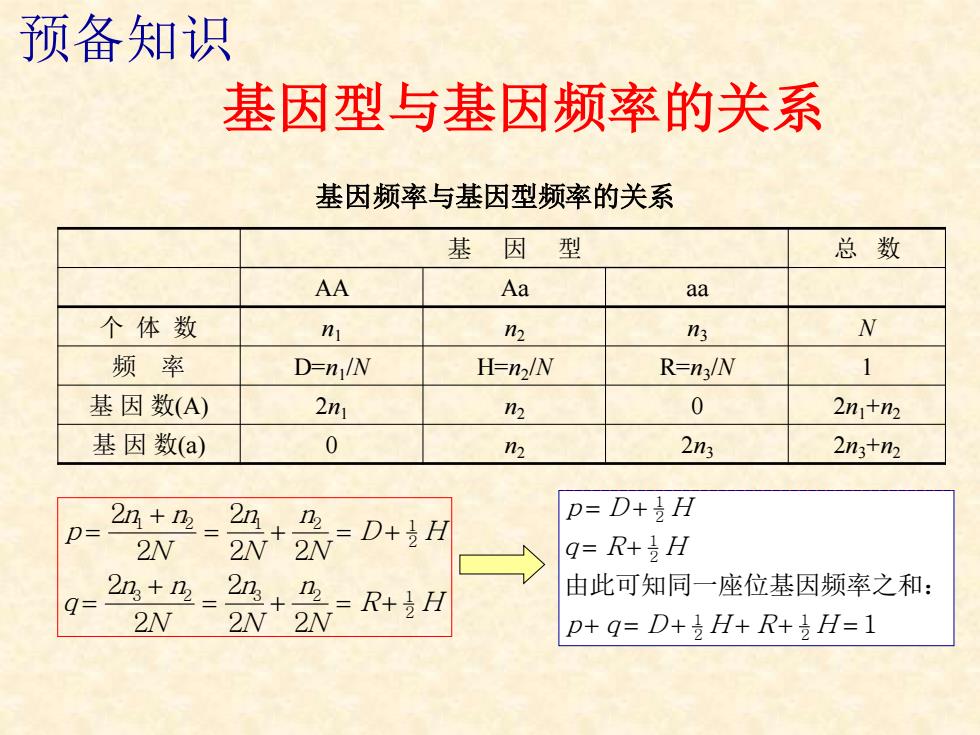
预备知识 基因频率与基因型频率的关系 基 因 型 总 数 AA Aa aa 个 体 数 n1 n2 n3 N 频 率 D=n1 /N H=n2 /N R=n3 /N 1 基 因 数(A) 2n1 n2 0 2n1+n2 基 因 数(a) 0 n2 2n3 2n3+n2 p n n N n N n N D H q n n N n N n N R H = + = + = + = + = + = + 2 2 2 2 2 2 2 2 2 2 1 2 1 2 1 2 3 2 3 2 1 2 p D H q R H p q D H R H = + = + + = + + + = 1 2 1 2 1 2 1 2 1 由此可知同一座位基因频率之和: 基因型与基因频率的关系
预备知识 基因频率与基因型频率的关系 基 因 型 总 数 AA Aa aa 个 体 数 n1 n2 n3 N 频 率 D=n1 /N H=n2 /N R=n3 /N 1 基 因 数(A) 2n1 n2 0 2n1+n2 基 因 数(a) 0 n2 2n3 2n3+n2 p n n N n N n N D H q n n N n N n N R H = + = + = + = + = + = + 2 2 2 2 2 2 2 2 2 2 1 2 1 2 1 2 3 2 3 2 1 2 p D H q R H p q D H R H = + = + + = + + + = 1 2 1 2 1 2 1 2 1 由此可知同一座位基因频率之和: 基因型与基因频率的关系

哈代——温伯格定律 英国数学家哈代(Hardy , G.H. , 1908)和德国医生温伯格(Weinberg , W. , 1909)于1908年和1909年各自独立提出了关于群体内基因频率和基因 型频率变化的定律。 要点: ①在随机交配的大群体中,若没有其它因素(如突变、迁移、选择等)的 影响,基因频率一代一代下去始终保持不变; ②任何一个大群体,无论其基因频率如何,只要经过一代随机交配,一对 常染色体基因的基因频率就达到平衡状态,没有其它因素的影响,以后一 代一代随机交配下去,这种平衡状态始终保持不变; ③在平衡状态下,基因型频率与基因频率的关系是: D= p 2 , H= 2pq , R= q 2 哈代——温伯格定律也叫遗传平衡定律(Law of genetic equilibrium)。 所谓遗传平衡是指群体中基因频率和基因型频率从一代到另一代保持不变 的现象。 前提条件: ①群体无限大;②随机交配;③没有突变;④没有迁移;⑤没有任何形式 的自然选择,那么群体中的基因频率和基因型频率从一代到另一代保持不 变。 预备知识
哈代——温伯格定律 英国数学家哈代(Hardy , G.H. , 1908)和德国医生温伯格(Weinberg , W. , 1909)于1908年和1909年各自独立提出了关于群体内基因频率和基因 型频率变化的定律。 要点: ①在随机交配的大群体中,若没有其它因素(如突变、迁移、选择等)的 影响,基因频率一代一代下去始终保持不变; ②任何一个大群体,无论其基因频率如何,只要经过一代随机交配,一对 常染色体基因的基因频率就达到平衡状态,没有其它因素的影响,以后一 代一代随机交配下去,这种平衡状态始终保持不变; ③在平衡状态下,基因型频率与基因频率的关系是: D= p 2 , H= 2pq , R= q 2 哈代——温伯格定律也叫遗传平衡定律(Law of genetic equilibrium)。 所谓遗传平衡是指群体中基因频率和基因型频率从一代到另一代保持不变 的现象。 前提条件: ①群体无限大;②随机交配;③没有突变;④没有迁移;⑤没有任何形式 的自然选择,那么群体中的基因频率和基因型频率从一代到另一代保持不 变。 预备知识
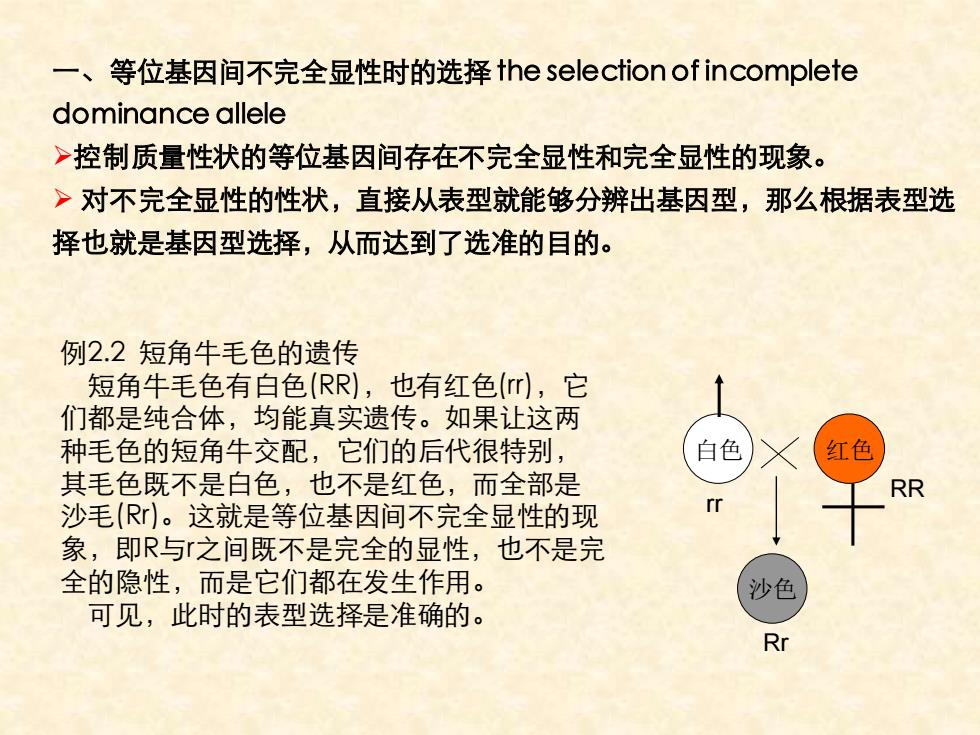
一、等位基因间不完全显性时的选择 the selection of incomplete dominance allele ➢控制质量性状的等位基因间存在不完全显性和完全显性的现象。 ➢ 对不完全显性的性状,直接从表型就能够分辨出基因型,那么根据表型选 择也就是基因型选择,从而达到了选准的目的。 例2.2 短角牛毛色的遗传 短角牛毛色有白色(RR),也有红色(rr),它 们都是纯合体,均能真实遗传。如果让这两 种毛色的短角牛交配,它们的后代很特别, 其毛色既不是白色,也不是红色,而全部是 沙毛(Rr)。这就是等位基因间不完全显性的现 象,即R与r之间既不是完全的显性,也不是完 全的隐性,而是它们都在发生作用。 可见,此时的表型选择是准确的。 白色 红色 沙色 rr RR Rr
一、等位基因间不完全显性时的选择 the selection of incomplete dominance allele ➢控制质量性状的等位基因间存在不完全显性和完全显性的现象。 ➢ 对不完全显性的性状,直接从表型就能够分辨出基因型,那么根据表型选 择也就是基因型选择,从而达到了选准的目的。 例2.2 短角牛毛色的遗传 短角牛毛色有白色(RR),也有红色(rr),它 们都是纯合体,均能真实遗传。如果让这两 种毛色的短角牛交配,它们的后代很特别, 其毛色既不是白色,也不是红色,而全部是 沙毛(Rr)。这就是等位基因间不完全显性的现 象,即R与r之间既不是完全的显性,也不是完 全的隐性,而是它们都在发生作用。 可见,此时的表型选择是准确的。 白色 红色 沙色 rr RR Rr

二、对隐性基因的选择 •对隐性基因的选择实际上是对显性基因的淘汰过程 •当显性基因的外显率是100%,且杂合子与显性纯合 子的表型相同时,则可以通过表型鉴别,一次性地 将显性基因全部淘汰 •但一次性淘汰的做法会使部分“高产基因”随之丢 失 •明智的育种策略是,在保证生产性能不下降的前提 下,逐步完成对隐性基因的选择
二、对隐性基因的选择 •对隐性基因的选择实际上是对显性基因的淘汰过程 •当显性基因的外显率是100%,且杂合子与显性纯合 子的表型相同时,则可以通过表型鉴别,一次性地 将显性基因全部淘汰 •但一次性淘汰的做法会使部分“高产基因”随之丢 失 •明智的育种策略是,在保证生产性能不下降的前提 下,逐步完成对隐性基因的选择

确定显性纯合子及杂合子:首先借助等位基因间的显隐性关系,区分显 性个体与隐性个体,然后通过测交进一步识别显性纯合体与显性杂合体, 即判断其基因型。 当淘汰率为S时基因频率的基本计算: 设一对等位基因A、a,它们所组成的基因型为AA、Aa和aa。A对a完全显性; AA和Aa表型相同,为显性性状。若以相同的淘汰率淘汰公畜和母畜中的一部分 显性类型;交配方式的确定又与这一对性状无关,也就是对于这一对性状来说, 交配是随机的;以隐性基因频率的变化作为选择进展的标志,并设原始群体的基 因型频率为:D=p2 ,H=2pq,R=q2;淘汰率为s,(1- s)即为留种率。于是得到 下表
确定显性纯合子及杂合子:首先借助等位基因间的显隐性关系,区分显 性个体与隐性个体,然后通过测交进一步识别显性纯合体与显性杂合体, 即判断其基因型。 当淘汰率为S时基因频率的基本计算: 设一对等位基因A、a,它们所组成的基因型为AA、Aa和aa。A对a完全显性; AA和Aa表型相同,为显性性状。若以相同的淘汰率淘汰公畜和母畜中的一部分 显性类型;交配方式的确定又与这一对性状无关,也就是对于这一对性状来说, 交配是随机的;以隐性基因频率的变化作为选择进展的标志,并设原始群体的基 因型频率为:D=p2 ,H=2pq,R=q2;淘汰率为s,(1- s)即为留种率。于是得到 下表
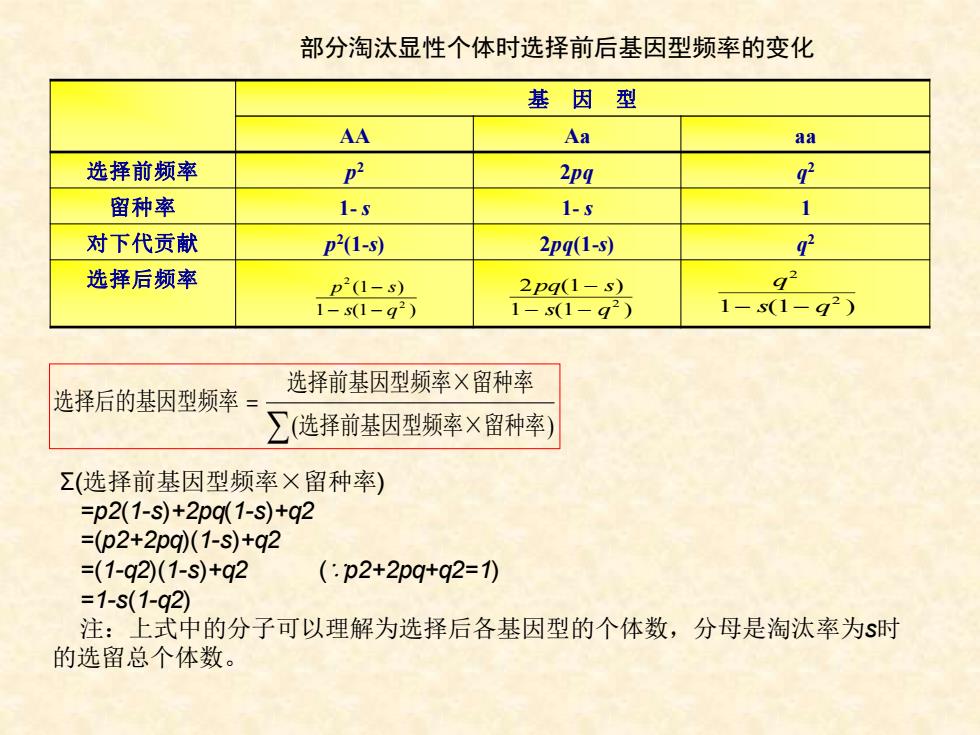
部分淘汰显性个体时选择前后基因型频率的变化 基 因 型 AA Aa aa 选择前频率 p 2 2pq q 2 留种率 1- s 1- s 1 对下代贡献 p 2 (1-s) 2pq(1-s) q 2 选择后频率 p s s q 2 2 1 1 1 ( ) ( ) − − − 2 1 1 1 2 pq s s q ( ) ( ) − − − q s q 2 2 1− (1− ) Σ(选择前基因型频率×留种率) =p2(1-s)+2pq(1-s)+q2 =(p2+2pq)(1-s)+q2 =(1-q2)(1-s)+q2 (∵p2+2pq+q2=1) =1-s(1-q2) 注:上式中的分子可以理解为选择后各基因型的个体数,分母是淘汰率为s时 的选留总个体数。 选择后的基因型频率 选择前基因型频率×留种率 选择前基因型频率×留种率 = ( )
部分淘汰显性个体时选择前后基因型频率的变化 基 因 型 AA Aa aa 选择前频率 p 2 2pq q 2 留种率 1- s 1- s 1 对下代贡献 p 2 (1-s) 2pq(1-s) q 2 选择后频率 p s s q 2 2 1 1 1 ( ) ( ) − − − 2 1 1 1 2 pq s s q ( ) ( ) − − − q s q 2 2 1− (1− ) Σ(选择前基因型频率×留种率) =p2(1-s)+2pq(1-s)+q2 =(p2+2pq)(1-s)+q2 =(1-q2)(1-s)+q2 (∵p2+2pq+q2=1) =1-s(1-q2) 注:上式中的分子可以理解为选择后各基因型的个体数,分母是淘汰率为s时 的选留总个体数。 选择后的基因型频率 选择前基因型频率×留种率 选择前基因型频率×留种率 = ( )

选择后实行随机交配。设选择后的基因型频率分别为D‘ 、H’、和R‘,则下一代 的基因频率q1为: q1=1/2H‘+R’ 利用这个公式,根据对显性类型的淘汰率,就可以计算下一代的隐性基因频率。 当s=1时(淘汰全部显性个体),则: 当s=0时(没有淘汰显性个体),则: q1=q 这就是说当全部淘汰显性个体时,只要没有突变,下一代隐性基因a的频率就可达 到1。可见选择隐性基因是相对容易的。但是,不完全淘汰显性个体时,下一代中 显性基因A还有一定的比例。 = − − − + − − = − + − − = − − + − − 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 pq s s q q s q pq s q s q q q s q s q ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − − − − = − − − − q s q q s q q q s q q s q ( ) ( ) ( ) ( ) ( . ) 2 2 1 2 2 1 1 1 1 2 2 q q q q q 1 2 2 1 1 = 1 − + − + =
选择后实行随机交配。设选择后的基因型频率分别为D‘ 、H’、和R‘,则下一代 的基因频率q1为: q1=1/2H‘+R’ 利用这个公式,根据对显性类型的淘汰率,就可以计算下一代的隐性基因频率。 当s=1时(淘汰全部显性个体),则: 当s=0时(没有淘汰显性个体),则: q1=q 这就是说当全部淘汰显性个体时,只要没有突变,下一代隐性基因a的频率就可达 到1。可见选择隐性基因是相对容易的。但是,不完全淘汰显性个体时,下一代中 显性基因A还有一定的比例。 = − − − + − − = − + − − = − − + − − 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 pq s s q q s q pq s q s q q q s q s q ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − − − − = − − − − q s q q s q q q s q q s q ( ) ( ) ( ) ( ) ( . ) 2 2 1 2 2 1 1 1 1 2 2 q q q q q 1 2 2 1 1 = 1 − + − + =