
2024/11/1 1 第五章 遗传基础理论 ——关于数量性状 甘肃农业大学动物科学技术学院 Two periods
2024/11/1 1 第五章 遗传基础理论 ——关于数量性状 甘肃农业大学动物科学技术学院 Two periods

2024/11/1 2 一、数量性状遗传基础 1、数量性状微效多基因假说 数量性状是由大量的、效应微小而类似的、并且可加的基因控制,这些 基因在世代相传中服从孟德尔原理,即分离规律和自由组合规律,以及连 锁交换规律。这些基因间一般没有明显的显隐性区别。此外,数量性状对 环境的影响相当敏感。 个体有限基因如何决定众多的数量性状? ➢“多因一效”和“一因多效”机制; ➢基因间的加性效应、等位基因间的显性效应和非等位基因间的上位 效应; ➢环境效应对数量性状的影响。 正因如此,有限基因所控制的数量性状表现出丰富的变异
2024/11/1 2 一、数量性状遗传基础 1、数量性状微效多基因假说 数量性状是由大量的、效应微小而类似的、并且可加的基因控制,这些 基因在世代相传中服从孟德尔原理,即分离规律和自由组合规律,以及连 锁交换规律。这些基因间一般没有明显的显隐性区别。此外,数量性状对 环境的影响相当敏感。 个体有限基因如何决定众多的数量性状? ➢“多因一效”和“一因多效”机制; ➢基因间的加性效应、等位基因间的显性效应和非等位基因间的上位 效应; ➢环境效应对数量性状的影响。 正因如此,有限基因所控制的数量性状表现出丰富的变异

2024/11/1 3 2、数量性状数学模型 P=G+E G=A+D+I E=EP+ET EP:持久环境效应,指时间上持久或空间上非局部的环境 因素,它影响个体的各次性状表现。 ET:暂时环境效应,一些暂时的、局部的环境因素只对个 体性状的某次度量值产生影响。由于此类效应有正有 负,当度量次数多时,这类效应可以相互抵消。 实际上,只有A可以真正遗传给后代,而D和I与E一样,不能稳定遗传, 因此,可以将D、I及E归为一类,即剩余值,用R表示,公式可变为:: P=A+R
2024/11/1 3 2、数量性状数学模型 P=G+E G=A+D+I E=EP+ET EP:持久环境效应,指时间上持久或空间上非局部的环境 因素,它影响个体的各次性状表现。 ET:暂时环境效应,一些暂时的、局部的环境因素只对个 体性状的某次度量值产生影响。由于此类效应有正有 负,当度量次数多时,这类效应可以相互抵消。 实际上,只有A可以真正遗传给后代,而D和I与E一样,不能稳定遗传, 因此,可以将D、I及E归为一类,即剩余值,用R表示,公式可变为:: P=A+R
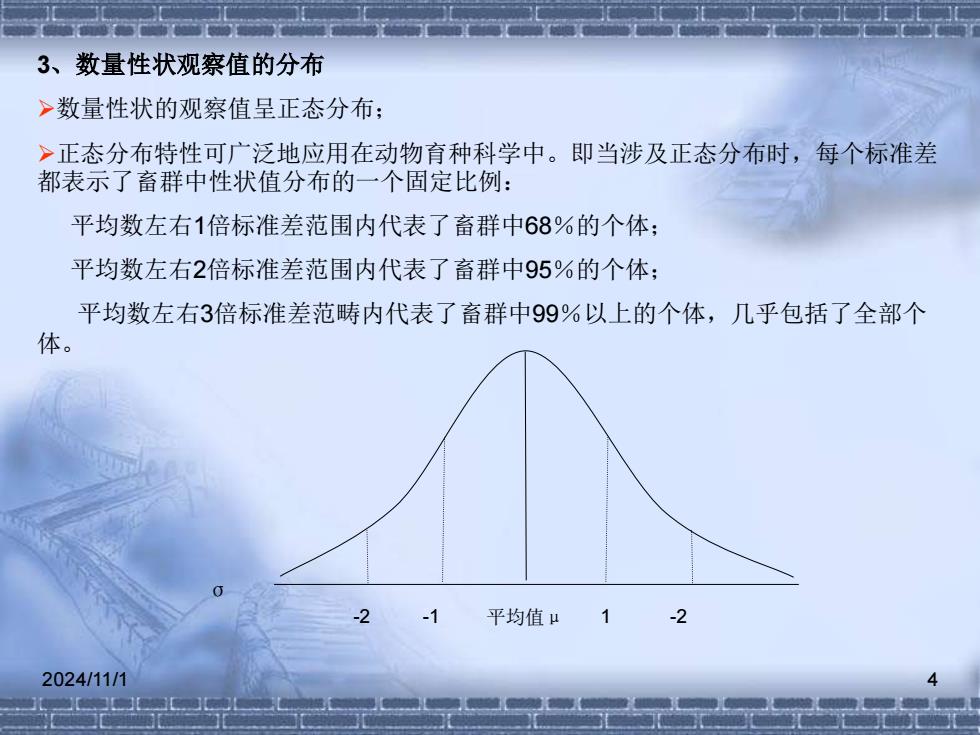
2024/11/1 4 3、数量性状观察值的分布 ➢数量性状的观察值呈正态分布; ➢正态分布特性可广泛地应用在动物育种科学中。即当涉及正态分布时,每个标准差 都表示了畜群中性状值分布的一个固定比例: 平均数左右1倍标准差范围内代表了畜群中68%的个体; 平均数左右2倍标准差范围内代表了畜群中95%的个体; 平均数左右3倍标准差范畴内代表了畜群中99%以上的个体,几乎包括了全部个 体。 平均值μ σ -2 -1 1 -2
2024/11/1 4 3、数量性状观察值的分布 ➢数量性状的观察值呈正态分布; ➢正态分布特性可广泛地应用在动物育种科学中。即当涉及正态分布时,每个标准差 都表示了畜群中性状值分布的一个固定比例: 平均数左右1倍标准差范围内代表了畜群中68%的个体; 平均数左右2倍标准差范围内代表了畜群中95%的个体; 平均数左右3倍标准差范畴内代表了畜群中99%以上的个体,几乎包括了全部个 体。 平均值μ σ -2 -1 1 -2

2024/11/1 5 例 应用正态分布的性质估计留种数和淘汰数 某品种成年奶山羊平均产奶量600 kg(泌乳期约8个月),产奶量的 表型标准差为100 kg 。要从1000只该品种成年母羊中,把奶量低于400 kg 的个体全部淘汰,那么可能要淘汰多少只? 解:产奶量低于400 kg 的个体,就是低于群体均值2倍标准差的个体: 600-2×100=400 kg 。2倍标准差以下的个体数:(1-0.95)/ 2= 0.025=2.5%。所以,从1000只该品种奶山羊中可能要淘汰25只产奶量 低于400 kg的个体。 若要从该群体中选出产奶量高于900 kg 的最优秀成年母羊,可能选出 几只?根据上面分析的同样道理:(1-0.99)/ 2=0.005 = 0.5%,所 以可知,最多能选出5只
2024/11/1 5 例 应用正态分布的性质估计留种数和淘汰数 某品种成年奶山羊平均产奶量600 kg(泌乳期约8个月),产奶量的 表型标准差为100 kg 。要从1000只该品种成年母羊中,把奶量低于400 kg 的个体全部淘汰,那么可能要淘汰多少只? 解:产奶量低于400 kg 的个体,就是低于群体均值2倍标准差的个体: 600-2×100=400 kg 。2倍标准差以下的个体数:(1-0.95)/ 2= 0.025=2.5%。所以,从1000只该品种奶山羊中可能要淘汰25只产奶量 低于400 kg的个体。 若要从该群体中选出产奶量高于900 kg 的最优秀成年母羊,可能选出 几只?根据上面分析的同样道理:(1-0.99)/ 2=0.005 = 0.5%,所 以可知,最多能选出5只

2024/11/1 6 4、祖先遗传定律和选择反应 19世纪生物统计学奠基人英国的高尔登(Galton , F. , 1876)在观察人 类身高对群体均值的关系中发现了数量性状遗传中的回归现象:如果双亲 身高在群体均值以上时,则后裔身高趋向高于群体均值,趋向低于双亲均 值(或称中亲值);如果双亲身高在群体均值以下,则后裔身高也趋向低 于群体均值,而趋向高于双亲均值。 大量材料都说明,后裔的平均表型值要比双亲均值更接近于群体均值。 也就是说,双亲均值高于或低于群体均值的数值,其中只有一部分能遗传 给子女,另一部分是由于环境影响,不能遗传。这说明后裔平均表型值有 向群体均值回归的现象。 Galton由此进一步引伸出取决于父母、祖父母、曾祖父母对后裔遗传影 响的概念,推导出一个祖先遗传定律的经验公式。此公式也为后来的一些 生物统计学家如皮尔逊(Pearson , K.)等所证实。到20世纪30年代,美 国的拉什(Lush , J. L.)首先把数量遗传应用于动物育种中,指出不同的数 量性状,其子女的表型均值对双亲均值的回归系数不同,由此提出了“遗 传力”的概念
2024/11/1 6 4、祖先遗传定律和选择反应 19世纪生物统计学奠基人英国的高尔登(Galton , F. , 1876)在观察人 类身高对群体均值的关系中发现了数量性状遗传中的回归现象:如果双亲 身高在群体均值以上时,则后裔身高趋向高于群体均值,趋向低于双亲均 值(或称中亲值);如果双亲身高在群体均值以下,则后裔身高也趋向低 于群体均值,而趋向高于双亲均值。 大量材料都说明,后裔的平均表型值要比双亲均值更接近于群体均值。 也就是说,双亲均值高于或低于群体均值的数值,其中只有一部分能遗传 给子女,另一部分是由于环境影响,不能遗传。这说明后裔平均表型值有 向群体均值回归的现象。 Galton由此进一步引伸出取决于父母、祖父母、曾祖父母对后裔遗传影 响的概念,推导出一个祖先遗传定律的经验公式。此公式也为后来的一些 生物统计学家如皮尔逊(Pearson , K.)等所证实。到20世纪30年代,美 国的拉什(Lush , J. L.)首先把数量遗传应用于动物育种中,指出不同的数 量性状,其子女的表型均值对双亲均值的回归系数不同,由此提出了“遗 传力”的概念

2024/11/1 7 二、数量性状遗传参数估计 1、重复力(repeatability) 一个数量性状在同一个体多次度量值之间相关程度。如同一奶牛不同泌 乳期产奶量间的相关(时间不同)、同一绵羊身体不同部位剪毛量间的相 关(空间不同)等。 对于同一性状不同时间、空间度量值间的相关,与其遗传因素与持久性 环境因素有关,因此,重复力可表示为: G E P ET G E P P G E P e V V V V V V V V r + + + = + = ➢重复力表示性状受遗传效应与持久环境效应影响的大小; ➢重复力高说明性状受暂时性环境效应影响小,每次度量值的代表性强, 因而所需度量的次数少; ➢重复力低说明性状受暂时性环境效应影响大,每次度量值的代表性差, 所需度量次数多
2024/11/1 7 二、数量性状遗传参数估计 1、重复力(repeatability) 一个数量性状在同一个体多次度量值之间相关程度。如同一奶牛不同泌 乳期产奶量间的相关(时间不同)、同一绵羊身体不同部位剪毛量间的相 关(空间不同)等。 对于同一性状不同时间、空间度量值间的相关,与其遗传因素与持久性 环境因素有关,因此,重复力可表示为: G E P ET G E P P G E P e V V V V V V V V r + + + = + = ➢重复力表示性状受遗传效应与持久环境效应影响的大小; ➢重复力高说明性状受暂时性环境效应影响小,每次度量值的代表性强, 因而所需度量的次数少; ➢重复力低说明性状受暂时性环境效应影响大,每次度量值的代表性差, 所需度量次数多

2024/11/1 8 2、遗传力(heritability) 广义:数量性状基因型方差占表型方差的比例。表示性状受遗传效应与环境效应影 响的大小。 狭义:数量性状育种值方差占表型方差的比例。 一般情况下,遗传力是指狭义遗传力,用公式表示为: A R A P 2 A V V V V V h + = = 从实际估计看,由于育种值无法直接度量,而表型值可以度量,因此从祖先遗传 定律可以得到:子女平均表型值对双亲均值的回归系数就等于遗传力,即: h 2 = bop (式中:h2为遗传力;bop为子女均值对双亲均值的回归系数。) 可以把子女均值(依变量)对双亲均值(自变量)的回归关系表达为: O = O + bOP (P − P) ( ) ( ) 2 O O h P P O O bOP P P − = − − = − P—任一双亲均值的数值; —全群双亲均值,实 际为亲代全群平均数; —子女均值的全群平均数, 也就是子代的全群平均数,对不作选择的群体 = ;O——与任一个双亲均值P相对应的子女均 值理论值。 P O P O
2024/11/1 8 2、遗传力(heritability) 广义:数量性状基因型方差占表型方差的比例。表示性状受遗传效应与环境效应影 响的大小。 狭义:数量性状育种值方差占表型方差的比例。 一般情况下,遗传力是指狭义遗传力,用公式表示为: A R A P 2 A V V V V V h + = = 从实际估计看,由于育种值无法直接度量,而表型值可以度量,因此从祖先遗传 定律可以得到:子女平均表型值对双亲均值的回归系数就等于遗传力,即: h 2 = bop (式中:h2为遗传力;bop为子女均值对双亲均值的回归系数。) 可以把子女均值(依变量)对双亲均值(自变量)的回归关系表达为: O = O + bOP (P − P) ( ) ( ) 2 O O h P P O O bOP P P − = − − = − P—任一双亲均值的数值; —全群双亲均值,实 际为亲代全群平均数; —子女均值的全群平均数, 也就是子代的全群平均数,对不作选择的群体 = ;O——与任一个双亲均值P相对应的子女均 值理论值。 P O P O

2024/11/1 9 3、遗传相关(genetic correlation) 相关性状 (correlated traits):动物的很多生产性能有着内在的联系。当 一个性状改变时,结果引起其它性状的变化,这种性状就称为相关性状。 性状间的相关也可区分为表型相关与遗传相关。 由于基因的一因多效和基因间的连锁不平衡造成的相关,即为遗传相关。 其中基因间连锁造成的相关,由于基因间的互换和丧失,由此造成的相关 也逐渐减少,这种相关也是不能稳定遗传的。由一因多效性造成的相关是 能稳定遗传的。 两个体由于所处相同环境造成的相关,称为环境相关,另外,由于等位基 因间的显性效应和上位效应造成的相关也不能真实遗传,因此,一般都并 入环境相关中,统称为剩余相关。 表型相关是由遗传和环境所引起的总相关。 奶 牛 rp ra 体重与体高 0.53 0.70 体重与产奶量 -0.044 -0.53 平均增重与产奶量 -0.05-0.27 0.19
2024/11/1 9 3、遗传相关(genetic correlation) 相关性状 (correlated traits):动物的很多生产性能有着内在的联系。当 一个性状改变时,结果引起其它性状的变化,这种性状就称为相关性状。 性状间的相关也可区分为表型相关与遗传相关。 由于基因的一因多效和基因间的连锁不平衡造成的相关,即为遗传相关。 其中基因间连锁造成的相关,由于基因间的互换和丧失,由此造成的相关 也逐渐减少,这种相关也是不能稳定遗传的。由一因多效性造成的相关是 能稳定遗传的。 两个体由于所处相同环境造成的相关,称为环境相关,另外,由于等位基 因间的显性效应和上位效应造成的相关也不能真实遗传,因此,一般都并 入环境相关中,统称为剩余相关。 表型相关是由遗传和环境所引起的总相关。 奶 牛 rp ra 体重与体高 0.53 0.70 体重与产奶量 -0.044 -0.53 平均增重与产奶量 -0.05-0.27 0.19

2024/11/1 10 三、影响数量性状选择效果的因素 1、数量性状的选择反应 ( ) 2 O −O = h P − P 表示选作种用的个体某性状表型值与供选择的初始群体该性状均值之差,简 单地讲,就是选留个体的均值与群体均值之差,这称为选择差(selection differential),用S表示之; 是选留个体的子女某性状表型平均值与供选择的初始群体的该性状均值之差 即子女均值高于全群均值的部分,或理解为由于选择而在下一代产生的反应,这称 为选择反应(selection response),也叫选择效应、选择响应,或遗传进展 (genetic advance),或遗传获得量(genetic gain),用R表示之。 P − P O−O 2 R = O−O = O− P = Sh 只要我们知道某一性状的遗传力,并决定选择差的大小,即可求出子代的遗传获得 量,也即,遗传获得量大小决定于h2和S。 遗传进展的快慢除决定于选择差和遗传力外,还受到世代间隔、选择性状的数目、 交配体系、遗传相关、培育等因素的影响
2024/11/1 10 三、影响数量性状选择效果的因素 1、数量性状的选择反应 ( ) 2 O −O = h P − P 表示选作种用的个体某性状表型值与供选择的初始群体该性状均值之差,简 单地讲,就是选留个体的均值与群体均值之差,这称为选择差(selection differential),用S表示之; 是选留个体的子女某性状表型平均值与供选择的初始群体的该性状均值之差 即子女均值高于全群均值的部分,或理解为由于选择而在下一代产生的反应,这称 为选择反应(selection response),也叫选择效应、选择响应,或遗传进展 (genetic advance),或遗传获得量(genetic gain),用R表示之。 P − P O−O 2 R = O−O = O− P = Sh 只要我们知道某一性状的遗传力,并决定选择差的大小,即可求出子代的遗传获得 量,也即,遗传获得量大小决定于h2和S。 遗传进展的快慢除决定于选择差和遗传力外,还受到世代间隔、选择性状的数目、 交配体系、遗传相关、培育等因素的影响