
第一章数字逻辑概论 ◆数字电路概述 在电子技术中,被传递和处理的信号 可分为模拟信号和数字信号两大类。本章 ◆数制与数码 之前所学的电路处理的是时间上和数值上 ◆逻辑门电路基础 均是连续变,化的模拟信号,属于模拟电路 的范畴。从第十章开始,所介绍的电路处 ◆本章小结 理的是时间上和数值上均是离散的、不连 续变化的脉冲数字信号,属于数字电路的 范畴。本章主要介绍数字电路的基础知识
在电子技术中,被传递和处理的信号 可分为模拟信号和数字信号两大类。本章 之前所学的电路处理的是时间上和数值上 均是连续变化的模拟信号,属于模拟电路 的范畴。从第十章开始,所介绍的电路处 理的是时间上和数值上均是离散的、不连 续变化的脉冲数字信号,属于数字电路的 范畴。本章主要介绍数字电路的基础知识。 数制与数码 逻辑门电路基础 数字电路概述 本章小结

第一节数字电路概述 数字电路的特点 电路结构简单,工作简单稳定可靠。 ◆数字电路抗干扰能力强。 ◆可以进行逻辑运算和判断。 ◆数字电路中元件处于开关状态,功耗较小。 由于数字电路具有上述特点,故发展十分迅速,在计算机、数字通信、 自动控制、数字仪器及家用电器等技术领域中得到广泛的应用
第一节 数字电路概述 一、数字电路的特点 电路结构简单,工作简单稳定可靠。 数字电路抗干扰能力强。 可以进行逻辑运算和判断。 数字电路中元件处于开关状态,功耗较小。 由于数字电路具有上述特点,故发展十分迅速,在计算机、数字通信、 自动控制、数字仪器及家用电器等技术领域中得到广泛的应用

二、脉冲信号 脉冲信号是指持续时间极短的电压或电流信号,常见的脉冲波形有:矩形波、 锯齿波、尖脉冲、阶梯波等。 几Π (a)矩形波 (b)锯齿波 ()尖脉冲 (d)阶梯波
二、脉冲信号 脉冲信号是指持续时间极短的电压或电流信号,常见的脉冲波形有:矩形波、 锯齿波、尖脉冲、阶梯波等。 (a)矩形波 (b)锯齿波 (c)尖脉冲 (d)阶梯波

●脉冲幅值Vm表示脉冲电压的最大值,其 值等于脉冲底部至脉冲顶部之间的电位差。 ◆脉冲上升时间t,表示脉冲前沿从0.1Vm上 升到Q9Vm所需的时间。 。脉冲下降时间t表示脉冲后沿从0.9'm下 降到0.1Vm所需的时间。 0.9Vm ●脉冲宽度tw由脉冲前沿0.5Vm到脉冲后沿 0.5V 0.5Vm之间的时间。 0.1Vm ●脉冲周期T对于周期性脉冲,脉冲周期指 相邻两脉冲波对应点之间的间隔时间,其倒 致k冲的频钉即了习 矩形脉冲主要参教 古空比D 脉冲宽度写脉冲周期T之比 称为占空比,即D= T
脉冲幅值Vm 表示脉冲电压的最大值,其 值等于脉冲底部至脉冲顶部之间的电位差。 脉冲上升时间tr 表示脉冲前沿从0.1Vm上 升到0.9Vm所需的时间。 脉冲下降时间tf 表示脉冲后沿从0.9Vm下 降到0.1Vm所需的时间。 脉冲宽度tw 由脉冲前沿0.5Vm到脉冲后沿 0.5Vm之间的时间。 脉冲周期T 对于周期性脉冲,脉冲周期指 相邻两脉冲波对应点之间的间隔时间,其倒 数为脉冲的频率f ,即 。 占空比D 脉冲宽度tw与脉冲周期T之比, 称为占空比,即 T t D w 矩形脉冲主要参数 T f 1
三、数字信号 通常把脉冲的出现或消失用1和0来表示,这样一串脉冲就变成由一串1和 Q组成的代码,这种信号称为数字信号。 数字信号 需注意的是数字信号的0和1并不表示数量的大小,而是代表电路的工作状 态,如开关、二极管、三极管导通用1状态表示;反之,器件截止时就用0 状态表示。 若规定高电平(3~5V)为逻辑1,低电平00.4V0为逻辑0,称为正逻辑 反之,若规定高电平为逻辑0,低电平为逻辑1,则称为负逻楫
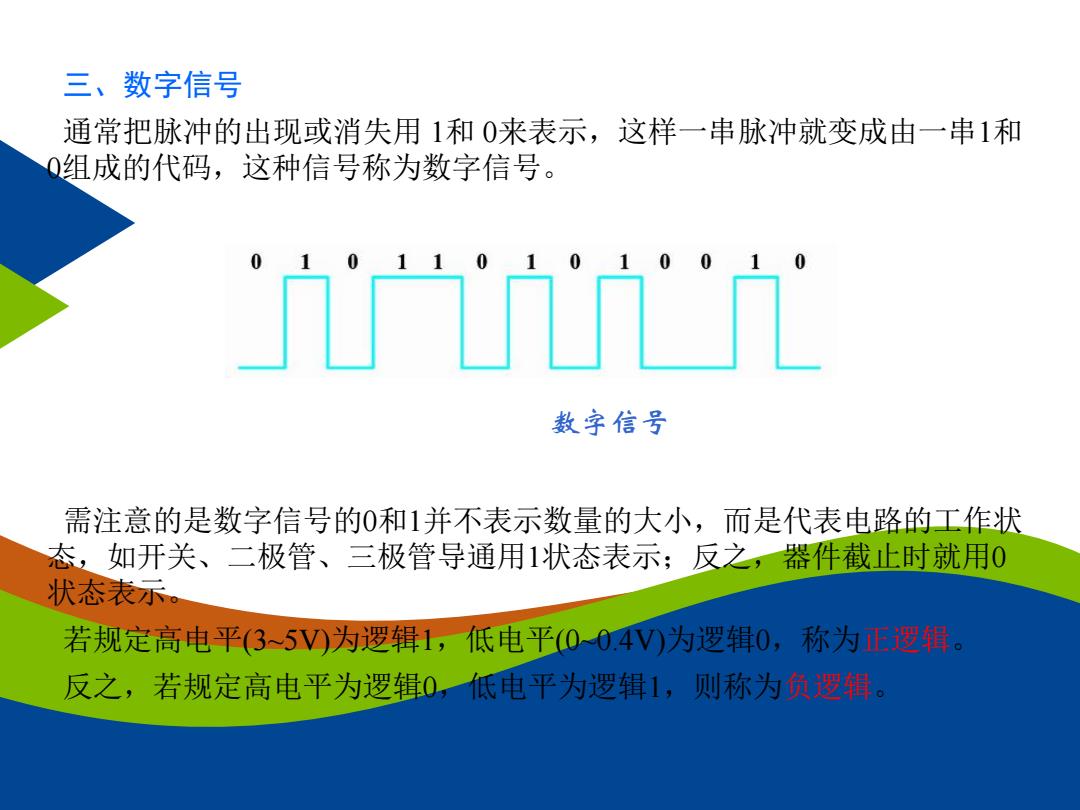
三、数字信号 通常把脉冲的出现或消失用 1和 0来表示,这样一串脉冲就变成由一串1和 0组成的代码,这种信号称为数字信号。 数字信号 需注意的是数字信号的0和1并不表示数量的大小,而是代表电路的工作状 态,如开关、二极管、三极管导通用1状态表示;反之,器件截止时就用0 状态表示。 若规定高电平(3~5V)为逻辑1,低电平(0~0.4V)为逻辑0,称为正逻辑。 反之,若规定高电平为逻辑0,低电平为逻辑1,则称为负逻辑

第二节RC电路的应用 一、RC微分电路 C微分电路是一种常用的波形变换电路,能够将矩形脉冲波变换 成尖脉冲。通常用来作为触发器、计数器、开关电路的触发信号。 输入波形 Vm 0 输出波形 0 微分电路 微分电路波形图 RC微分电路的输出波形要形成尖脉冲必须具备以下条件:电路的 时间常数=RC应远小手矩形波脉冲宽度, 即T《 通常,当x≤t时,可以认为满足条件
第二节 RC电路的应用 一、RC 微分电路 RC微分电路是一种常用的波形变换电路,能够将矩形脉冲波变换 成尖脉冲。通常用来作为触发器、计数器、开关电路的触发信号。 微分电路 微分电路波形图 RC微分电路的输出波形要形成尖脉冲必须具备以下条件:电路的 时间常数τ=RC应远小于矩形波脉冲宽度tw,即τ« tw。 通常,当τ≤tw时,可以认为满足条件
二、RC积分电路 RC积分电路也是一种常用的波形变换电路,它可以把矩形波变换成锯齿波。 RC积分电路通常用来作为数字电路的延时器、定时器的定时元件,在电视 机中可利用积分电路从复合行、场同步信号中取出场同步脉冲。 输入波形 C 输出波形 0 和分电路 和分电路波形图 积分电路要求电路的C时间常数应远大于脉冲宽度t,即》t,。 通常,当工≥3时,可以认为满足条件
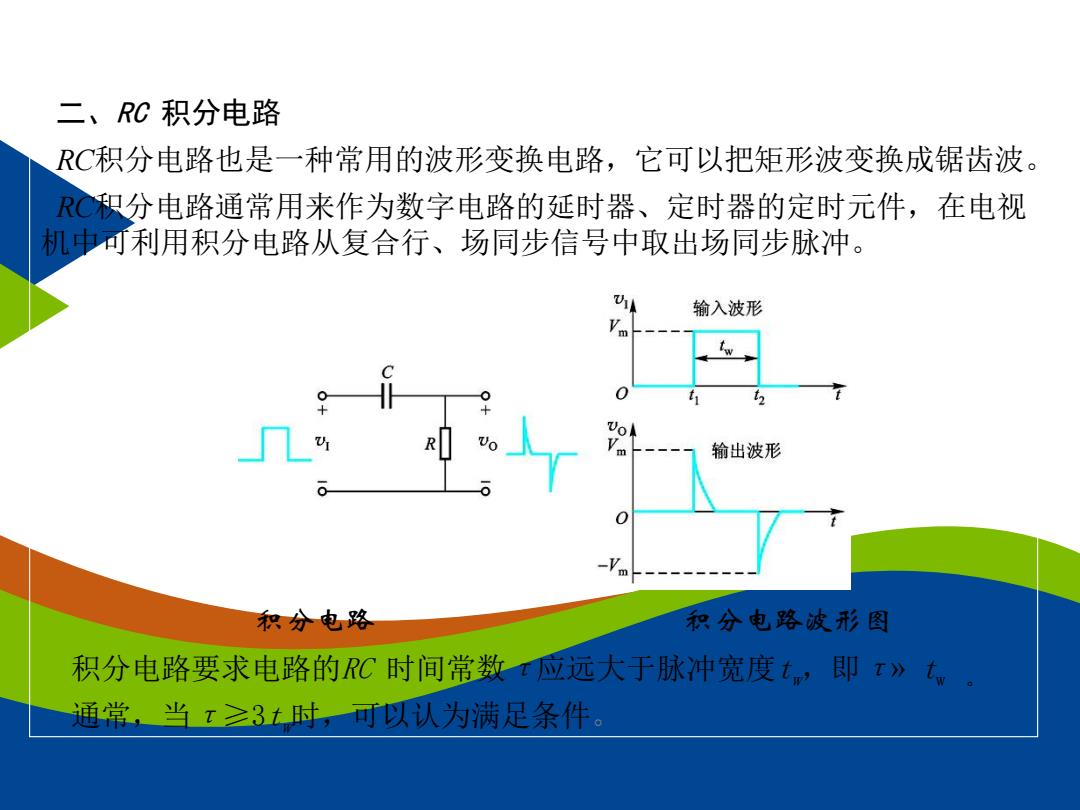
二、RC 积分电路 RC积分电路也是一种常用的波形变换电路,它可以把矩形波变换成锯齿波。 RC积分电路通常用来作为数字电路的延时器、定时器的定时元件,在电视 机中可利用积分电路从复合行、场同步信号中取出场同步脉冲。 积分电路 积分电路波形图 积分电路要求电路的RC 时间常数τ应远大于脉冲宽度tw,即τ» tw 。 通常,当τ≥3tw时,可以认为满足条件

第三节数制与码制 一、数制 选取一定的进位规则,用多位数码来表示某个数的值,这就 是所谓的数制。 1,十进制数 十进制数有0,1,2,3,4,5,6,7,8,9共十个符号,我们 称这些符号为数码。十进制数运算加法时遵循“逢十进一” 减法时遵循“借一当十”。 十进制数中,数码的位置不同,所表示的值就不相同,分个位、 十位、百位..,如: (N)10=km-1X10m-1+km-2×10m-2+…+k1×101+kX100+k1×10-1+k2×10-2+.. 十进制数用数学式表示的通式为:
第三节 数制与码制 一、数制 选取一定的进位规则,用多位数码来表示某个数的值,这就 是所谓的数制。 1.十进制数 十进制数有0,1,2,3,4,5,6,7,8,9共十个符号,我们 称这些符号为数码。十进制数运算加法时遵循“逢十进一” , 减法时遵循“借一当十” 。 十进制数中,数码的位置不同,所表示的值就不相同,分个位、 十位、百位…,如: (268.56)10=2×10 2+6×10 1+8×10 0+5×10 -1+6×10 -2 十进制数用数学式表示的通式为: (N)10=kn-1×10 n-1+kn-2×10 n-2+…+k1×10 1+k0×10 0+k-1×10 -1+k-2×10 -2+…

2.二进制数 二进制数仅有0和1两个不同的数码。进位规则为“逢二进 一”;借位规则为“借一当二”。对于任意一个二进制数可表 示为: (N)2=kn1X2m-1+km-2X2n-2+..+k1X21+kX20+k1X2-1+k2X2-2+. 例如,二进制数(10110.1) 2=1×24+0×23+1×22+1×21+0×20+1×2-1 3.十六进制 十六进制是“逢十六进一”,十六进制有0、1、2、3、4、5、 6、7、8、9、A、B、C、D、E、F共16个不同的数码。 例如,十六进制数(3AE)16=3×162+A×161+E×160 =3×162+10×161+14×160 与十进制对应的二进制、十六进制 十进制数 0 2 3 4 5 6 8 10 12 13 14 15 二进制数 0000 0001 00t0 001 0100 010h 0110 1000 100h 1010 101h 1100 1101 110 十六进制数 0 2 3 5 6 9 B
2 . 二进制数 二进制数仅有0和1两个不同的数码。进位规则为“逢二进 一” ;借位规则为“借一当二” 。对于任意一个二进制数可表 示为: 例如,二进制数(10110.1) 2 =1×2 4+0×2 3+1×2 2+1×2 1+0×2 0+1×2 -1 3.十六进制 十六进制是“逢十六进一” ,十六进制有0、1、2、3、4、5、 6、7、8、9、A、B、C、D、E、F共16个不同的数码。 例如,十六进制数(3AE) 16 =3×16 2+A×16 1+E×16 0 =3×16 2+10×16 1+14×16 0 与十进制对应的二进制、十六进制 (N)2=kn-1×2 n-1+kn-2×2 n-2+…+k1×2 1+k0×2 0+k-1×2 -1+k-2×2 -2+… 十进制数 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 二进制数 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 十六进制数 0 1 2 3 4 5 6 7 8 9 A B C D E F

4.不同数制的转换 (1)二进制数转换为十进制数转换方法是:把二进制数按 权展开,再把每一位的位值相加,即可得到相应的十进制数。 例题将二进制(101)2转化为十进制数。 :(101)2=1×22+0×21+1×20=(5)10 (2)十进制整数转换为二进制数转换方法是:把十进制数 逐次地用2除取余数,一直除到商数为零。然后将先取出的余 数作为二进数的最低位数码。 例题将十进制数19转化为二进制数 解: 219 29 余1,即k=1 2L4 余1,即k1=1 22 余0,即k2=0 21 余0,即k3=0 0 余1,即k4=1 所以(19)=(kkkk,)g(10011)2
4.不同数制的转换 (1)二进制数转换为十进制数 转换方法是:把二进制数按 权展开,再把每一位的位值相加,即可得到相应的十进制数。 例题 将二进制(101) 2转化为十进制数。 解:(101) 2 =1×2 2+0×2 1+1×2 0=(5) 10 (2)十进制整数转换为二进制数 转换方法是:把十进制数 逐次地用2除取余数,一直除到商数为零。然后将先取出的余 数作为二进数的最低位数码。 例题 将十进制数19转化为二进制数 解: 所以(19)10 =(k4k3k2k1k0)2 =(10011)2