
电路分析简介 向学生澄清以下定义。 E=直流电压。E=矢量电压。v用=时变电压。1,I和i)=电流。 ●基本物理量 限长的细导线之间产生每米2×10?牛顿 无功功率在负载下不会转换为热能。R(P) 的力所需的电流。它也等于1库仑/秒。 在无源电路中始终为正值。 可以根据基本S1单位或派生量进行验证的 特性。 电容(派生量)(C)-1法拉等于电压为1伏 能量(派生量)但-1焦耳相当于在1牛 特时能够储存1库仑电荷的电容器的大小。 顿力(kgm/sec的作用下移动1米所消 库仑(派生量)©)-1安培秒。大约 C=Q/V 耗的能量 624×108个电子所带的电荷。一个电子 电感(派生量)心一电感等于电路中的磁 或者 所带的电荷为1.6×10-℃。 通量与流过该电路的电流之比。 电压(派生量)(W或E)-1伏特等于通 J=P(t)dr 过1安培电流时为产生1瓦特负载所需的 L=/I 电动势(EM日. 1千瓦时等于3.6×10°焦耳。 当通过闭合回路的电流以1安培/秒的速 电阻(派生量)-1欧姆等于通过1安 度变化时,1亨利电感可以提供1伏特的 频率(派生量)一频率①是波形周期① 培电流时为产生1伏特电压所需的电阻。 电压。 的倒数。周期是信号重复出现的时间间隔 F=1T。角颜率的公式为 电流(基本量)①-这是S单位的一个基 功率(派生量)仰-1瓦特相当于每秒消 本标准,是在间隔1米的两根平行的、无 耗1焦耳的功率值。通常定义为下=E引。 0=2πf ●常规用法 电流方向一工程惯例指的是从电源的正极 电路中常常出现的寄生效应和非最佳的材 (+)端流向负极()端。这与电子流向相反 料问题 电子学中具有特殊含义的一些术语或概念。 但允许其他一些惯例仍然有效。 Q 节点一在示意图或电路图中,电路中多 开路一无电流通过的电路。 个支路的连接点。也可能指的是无电位差 的点。 短路一电压没有变化的电路。 支路一在示意图或电路图中,具有单独电 分贝dB- 流通路的一系列元件。 频域一如果我们定义了谐振频率和质量 灵敏度dB= 系数(注意.在谐振 接地一 101og )可以接地的那部分电路,或无电流通过 1 的安全电源连接。或者 0L= 就电压和电流而言常常用分贝表示。由于 @C 2)不必换算为接地的给定电路的任意基准。 电压和电流两者与功率都是平方关系,因 中。可能存在各种快捷算法),那么 此以dB表示这些物理量时需要将以上方 负载一耗损功率或改变输入功率、但不产 谐振频率一 程式乘以2。 生功率的那部分电路! 简谐共振一在具有并联PLC元件的交流 电源一能够产生功率的那部分电路。 电路中,阻尼描述了与消耗的能量相比存 LC 储在电路中的能量。在纯电阻电路中,存 储的能量为零。无功电路(包含电容器和 ①0是以弧度/秒表示的谐振频率。它是由 /或感应器的电路)可以瞬时存储能量以 电感和电容决定的,而与电阻无关。 备以后使用。注意:以下分析不包括实际 Tektronix Enabllng Innovatlon
基本物理量 可以根据基本 SI 单位或派生量进行验证的 特性。 库仑(派生量)(C) - 1 安培秒。大约 6.24 × 1018 个电子所带的电荷。一个电子 所带的电荷为 1.6 × 10-19C。 电压(派生量)(V 或 E)- 1 伏特等于通 过 1 安培电流时为产生 1 瓦特负载所需的 电动势 (EMF)。 电阻(派生量)(R) - 1 欧姆等于通过 1 安 培电流时为产生 1 伏特电压所需的电阻。 电流(基本量)(I) - 这是 SI 单位的一个基 本标准,是在间隔 1 米的两根平行的、无 限长的细导线之间产生每米 2 × 10-7 牛顿 的力所需的电流。它也等于 1 库仑/秒。 电容(派生量)(C) - 1 法拉等于电压为 1 伏 特时能够储存 1 库仑电荷的电容器的大小。 C = Q / V 电感(派生量)(L) - 电感等于电路中的磁 通量与流过该电路的电流之比。 当通过闭合回路的电流以 1 安培/秒的速 度变化时,1 亨利电感可以提供 1 伏特的 电压。 功率(派生量)(P) - 1 瓦特相当于每秒消 耗 1 焦耳的功率值。通常定义为 。 无功功率在负载下不会转换为热能。 在无源电路中始终为正值。 能量(派生量)(E) - 1 焦耳相当于在 1 牛 顿力 (kg m/sec2 ) 的作用下移动 1 米所消 耗的能量。 或者 1 千瓦时等于 3.6 × 106 焦耳。 频率(派生量) - 频率 (f) 是波形周期 (T) 的倒数。周期是信号重复出现的时间间隔。 F = 1/T。角频率的公式为 ▼ 电路分析简介 向学生澄清以下定义。 E = 直流电压。 = 矢量电压。v (t) = 时变电压。I、 和 i (t) = 电流。 常规用法 电子学中具有特殊含义的一些术语或概念。 节点 - 在示意图或电路图中,电路中多 个支路的连接点。也可能指的是无电位差 的点。 支路 - 在示意图或电路图中,具有单独电 流通路的一系列元件。 接地 - 1) 可以接地的那部分电路,或无电流通过 的安全电源连接。或者, 2) 不必换算为接地的给定电路的任意基准。 负载 - 耗损功率或改变输入功率、但不产 生功率的那部分电路。 电源 - 能够产生功率的那部分电路。 电流方向 - 工程惯例指的是从电源的正极 (+) 端流向负极 (-) 端。这与电子流向相反, 但允许其他一些惯例仍然有效。 开路 - 无电流通过的电路。 短路 - 电压没有变化的电路。 分贝 (dB) - 灵敏度 dB = , 就电压和电流而言常常用分贝表示。由于 电压和电流两者与功率都是平方关系,因 此以 dB 表示这些物理量时需要将以上方 程式乘以 2。 简谐共振 - 在具有并联 RLC 元件的交流 电路中,阻尼描述了与消耗的能量相比存 储在电路中的能量。在纯电阻电路中,存 储的能量为零。无功电路(包含电容器和 /或感应器的电路)可以瞬时存储能量以 备以后使用。注意:以下分析不包括实际 电路中常常出现的寄生效应和非最佳的材 料问题。 频域 - 如果我们定义了谐振频率和质量 系数(注意,在谐振 中,可能存在各种快捷算法),那么 谐振频率 - 是以弧度/秒表示的谐振频率。它是由 电感和电容决定的,而与电阻无关。 ▼

品质因素一 该公式假定最终形式为 过阻尼电路无振荡.但也需要花费过多时 间逐渐达到终值。 R O=- s2+ =0 v(1)=Ae+Ae" L或 O=@RC RC+LC 使用二次方程式求根。根据判别式有两个 其中 以上公式适用于并联谐振。对于串联谐振, 实根。一个根或两个复根即可确定阻尼。 为该值的倒数。 列出的变量A和P取决于初始条件。 Q是一个循环周期内存储的能量与耗损的 欠阻尼一 1 能量之比。基本上,它暗示了谐振系统中 的循环能量(在谐振系统外可能不明显)。 2RC 0o 20 dt2 RCdt LC 2RC ·无源元件 电容一电容是电路中平行金属板积蓄电荷 指数式衰减一 倾向的测量值。实际上没有直流电流通过 有关无源元件的基础知识说明。 12 只是电荷进出平行金属板.从而出现随着 欧姆定律-E=忆其中:乙是电阻(正 电压变化电子迁移的现象。 ×轴)元件与电感(oL)和电容1)复 dv(t) 合元件的矢量和。 (t)= i(dt或i(t)=C dt 379% 由于1厅等于.因此求阻抗之和时.电容 0.2 14% 电感一电感是表示电路或元件阻止改变电 5% 使用虚平面上的负y轴.电感使用正y轴。 0 2% 电塑电是-, 流的属性的测量值。 tau v(t)=Ldi(t) 电阻是阻碍电流流动的导体的属性。它将 dt 标准的RL或RC时间常数是指数式衰减 耗损有功功率。此处使用的例图包括了要 的。上图显示了当t为时间常数T时的残 识别的物理量。另外还有计算该物理量的 余振幅。 方程式。将I和R相乘可计算得出E。E 除以R可计算得出I。 数字逻辑 And/Nand-只有所有输入都为1.And函Or-只要任意一个输入为1.Or函数就会 数才会输出1。Nand是And的互补函数。 输出1。 A*B A*B ⊙ A+B A+B 运算符一下面说明了标准的布尔运算符。 And,Or和nvet为基本运算符。Nand,0 0 0 0 0 0 Nor.Xor和Xnor为派生运算符。Nand和 Nor常用于硬件中。Xor和Xnor在运算电 0 1 0 0 入 路中很有用。 1 0 0 0 0 2
数字逻辑 运算符 - 下面说明了标准的布尔运算符。 And、Or 和 Invert 为基本运算符。Nand、 Nor、Xor 和 Xnor 为派生运算符。Nand 和 Nor 常用于硬件中。Xor 和 Xnor 在运算电 路中很有用。 And/Nand - 只有所有输入都为 1,And 函 数才会输出 1。Nand 是 And 的互补函数。 A B A * B 0001 0101 1001 1110 Or - 只要任意一个输入为 1,Or 函数就会 输出 1。 A B A + B 0001 0110 1010 1110 ▼ 品质因素 - 或 以上公式适用于并联谐振。对于串联谐振, 为该值的倒数。 Q 是一个循环周期内存储的能量与耗损的 能量之比。基本上,它暗示了谐振系统中 的循环能量(在谐振系统外可能不明显)。 这样在串联谐振电路中无功元件上的电压 和并联谐振电路中通过无功元件的电流, 可能远远超过所有电阻元件上可见的电压 和电流。Q 也等于中心频率与 -3 dB 带宽 之比。 带宽 - 无功电路的带宽等于响应以 3 dB 变化的两处的频率差值。在直流仍为满增 益的位置,为上面的 3 dB 点。定义与电 路拓扑有关,而不管电流或电压是否为测 量的参数。 时域 - 计算电路时域响应的方法是写下该 电路的方程式,假定一些初始条件,然后 解微分方程式。 该公式假定最终形式为 使用二次方程式求根。根据判别式有两个 实根,一个根或两个复根即可确定阻尼。 列出的变量 An 和 取决于初始条件。 欠阻尼 - 低衰减电路通常会产生振荡,可能需要过 多的时间才能达到终值。 其中: 过阻尼 - 过阻尼电路无振荡,但也需要花费过多时 间逐渐达到终值。 其中: 临界阻尼 - 临界阻尼电路在可能的最短时间内达到终 值。以下情况下,会出现临界阻尼: 其中: 无源元件 有关无源元件的基础知识说明。 欧姆定律 - 其中: 是电阻(正 x 轴)元件与电感 和电容 复 合元件的矢量和。 由于 1/j 等于 -j,因此求阻抗之和时,电容 使用虚平面上的负 y 轴,电感使用正 y 轴。 电阻/电导 - 电阻是阻碍电流流动的导体的属性。它将 耗损有功功率。此处使用的例图包括了要 识别的物理量。另外还有计算该物理量的 方程式。将 I 和 R 相乘可计算得出 E。E 除以 R 可计算得出 I。 电容 - 电容是电路中平行金属板积蓄电荷 倾向的测量值。实际上没有直流电流通过, 只是电荷进出平行金属板,从而出现随着 电压变化电子迁移的现象。 或 电感 - 电感是表示电路或元件阻止改变电 流的属性的测量值。 指数式衰减 - 标准的 RL 或 RC 时间常数是指数式衰减 的。上图显示了当 t 为时间常数 τ 时的残 余振幅。 ▼ 和 2
ver一只要输入为0,Invert函数就会输公理-以下是两个基本的布尔代数公理。 结合律一 出1。 应注意此处的语义。布尔代数虽然在方法上 类似于数学代数,但定义不同。例如,以下 (A+B)+C=A+(B+C) 列出的布尔代数的分配律与数学代数的分配 (A'B)C=A(B*C) 律就不同。必须记住,“+”与“*”符号在 布尔代数和数学代数中的含义有本质上的区 定理一 0 别.因此某些情况下必须区别对待。 以下定理很有用,而且可以通过公理进行 Xor/Xnor(exclusive or/nor)-只要有一个且仅 证明。 交换律一 有一个输入为1.则Xor函数输出1。Xno 分配律一 是Xor的互补函数。 A+B=B+A A B A⊕B A*(B+C)=(A'B)+(A'C) A⊕B A'B=B'A 0 0 A+(B*C)=(A+B)"(A+C) 0 0 0 摩根定理一 0 0 (A+B)=A*B 1 0 1 (A*B)=A+B P元件 轴向引线元件 径向引线元件 ●颜色代码 黑色 褐色 精度:无20%.银10%.金5% 红色 2 橙色 值=(10*D1+D210 黄色 4 绿色 5 如果指数为银.则指数值为-2。如果为金 则指数值为-1。 蓝色 6 紫色 7 1%和更精确的电阻器使用四种色带来表 灰色 8 白色 9 示值。 电感器和电容器有时使用色带或色点来表 示值。 。标准电阻器值 有关精密电阻器的信息,请参阅 10 11121315161820 并非每个可能的电阻器值在实际中都可用。 http://www.vishay.com/docs/31001/dectable.pdf 以下是5%的标准值。以黑色表示的是 22 24273033363943 电感器和电容器通常使用相同的序列。但 10%的标准值。以灰色表示的是20%的标 47 51566268758291 常常只使用灰色框中的值。 准值。 ·分析技术 节点分析一针对有N个节点的电流使用节 4)解方程。如果电路包括电感和电容.则 点分析,可以列出有N1个未知量的N-1 需要微分方程。 下面介绍了一些基于基本原理的标准分析 元方程组并进行求解。将一个节点定义为 技术。 接地点,无需对其进一步求解。其它所有 网孔分析一使用网孔分析.可以列出有 分析都是相对于该参考接地点的 N-1未知量的N-1元方程组并进行求解。 基尔霍夫电压定律一稳态情况下,电路中 (为何是N-1个?因为组成一个网孔需要两 任一回路的电压和恒等于零。根据绕行的 步骤」 个节点。) 方向,电源为正极,所有其他元件为负极。 )写下电压电源上那些节点的节点电压。 如果这些元件为Z而非,那么必须多加 以下是一些方程式。 步骤 注意,但结果仍然正确。 1)写下网孔。对它们进行标记。确保网孔 (x=Va1-V2.此处x是N1和N2之间电压 是二维的。 电源的值) 2)写下电流电源。 2)将电压电源短路。由于原来未连接的两个 节点连在了一起,所以减少了节点数。为 ③)断开电流电源。有关基本原理.请参阅 何要进行该操作呢?请参阅“电源变换。 “电源变换”。 基尔霍夫电流定律一同样。一个节点所有 4)写出剩余每个回路的方程式。由于只剩 流入(或流出)的电流之和必须等于零。 ③)写出剩余节点的KCL方程式,并用电压 下电压电源和阻抗,因此电流必须通过 如果存在无阻抗元件,则应多加注意,但 除以阻抗的形式表示电流。此时应列出 电压和阻抗来表示。 结果依旧。 了在第1步和第3步定义的节点间的 N-1个方程式。 5)解前面列出的方程。如果电路包括电感 和电容。则需要微分方程。 3
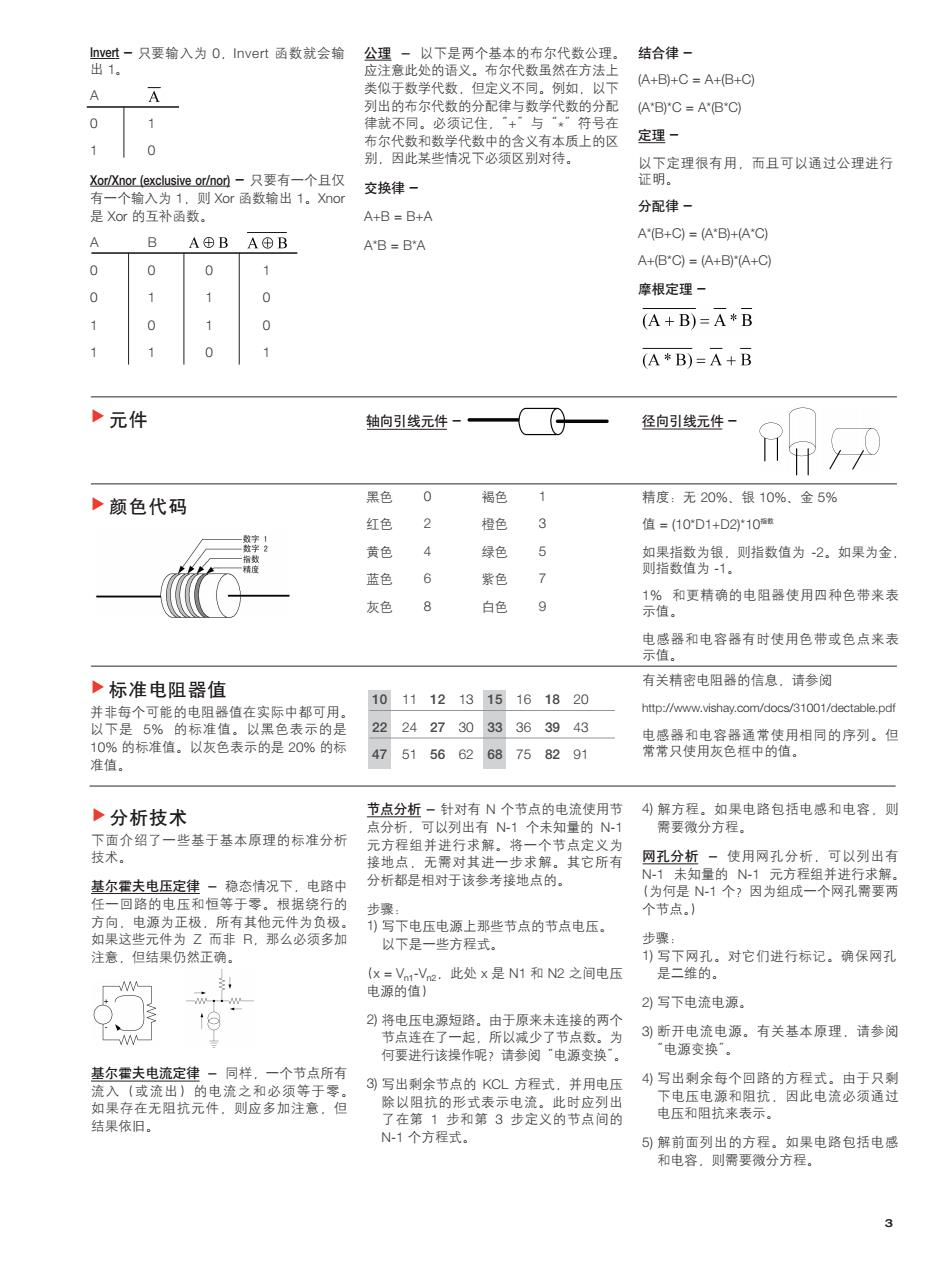
Invert - 只要输入为 0,Invert 函数就会输 出 1。 A 0 1 1 0 Xor/Xnor (exclusive or/nor) - 只要有一个且仅 有一个输入为 1,则 Xor 函数输出 1。Xnor 是 Xor 的互补函数。 A B 0001 0110 1010 1101 公理 - 以下是两个基本的布尔代数公理。 应注意此处的语义。布尔代数虽然在方法上 类似于数学代数,但定义不同。例如,以下 列出的布尔代数的分配律与数学代数的分配 律就不同。必须记住,“+”与“* ”符号在 布尔代数和数学代数中的含义有本质上的区 别,因此某些情况下必须区别对待。 交换律 - A+B = B+A A*B = B*A 结合律 - (A+B)+C = A+(B+C) (A*B)*C = A*(B*C) 定理 - 以下定理很有用,而且可以通过公理进行 证明。 分配律 - A*(B+C) = (A*B)+(A*C) A+(B*C) = (A+B)*(A+C) 摩根定理 - ▼ 元件 轴向引线元件 - 径向引线元件 - 颜色代码 黑色 0 褐色 1 红色 2 橙色 3 黄色 4 绿色 5 蓝色 6 紫色 7 灰色 8 白色 9 精度:无 20%、银 10%、金 5% 值 = (10*D1+D2)*10指数 如果指数为银,则指数值为 -2。如果为金, 则指数值为 -1。 1% 和更精确的电阻器使用四种色带来表 示值。 电感器和电容器有时使用色带或色点来表 示值。 ▼ 标准电阻器值 并非每个可能的电阻器值在实际中都可用。 以下是 5% 的标准值。以黑色表示的是 10% 的标准值。以灰色表示的是 20% 的标 准值。 有关精密电阻器的信息,请参阅 http://www.vishay.com/docs/31001/dectable.pdf 电感器和电容器通常使用相同的序列。但 常常只使用灰色框中的值。 ▼ 10 11 12 13 15 16 18 20 22 24 27 30 33 36 39 43 47 51 56 62 68 75 82 91 分析技术 下面介绍了一些基于基本原理的标准分析 技术。 基尔霍夫电压定律 - 稳态情况下,电路中 任一回路的电压和恒等于零。根据绕行的 方向,电源为正极,所有其他元件为负极。 如果这些元件为 Z 而非 R,那么必须多加 注意,但结果仍然正确。 基尔霍夫电流定律 - 同样,一个节点所有 流入(或流出)的电流之和必须等于零。 如果存在无阻抗元件,则应多加注意,但 结果依旧。 节点分析 - 针对有 N 个节点的电流使用节 点分析,可以列出有 N-1 个未知量的 N-1 元方程组并进行求解。将一个节点定义为 接地点,无需对其进一步求解。其它所有 分析都是相对于该参考接地点的。 步骤: 1) 写下电压电源上那些节点的节点电压。 以下是一些方程式。 (x = Vn1-Vn2,此处 x 是 N1 和 N2 之间电压 电源的值) 2) 将电压电源短路。由于原来未连接的两个 节点连在了一起,所以减少了节点数。为 何要进行该操作呢?请参阅“电源变换”。 3) 写出剩余节点的 KCL 方程式,并用电压 除以阻抗的形式表示电流。此时应列出 了在第 1 步和第 3 步定义的节点间的 N-1 个方程式。 4) 解方程。如果电路包括电感和电容,则 需要微分方程。 网孔分析 - 使用网孔分析,可以列出有 N-1 未知量的 N-1 元方程组并进行求解。 (为何是 N-1 个?因为组成一个网孔需要两 个节点。) 步骤: 1) 写下网孔。对它们进行标记。确保网孔 是二维的。 2) 写下电流电源。 3) 断开电流电源。有关基本原理,请参阅 “电源变换”。 4) 写出剩余每个回路的方程式。由于只剩 下电压电源和阻抗,因此电流必须通过 电压和阻抗来表示。 5) 解前面列出的方程。如果电路包括电感 和电容,则需要微分方程。 ▼ 3

●电源变换 根据电压源和电流源的定义,此公式成立」 电压电源维持相同的电压,而不管电流如 之所以要进一步详细讨论电源,存在以下 何。这样.输出阻抗为0(山,R=2R要求 两个重要原因。第一个原因是要想掌握分 R=O)。同样,电流电源的输出阻抗无穷大 析技巧,必须更好地理解电源。第二个原 (或未定义),这是因为可以对电流电源输 因是不可能总是能够找到所需的电源,因 入任何电压仍可获得相同的电流。 此必须能够轻松地变换为现有的某种电源」 其中:V=R或I=V/R. 尤其是电流电源比电压电源更难以实现。 ·叠加 在任何包含多个独立电源的线性电路中 压电源,需将其余电源短路:对于电流电 可通过分别计算各个电源的响应(对于电 源,需将其余电源断路)来计算总响应。 P变换 常用转换函数H(s)的基础是拉普拉斯变换 您可以从网上下载或从讲述该主题的大多 F(d()) d(1)e-joidt 以下两种变换对于电子学计算非常重要。 数文章中找到常用拉普拉斯变换表。 拉普拉斯变换是滤波器设计和频率响应计 s域方程式可轻松转换为z域方程式(DSP 脉冲的傅立叶变换在所有频率上提供常量 算的理论基础。傅立叶变换可用来在频域 操作的基本描述符)。 振幅激励。因此.您可以观察该响应,然 中检查时域波形。这些变换主要用于确定 系统的变换函数,有时也会交替使用。傅 后确定变换函数。 立叶变换的优势在于:某些情况下可以进 欧拉恒等式一欧拉恒等式说明了虚平面内 将重复波形简化到2π周期内: 行数字计算。 极坐标和直角坐标的关系 拉普拉斯变换一拉普拉斯变换创建一个单 ej0 cos(0)+isin() 于(x)Fa0+】 n=1 独的数据空间(通常称为$域)来操作函 数。在电子学中,这些函数表示可实现的 解释定义傅立叶分析的公式时,此恒等式 此处 电路。此变换的定义是: 非常有用。 40 Y(s)= -st y(t)di 傅立叶变换一傅立叶变换在操作上与拉普 a0 2 F(x)dx 0 拉斯变换类似。但是,与拉普拉斯变换不 同的是,傅立叶变换可用于重复信号。傅 使用此变换来处理积分和微分非常简单 立叶变换证明:无论何种形状的波形,都 an= F(x)cos(nx)dx 因此该变换常用来分析包含电感和电容的 可将其描述为不同频率、不同振幅的正弦 π 电路。 波的和。要精确地描述非重复性波形,需 示例: 要连续频率带宽上正弦波(以便积分)的 6n=- F(x)sin(nx)dx 1 无穷和。要精确地描述重复波形,需要按 -π Y(s)= 离散频率间隔(以便进行求和)取样的正 s+a 弦波的无穷和。尽管每种情况都需要正弦 后面的方程式主要说明重复波形可以表示 使用以下方程式定义一个指数式衰减: 波的无穷和才能达到绝对精确,但是通常 为许多正弦函数的和。正弦项和余弦项在 情况下,有限的傅立叶项决定了波形的行 相移处有效地创建了一个函数,因此可以 y(t)=e-al 为.并且经常出现其中某些项等于零。因 用多种方式表达该方程式。如果将欧拉恒 此。仅考虑“相关”傅立叶项,也可能得 等式应用到傅立叶变换,那么傅立叶变换 出有用的近似值。系统的有限带宽决定了 将展开为一系列正弦项和余弦项,从中可 此处Q是波形的时间常数。 某些可能项将是非相关项,因为它们超出 找到傅立叶级数的共性。 转换到s域后。电路以零点/极点的形式表 了带宽。傅立叶变换的定义是 H(①)变换函数应该是德立叶函数。比较 示。各方程式的根是相应元件的3dB角 Hs和H())的定义.可发现它们在所有 的位置。虚根可能会导致振荡。 常见的电子应用中都是类似的。 。频率响应(波德图) 与相位。零点处有几条向上倾斜的斜线.并 目了然。直线斜率为20dB/decade·极点或 在频率为3dB处出现转折点。极点向下。 零点的指数。20dB/decade=6dB/octave. 波德图采用拉普拉斯或傅立叶变换函数,在 这些图形重叠在dB一对数频率图和线性相 图中以频率的函数这一形式显示预计的幅度 位一对数频率图上时.整个变换函数将一 版权所有分2OO4,Troi成c.保留所有权利。l地0位产品受美国和外国专利权{包括已取得的和正在中请的专利】的保护,TEKTRO和TBK是ont比nc.的注 一商标,用的其也所青商标名徐均为位]各白公已的务标志。商标或注卧商标。 O04DWBTC-17276-0 Tektronix Enabling Innovation
电源变换 之所以要进一步详细讨论电源,存在以下 两个重要原因。第一个原因是要想掌握分 析技巧,必须更好地理解电源。第二个原 因是不可能总是能够找到所需的电源,因 此必须能够轻松地变换为现有的某种电源。 尤其是电流电源比电压电源更难以实现。 其中:V=IR 或 I=V/R。 根据电压源和电流源的定义,此公式成立。 电压电源维持相同的电压,而不管电流如 何。这样,输出阻抗为 0(I1R = I2R 要求 R=0)。同样,电流电源的输出阻抗无穷大 (或未定义),这是因为可以对电流电源输 入任何电压仍可获得相同的电流。 ▼ 版权所有 © 2004, Tektronix, Inc. 保留所有权利。Tektronix 产品受美国和外国专利权(包括已取得的和正在申请的专利权)的保护。TEKTRONIX 和 TEK 是 Tektronix, Inc. 的注 册商标。引用的其他所有商标名称均为他们各自公司的服务标志、商标或注册商标。 09/04 DM/BT 3GC-17276-0 叠加 在任何包含多个独立电源的线性电路中, 可通过分别计算各个电源的响应(对于电 压电源,需将其余电源短路;对于电流电 源,需将其余电源断路)来计算总响应。 ▼ 变换 以下两种变换对于电子学计算非常重要。 拉普拉斯变换是滤波器设计和频率响应计 算的理论基础。傅立叶变换可用来在频域 中检查时域波形。这些变换主要用于确定 系统的变换函数,有时也会交替使用。傅 立叶变换的优势在于:某些情况下可以进 行数字计算。 拉普拉斯变换 - 拉普拉斯变换创建一个单 独的数据空间(通常称为 s 域)来操作函 数。在电子学中,这些函数表示可实现的 电路。此变换的定义是: 使用此变换来处理积分和微分非常简单, 因此该变换常用来分析包含电感和电容的 电路。 示例: 使用以下方程式定义一个指数式衰减: 此处 是波形的时间常数。 转换到 s 域后,电路以零点/极点的形式表 示。各方程式的根是相应元件的 -3 dB 角 的位置。虚根可能会导致振荡。 常用转换函数 H(s) 的基础是拉普拉斯变换。 您可以从网上下载或从讲述该主题的大多 数文章中找到常用拉普拉斯变换表。 s 域方程式可轻松转换为 z 域方程式(DSP 操作的基本描述符)。 欧拉恒等式 - 欧拉恒等式说明了虚平面内 极坐标和直角坐标的关系: 解释定义傅立叶分析的公式时,此恒等式 非常有用。 傅立叶变换 - 傅立叶变换在操作上与拉普 拉斯变换类似。但是,与拉普拉斯变换不 同的是,傅立叶变换可用于重复信号。傅 立叶变换证明:无论何种形状的波形,都 可将其描述为不同频率、不同振幅的正弦 波的和。要精确地描述非重复性波形,需 要连续频率带宽上正弦波(以便积分)的 无穷和。要精确地描述重复波形,需要按 离散频率间隔(以便进行求和)取样的正 弦波的无穷和。尽管每种情况都需要正弦 波的无穷和才能达到绝对精确,但是通常 情况下,有限的傅立叶项决定了波形的行 为,并且经常出现其中某些项等于零。因 此,仅考虑“相关”傅立叶项,也可能得 出有用的近似值。系统的有限带宽决定了 某些可能项将是非相关项,因为它们超出 了带宽。傅立叶变换的定义是: 脉冲的傅立叶变换在所有频率上提供常量 振幅激励。因此,您可以观察该响应,然 后确定变换函数。 将重复波形简化到 2π 周期内: 此处: 后面的方程式主要说明重复波形可以表示 为许多正弦函数的和。正弦项和余弦项在 相移处有效地创建了一个函数,因此可以 用多种方式表达该方程式。如果将欧拉恒 等式应用到傅立叶变换,那么傅立叶变换 将展开为一系列正弦项和余弦项,从中可 找到傅立叶级数的共性。 H ( ) 变换函数应该是傅立叶函数。比较 H(s) 和 H ( ) 的定义,可发现它们在所有 常见的电子应用中都是类似的。 ▼ 频率响应(波德图) 波德图采用拉普拉斯或傅立叶变换函数,在 图中以频率的函数这一形式显示预计的幅度 与相位。零点处有几条向上倾斜的斜线,并 在频率为 -3 dB 处出现转折点。极点向下。 这些图形重叠在 dB - 对数频率图和线性相 位 - 对数频率图上时,整个变换函数将一 目了然。直线斜率为 20 dB/decade * 极点或 零点的指数。20 dB/decade = 6 dB/octave。 ▼