
动态电路的相量分析法和 $域分析法 第十二章 拉普拉斯变换在电路分析中的应用 (S域分析法)
第十二章 拉普拉斯变换在电路分析中的应用 ( S域分析法) 动态电路的相量分析法和 s域分析法 1

§12-1拉普拉斯变换及其几个基本性质 时间函数f八)的拉普拉斯变换记为f()]其定义为 罗[f)]=f)e"ed (12-1) -[R)e-"de 其中s=σ+jw称为复频率,积分限0_和是固定的,所以积分的结果与t无 关,而只取决于5,即复频率s的函数,记为 孔f()]=F(s) (12-2) F(s)即为函数f()的拉普拉斯变换。在电路中用U(s)和(s)分别表示u(t)和 (:)的拉普拉斯变换。拉普拉斯变换以后简称拉氏变换。 运用拉普拉斯(Laplace)变换,简称拉氏变换进 行动态电路的分析方法称为拉氏变换法或复频 率域(S域)分析法。 2
§12-1 拉普拉斯变换及其几个基本性质 2 运用拉普拉斯(Laplace)变换,简称拉氏变换进 行动态电路的分析方法称为拉氏变换法或复频 率域(S域)分析法
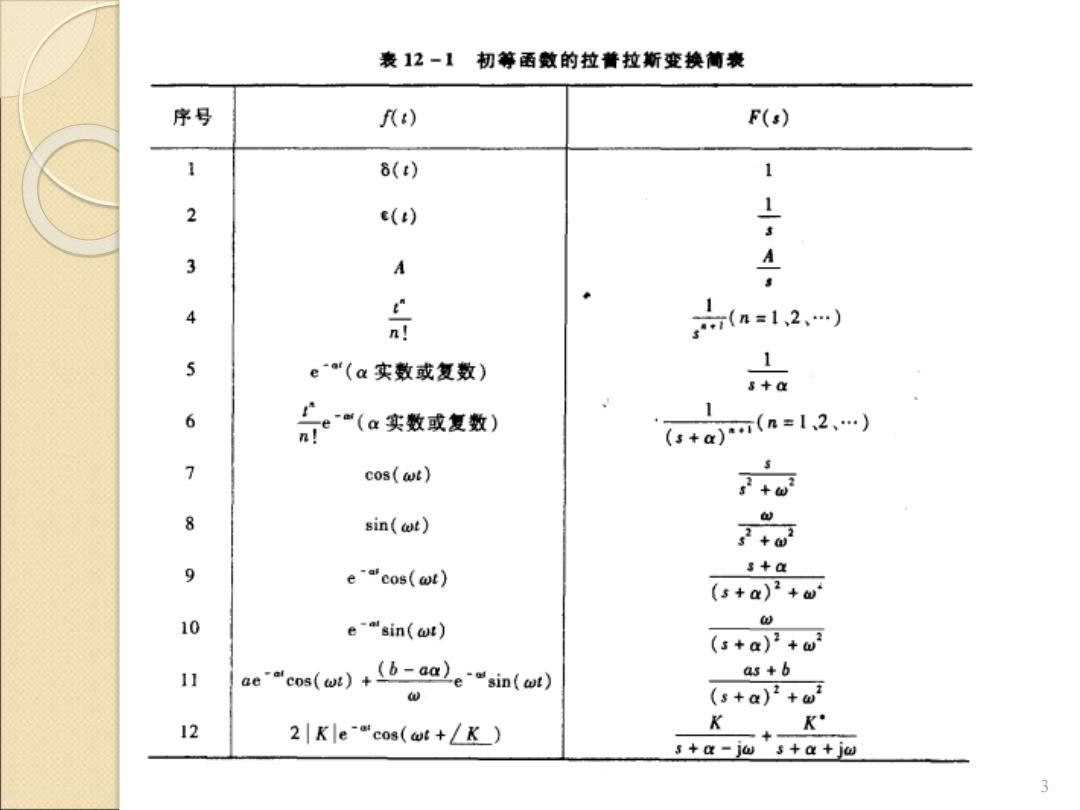
表12-1初等函数的拉普拉斯变换葡表 序号 R) F(s) 8(t) 1 2 e() L 3 A A a12 5 e“(a实数或复数) s+a 6 ne“(a实数或复数) (s+am(n=12、…) 1 7 cos(wt) +0 8 sin(wt) 2+0 9 e-"cos(wt) 3+a (s+a)2+如 10 e-sin(wt) u (s+a)2+w 11 ae"eos(ur)+b-aale“sin(l) as +b (s+a)2+0 12 2Kle-"cos(wt+/K) K K' s+a-jo s+a+jw 3
3

Laplace变换的性质 线性性质若罗{f(t)}=F,(s),k=1、2,则对任何常数a,和α2(实数或 复数) af()+a5(t)]=a[f()门]+a,(t)] =aF,(s)+a2F2(s) 微分性质 若 [f(t)]=F(s) 则 才期=F(s)-0.) 积分性质 若 [f(t)]=F(s) 则 af Red]-F() 4
Laplace变换的性质 4

§12-2电路的S域模型 一、基尔霍夫定律的s域变换 时域中有:∑i(t)=0,∑u(t)=0 如果I(s)U(s)分别为i(tu(t)的Laplace变换,则 由Laplace变换的线性性可得: ∑1(s)=0及∑U(s)=0。 5
§12-2 电路的S域模型 5 一、基尔霍夫定律的s域变换 = = = = 及 。 由 变换的线性性可得: 如果 、 分别为 、 的 变换,则 时域中有: ( ) 0 ( ) 0 Laplace ( ) ( ) ( ) ( ) Laplace ( ) 0, ( ) 0 I s U s I s U s i t u t i t u t
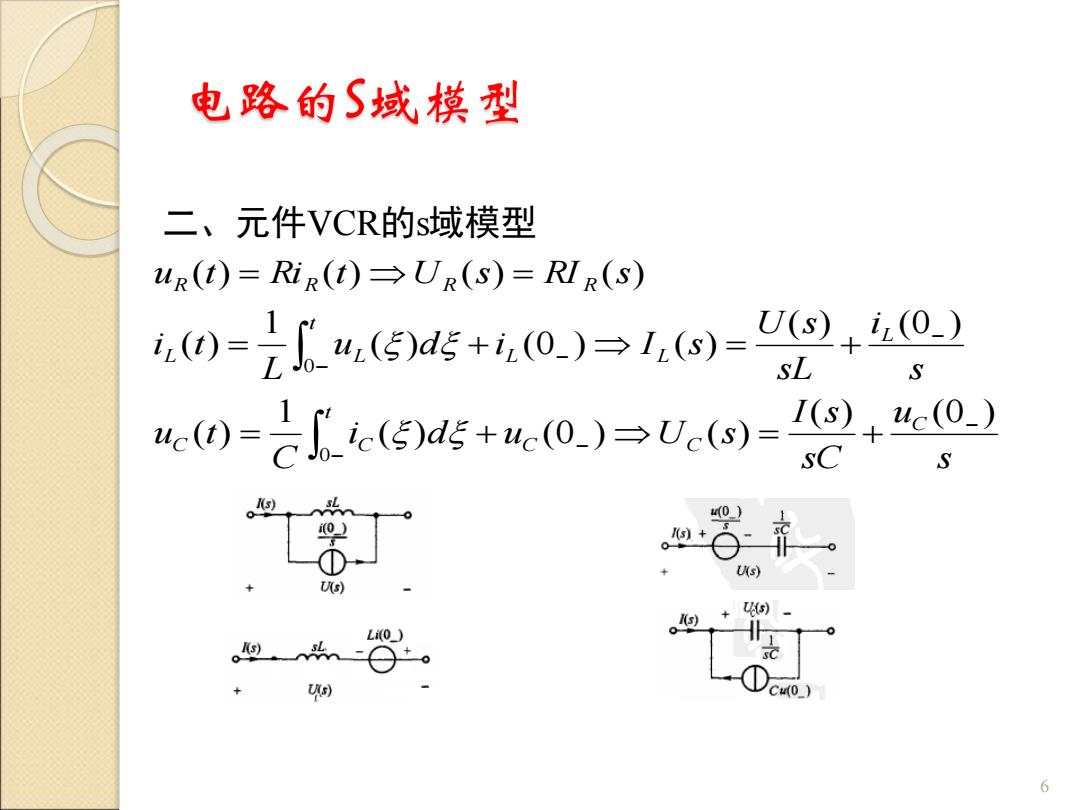
电路的S域模型 二、元件VCR的s域模型 uR(t)=RiR(t)UR(S)=RIR(s) 40=4,(5)d5+,0.)→1,(s)= U(s)iz(0_) sL S 4.0=己e(5)d5+4:0.)→U(s)= 1(s) 4c(0_) sC S 0) ① U(s) U(s) U(s) L0_) ) C40) 6
电路的S域模型 6 二、元件VCR的s域模型 − − − − − − = + = + = + = + = = t C C C C C t L L L L L R R R R s u sC I s i d u U s C u t s i sL U s u d i I s L i t u t Ri t U s RI s 0 0 ( ) (0 ) ( ) (0 ) ( ) 1 ( ) ( ) (0 ) ( ) (0 ) ( ) 1 ( ) ( ) ( ) ( ) ( )

运用s域模型求解电路的步骤 ① 把电路变量变换为相对应的Laplace变换形式,建 立电路的s域模型 ② 就s域模型对电路进行分析,得到s域下电路的解 ③ 求s域解的反Laplace变换,得到对应的时域解表达 式。 7
运用s域模型求解电路的步骤 ① 把电路变量变换为相对应的Laplace变换形式,建 立电路的s域模型 ② 就s域模型对电路进行分析,得到s域下电路的解 ③ 求s域解的反Laplace变换,得到对应的时域解表达 式。 7

例题 求图(a)所示RC电路在阶跃输入下的响应Uc(t)。 (a) (b) 1)做出电路的s域模型 2)由s域模型及基尔霍夫定律得: I(s)R+(s) c(0)=A sC S S A uc(O_) ..I(5)=s S 1 R+ sC 8
例题 ❖ 求图(a)所示RC电路在阶跃输入下的响应UC(t)。 8 1)做出电路的s域模型 sC R s u s A I s s A s u sC I s I s R C C 1 (0 ) ( ) ( ) (0 ) ( ) 2) s + − = + + = − − 由 域模型及基尔霍夫定律得:

E(t) 0) (a) (b) A uc(0) =20 uc(0_) sC SC 1 R+- S 1A-uc(0_),uc(0_ 2=A A uc(0_) S SCR+1 S S s+1/RC s+1/RC 3)求反变换 a 9
9 s RC u s RC A s A s u sCR A u s s u sC R s u s A s sC u sC I s U s C C C C C C 1/ (0 ) 1/ (0 ) 1 1 (0 ) (0 ) 1 (0 ) ( ) (0 ) 1 ( ) + + + + = − + − = + + − = + = − − − − − − (1 ) (0 ) ( ) ( ) (0 ) ( ) 3) / / / / A e u e t u t A Ae u e t t R C C t R C t R C C t R C C − − − − − − = − + = − + 求反变换

§12-3零状态分析 若初始条件为零,则s域模型下的电阻、电容、电感 的VCR简化为: uR(t)=RiR(t)UR(S)=RIR(S) ,0=元4,(5)d5→1,(s)= U(s) sL 4e0=乙e(5d5→U.()= I(s) sC s 0 U(s) U(s) U (a) (b) 图零状态元件的城模型 10
§12-3零状态分析 ❖ 若初始条件为零,则s域模型下的电阻、电容、电感 的VCR简化为: 10 − − = = = = = = t C C C t L L L R R R R sC I s i d U s C u t sL U s u d I s L i t u t Ri t U s RI s 0 0 ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( )