
第六章 一阶电路 2018年11月19日
第六章 一阶电路 2018年11月19日 1

动态电路 ?在动态电路中,各支路电流和各支路电压都分别受 KCL和KVL的约束,只是在动态电路中,来自元件 性质的约束,除了电阻元件和电源元件的VAR外, 还有电容和电感等动态元件的VAR。 只含一个动态元件的线性、时不变电路,用线性常 系数一阶常微分方程来描述,用一阶微分方程来描 述的电路称为一阶电路。 2
动态电路 ❖ 在动态电路中,各支路电流和各支路电压都分别受 KCL和KVL的约束,只是在动态电路中,来自元件 性质的约束,除了电阻元件和电源元件的VAR外, 还有电容和电感等动态元件的VAR。 ❖ 只含一个动态元件的线性、时不变电路,用线性常 系数一阶常微分方程来描述,用一阶微分方程来描 述的电路称为一阶电路。 2

§6-1分解方法在动态电路分析中运用 一 阶电路可看成由两个单口网络组成,其一含所有 的电源及电阻元件,另一个含一个动态元件。 必 以图(b),含源电阻网络部分N,用戴维南定理或诺顿 定理化简后,电路将如图(b)或(c)所示。 由图(b)或(c),可以求得单口网络的端口电压,亦即 电容电压uco R 含源电 4c(0卡Cisc uc(t) 阻网络 (a) (b) (c) 3
§6-1分解方法在动态电路分析中运用 ❖ 一阶电路可看成由两个单口网络组成,其一含所有 的电源及电阻元件,另一个含一个动态元件。 ❖ 以图(b),含源电阻网络部分N1用戴维南定理或诺顿 定理化简后,电路将如图(b)或(c)所示。 ❖ 由图(b)或(c),可以求得单口网络的端口电压,亦即 电容电压uc。 3

一阶电路方程 由KVL可得 un(t)+uc(t)=uoc (t) “因=R.0=c能 RC duc+Gouc isc(t) C dt 同理,对电感ur(t)+4(d)=uoc(t) ur(t)=R,(d),1 0=1 Li+Ri uoc (t) dt +i,=ic() GoL dt 4
一阶电路方程 由KVL可得 4 同理,对电感 ( ) ( ) ( ) ( ) ( ) ( ) ( ) G u i (t) dt du C u u t dt du R C dt du u t R i t i t C u t u t u t o C SC C C OC C o C R o R C OC o o + = + = = = + = , ( ) ( ) ( ) ( ) ( ) ( ) ( ) i i (t) dt di G L R i u t dt di L dt di u t R i t u t L u t u t u t L SC L O o L OC L L R o L L R L OC o o + = + = = = + =

电路的状态方程 冬电容电压和电感电流称为电路的状态变量,因而方程 式称为电路的状态方程。 冬若以x泛指状态变量,w泛指电路的输入,则状态方 程可归结为下列的标准形式: =Ax+Bw c dt 对电容 duc=- dt 对电感 d=- d 必状态方程本身体现了电路状态演变的情况,即状态 的变化率是当前状态和当前输入的函数。 5
电路的状态方程 ❖ 电容电压和电感电流称为电路的状态变量,因而方程 式称为电路的状态方程。 ❖ 若以x泛指状态变量,w泛指电路的输入,则状态方 程可归结为下列的标准形式: 5 Ax Bw dt dx = + 对电容 ( ) i (t) L R i L R dt di u t R C u dt R C du s c o L L o oc o C o C = − + = − + 1 1 对电感 ❖状态方程本身体现了电路状态演变的情况,即状态 的变化率是当前状态和当前输入的函数

§6-2零输入响应 冬电路在没有外加输入时的响应称为零输入响应。零输 入响应仅仅是由非零初始状态所引起的,是由初始时 刻电容中电场的贮能或电感中磁场的贮能所引起的。 ÷如果在初始时刻贮能为零,那么在没有电源作用的情 况下,电路的响应也为零。 i(t) RoI, (a) (b) (c) 6
§6-2 零输入响应 ❖ 电路在没有外加输入时的响应称为零输入响应。零输 入响应仅仅是由非零初始状态所引起的,是由初始时 刻电容中电场的贮能或电感中磁场的贮能所引起的。 ❖ 如果在初始时刻贮能为零,那么在没有电源作用的情 况下,电路的响应也为零。 6
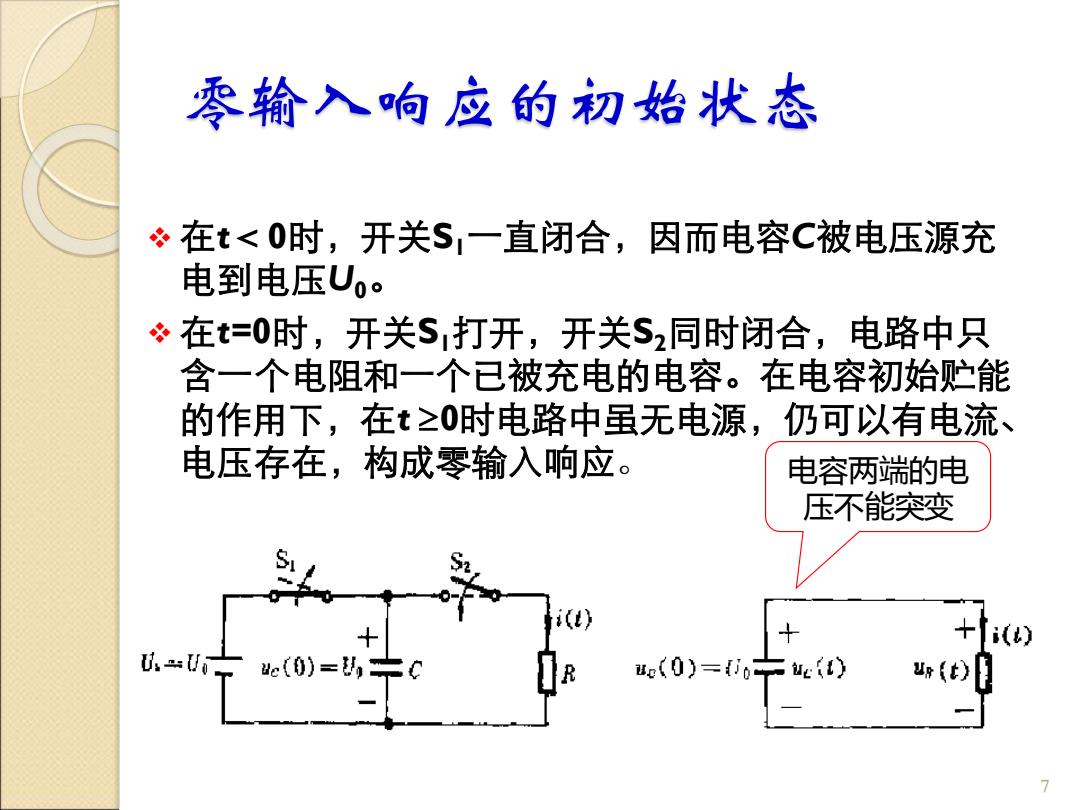
零输入响应的初始状态 在t<0时,开关S,一直闭合,因而电容C被电压源充 电到电压Uo。 在t=0时,开关S打开,开关S2同时闭合,电路中只 含一个电阻和一个已被充电的电容。在电容初始贮能 的作用下,在t≥0时电路中虽无电源,仍可以有电流、 电压存在,构成零输入响应。 电容两端的电 压不能突变 i() U-=U0 c(0)=, 7
零输入响应的初始状态 ❖ 在t<0时,开关S1一直闭合,因而电容C被电压源充 电到电压U0。 ❖ 在t=0时,开关S1打开,开关S2同时闭合,电路中只 含一个电阻和一个已被充电的电容。在电容初始贮能 的作用下,在t 0时电路中虽无电源,仍可以有电流、 电压存在,构成零输入响应。 7 电容两端的电 压不能突变

零输入响应的状态方程 必如果关心的是t>0时电路的情况,则电路方程为: RC ducuc =0 t≥0 dt ?根据电容电压的参考方向,结合初始电压U,的实际方 向,uc可记为 uc(t)=Ke Rc 解得 uc(O)=K=U。 uc(t)=Une Rc' t≥0 1 式中 RC 为特征方程 RCS+1=0的根。 8
零输入响应的状态方程 ❖ 如果关心的是t>0时电路的情况,则电路方程为: ❖ 根据电容电压的参考方向,结合初始电压U0的实际方 向,uC可记为 8 式中 解得 + u = 0 t 0 dt du RC C C ( ) ( ) ( ) 1 0 1 0 0 1 0 0 1 + = − = = = = − − RCS RC u K U u t U e t u t Ke t RC C C t RC C 为特征方程 的根
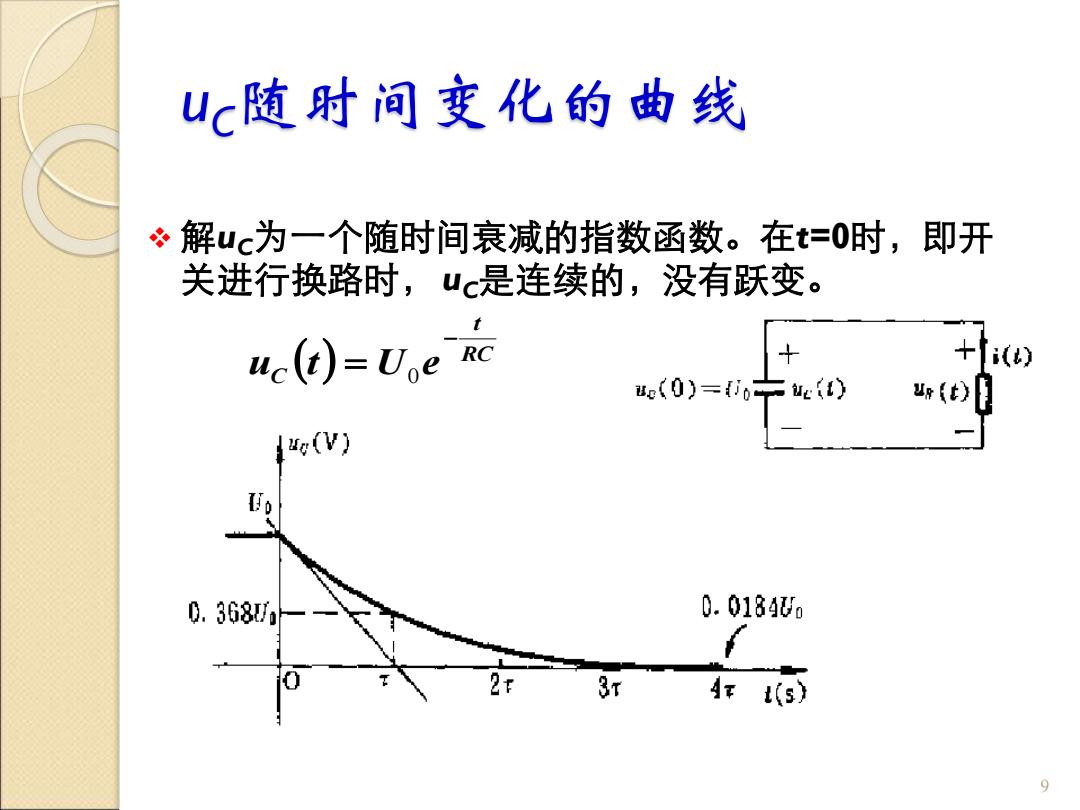
u(随时间变化的曲线 ?解uc为一个随时间衰减的指数函数。在t=O时,即开 关进行换路时,uc是连续的,没有跃变。 uc(t)=Uoe RC +() e(0)=i0—e1) {to0 {e(V) 0.368 0.0184W0 3T 4π(s)
uC随时间变化的曲线 ❖ 解uC为一个随时间衰减的指数函数。在t=0时,即开 关进行换路时, uC是连续的,没有跃变。 9 ( ) RC t C u t U e − = 0
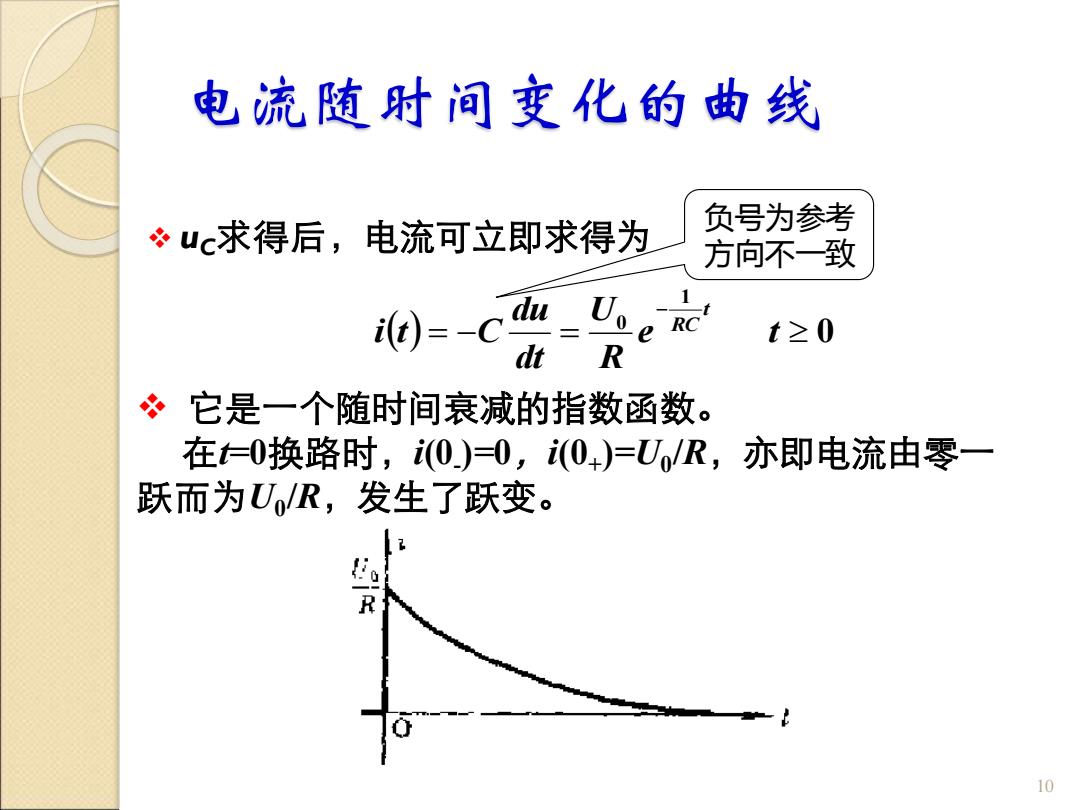
电流随时间变化的曲线 ?uc求得后,电流可立即求得为 负号为参考 方向不一致 1 i(t)=-C du t≥0 R 冬它是一个随时间衰减的指数函数。 在=0换路时,0)=0,(0)=U/R,亦即电流由零一 跃而为U/R,发生了跃变。 10
电流随时间变化的曲线 ❖ uC求得后,电流可立即求得为 10 ( ) 0 1 0 = − = − e t R U dt du i t C t RC ❖ 它是一个随时间衰减的指数函数。 在t=0换路时,i(0- )=0,i(0+ )=U0 /R,亦即电流由零一 跃而为U0 /R,发生了跃变。 负号为参考 方向不一致